中国雾霾污染的空间计量分析

林楚海

（暨南大学 经济学院，广州 510000）

0 引言

雾霾，即雾和霾的组合词。雾是由大量悬浮在近地面空气中的微小水滴或冰晶组成的气溶胶系统，而霾是指由于灰尘、硫酸、硝酸、有机碳氢化合物等粒子悬浮在空气中，而使水平能见度小于1000米一种现象。雾霾天气主要由空气中的二氧化硫、氮氧化物和可吸入颗粒物这三项引起，它们与雾气结合在一起，会让天空瞬间变得阴沉灰暗，也对人体和社会带来各方面的影响。2014年，中国31个省份中，PM10年平均浓度达到国家一级标准的只有海南省，而SO2达到国家一级标准的也只有7个省份，从整体上看，雾霾污染依然不容乐观。再加上雾霾的源头多种多样，比如汽车尾气、工业排放、建筑扬尘、垃圾焚烧等，因此，如何在众多因素中快速找到造成雾霾的主导因素并采取有效的治理措施，成为中国政府和居民急需解决的难题。基于此，本文将选取中国31个省份2014年三种雾霾主要组分——PM10、SO2、NO2的年平均浓度作为目标变量，并利用LASSO高维变量选择方法从22个社会影响因子中筛选出非零变量进行空间回归分析，从而揭示中国内地雾霾污染的真正来源和空间影响因素。

1 研究方法

1.1 空间计量分析

1.1.1 空间权重矩阵

空间权重矩阵即地理单元间的空间结构关系的一种表达形式，描述了各单元间的邻近关系。空间权重矩阵W一般表示为一个n维矩阵，其基本形式可表示如下：

其中，wij表示区域i和j的邻近关系，一般分为基于邻近概念的空间权重矩阵和基于距离的空间权重矩阵。其定义如下：

1.1.2 全局空间自相关

全局空间自相关描述的是研究范围内所有单元之间的整体空间关系。一般采用Moran’s I统计量来描述整个研究区域上所有空间单元之间的平均关联程度及其显著性。其计算公式如下：

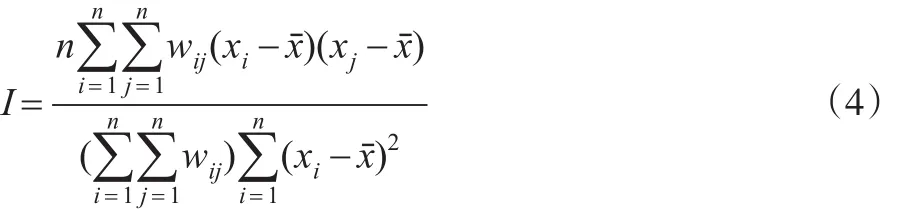
其中，xi表示地区i的观测值，，n为地区数，wij为空间权重矩阵。Moran’s I统计量的取值范围为[-1，1]。I越接近1，表示区域间空间正相关的程度越强；当I越接近-1时，表示区域间空间负相关的程度越强；当I接近0时，则表示区域间不存在空间自相关性。

1.1.3 局域空间自相关

局域空间自相关统计量就是用来识别随空间位置不同而存在的不同空间关联模式，从而观察空间局部不平稳性。本文的局域空间自相关分析将采用局部Moran’s I指数绘制的集聚地图和显著性地图。

局部Moran’s I指数的计算公式如下：

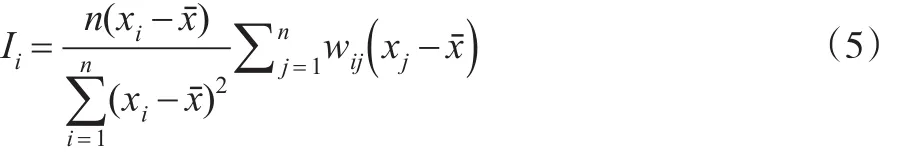
其中，Ii表示i地区与其相邻区域之间的空间相关程度，其他符号的含义同式（4），这里不再赘述。当Ii＞0时，表示第i个地区某种属性值与其周围地区的属性值呈空间正相关，表现为高高集聚或低低集聚；当Ii＜0时表示负相关，表现为高低集聚或低高集聚。

1.1.4 空间回归分析

（1）空间滞后模型：假定空间变量的空间依赖性仅通过因变量产生，即某一空间对象上的因变量不仅与同一对象上的自变量有关，还与相邻对象的因变量有关，其形式为：

其中，y为n×1阶截面数据被解释变量，W为空间权重矩阵，Wy即为被解释变量的空间滞后向量，其系数ρ为空间自回归系数，反映了相邻区域对本区域的作用，当ρ显著时，说明因变量间存在明显的空间依赖性，当ρ＞0时，表明相邻空间区域的空间相互作用表现为“溢出效应”;反之，则表现为“负效应”或“扩散效应”。X即为n×k外生解释变量矩阵，其中k为解释变量的个数。ε为n×1阶随机误差向量。

（2）空间误差模型：在某些情况下，空间依赖可能是某些对局域内多个单元均有影响的遗漏变量造成的，从而造成区域“一损俱损，一荣俱荣”的效果，这时候需要考虑误差项的空间自回归过程。其形式为：

其中，λ是误差项的空间自回归系数，Wε是误差项的空间滞后向量，μ为不相关的、均值为0且同方差的误差项。若λ显著，则说明了邻近区域的关于因变量的误差冲击对本地区的观测值具有显著性影响。

（3）空间通用模型：空间通用模型综合了空间滞后模型和空间误差模型，其形式为：

其中，空间权重矩阵W1与W2可以相同，也可以不同，其他符号含义与上述两个模型相同，这里不再赘述。

（4）空间相关性检验与模型选择：一般可通过两个拉格朗日乘数LMERR、LMLAG及其稳健的R-LMERR、R-LMLAG等统计量来实现。当LMLAG比LMERR显著，且R-LMLAG显著而R-LMERR不显著时，则选择空间滞后模型更为合适；相反地，如果LMERR比LMLAG显著，且R-LMERR显著而R-LMLAG不显著时，则选择空间误差模型更为合适。其他可供参考的模型比较准则还有对数似然值、赤池信息准则（AIC）和施瓦茨准则（SC）等。当对数似然值越大，AIC和SC值越小，则模型拟合效果越好。

1.2 LASSO高维变量选择

设有p个自变量 x1，x2，…，xp和因变量y，并建立如下的线性回归模型：

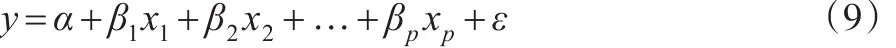
其中，α为常数项，β1，β2，…，βp为自变量的回归系数，ε为随机扰动项。设(xi1，xi2，…，xip;yi)，i=1，2，…，n 为n组观测值，假定数据已经经过中心化和标准化，即，…，βp)T,则 β 的最小二乘估计为：

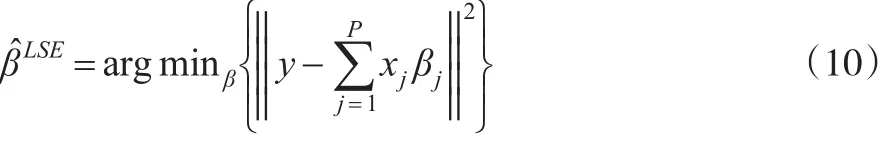
1996年，Tibshirani提出了LASSO变量选择方法，其基本思想是在最小二乘的基础上施加l1惩罚项，将一些变量的系数恰好压缩为零，从而实现变量选择。其表达式如下：

其中，s≥0是一个惩罚参数，控制着压缩的程度，s越小，压缩程度越强，会有更多的系数被压缩至零。记最小二乘估计得到的参数估计为实现压缩，即有些系数会变为0，这些等于0的变量就会被删除，从而达到变量选择的目的。其等价形式如下：

若设计阵正交，即XTX=I，LASSO的参数估计为：

2 实证分析

2.1 数据说明

本文选取中国31个省份2014年的PM10、SO2、NO2的年平均浓度（微克/立方米）作为被解释变量，同时从产业结构、人口因素、固定资产投资和房地产、能源因素、城市建设五个大方面选择22个指标作为自变量，数据均来源于各省2015年的《统计年鉴》和《环境统计公报》，如下页表1所示。

采用ArcGis 10.0软件计算空间权重矩阵，相邻规则采用Rook相邻。另外，由于海南岛远离陆地，与其他省份没有边界相邻，为了避免出现“孤岛”现象，将邻居个数最低值设为1，从而使得每个省份至少都有一个邻居相邻。

表1 指标含义与说明

2.2 全局空间自相关分析

通过Geoda软件进行全局空间自相关分析，得到31个省份2014年的PM10、SO2、NO2年平均浓度对应的全局Moran’s I指数，如表2所示。结果表明，PM10、SO2、NO2年平均浓度对应的全局Moran’s I指数分别为0.5377、0.3501、0.5044，并且对应的P值均小于0.05，说明31个省份之间的PM10、SO2、NO2的空间自相关性非常显著，且呈正的空间自相关，而非完全随机分布。

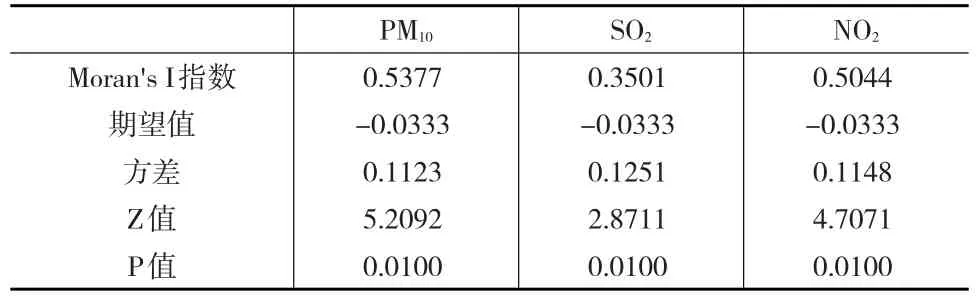
表2 全局Moran’s I指数及相关统计指标

2.3 局域空间自相关分析

在现实中，各地区雾霾组分受到的空间影响的模式完全一致一般是很少见的，为了进一步探究各省份与相邻省份之间的空间影响关系，本文绘制了各省份PM10、SO2、NO2的显著性地图和聚类地图（图略）。在0.05的显著性水平下，华北地区的北京、天津、山西、河北以及华东地区的山东、华中地区的河南这六个省份的PM10年平均浓度具有显著性的空间正自相关，呈“高高集聚”的分布形态；而华南地区的广东、广西和西南地区的云南、贵州的PM10年平均浓度也具有显著性的正自相关，但呈“低低集聚”的分布形态。其他省份的PM10年平均浓度的空间自相关性则不显著，呈随机分布的形态。可以发现，中国PM10的高浓度聚集区主要分布在华北地区以及华东、华中地区的个别省份，这几个地区是中国人口较为密集和工业生产较为频繁的地区，工业气体废弃物的排放和众多人口冬季的采暖燃煤可能是造成这几个地区PM10浓度高的主要原因。

对于SO2来说，山东、河北、河南这三个省份的SO2年平均浓度具有显著性的空间正相关关系，呈现“高高集聚”的空间布局。而北京和内蒙古虽然都与高SO2的河北相邻，但却均呈现出“低高集聚”，对于北京来说，这可能与政府近几年的污染治理息息相关，SO2是与燃煤直接相关的大气污染物。自1998年以来，在燃煤锅炉清洁能源改造上，北京城六区累计完成约5.13万蒸吨燃煤锅炉改造，基本实现了城六区无燃煤锅炉，因此，北京的SO2年平均浓度才能在高SO2的相邻区域下保持较低的浓度，也从侧面反映出工业污染治理对环境带来的巨大效应。而对于内蒙古来说，其SO2年平均浓度之所以能保持较低的浓度，可能与其地理优势有关，内蒙古北有大青山、东南部有蛮汉山、西南及南部则为平原，且由东北向西南逐渐倾斜，因此，形成了阻碍SO2扩散的低气压带，对河北的SO2的空间传输形成了较强的阻碍作用。而广东属于沿海省份，海陆风对雾霾组分的扩散和稀释起了很大的作用，再加上自身污染没有北方省份严重，因此，其SO2年平均浓度依然呈现“低低集聚”，即与周围省份相似，SO2年平均浓度都相对较低。

另外，北京、天津、河北三省的NO2年平均浓度呈现“高高集聚”的分布形态，说明这三个省份也是NO2的高浓度地区，而广东的NO2年平均浓度则相对较低，呈“低低集聚”分布。

2.4 基于LASSO方法的变量选择

由全局空间自相关分析和局域空间自相关分析可以发现，中国各省份之间的雾霾组分确实存在空间效应，因此，需要对其进行空间回归分析，以探讨哪种回归模型更适合于三种雾霾组分。在建模之前，先使用LASSO方法对变量进行筛选，以使得模型更加简洁和更有解释性。为了消除各变量量纲的影响，先对各变量取对数，其中，X1(第二产业增加值占GDP比重)、X3(城镇人口比重)、X11(建成区绿化覆盖率)、X15(生活垃圾无害化处理率)、X16(森林覆盖率)由于是百分比的形式，因此不进行对数化处理。然后，对数据进行标准化、中心化处理。最后通过LASSO方法得到各组分的非零变量如下页表3所示。

2.5 空间回归分析

接下来，利用R语言的spdep安装包，根据LASSO筛选出的非零变量对三种雾霾组分分别进行空间回归分析，以探讨最优的拟合模型。

2.5.1 PM10的空间回归分析与检验

建立PM10的回归模型，并进行诊断性检验，结果如表4所示。结果表明，在lnPM10的普通最小二乘估计中，X1、lnX10、X16的回归系数对应的P值均小于0.05，均通过显著性检验。从拉格朗日乘数检验结果来看，LMLAG对应的P值为0.00214，远小于LMERR对应的P值0.12300，而且R-LMLAR的P值为0.00194＜0.05，通过了显著性检验，而R-LMERR的P值为0.10980，在5%的显著性水平下不显著。因此，应该选择空间滞后模型较为合适。从空间滞后模型的拟合效果来看，拟合优度为74.669%，比最小二乘估计的拟合优度（60.470%）高，而且其对数似然值(-23.75857)比最小二乘估计的（-29.09351）大，AIC和SC也比最小二乘估计的小，因此，采用空间滞后模型是最优的，其表达式如下：

表3 LASSO方法筛选出的非零变量

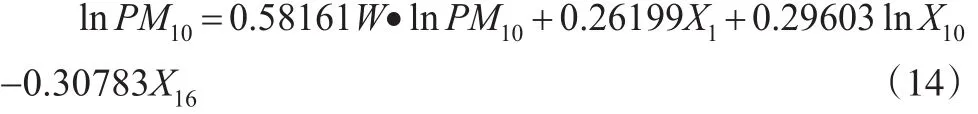
从模型的回归系数来看，各变量依然对PM10具有显著性的影响，并且其空间回归系数ρ=0.582，对应的P值为0.00001，也具有很强的显著性，说明中国各省份之间的PM10浓度具有很强的空间溢出效应，即当空间滞后值每增加1%时，本地的PM10浓度将平均上升0.582%。从社会影响因子来看，当第二产业占GDP比重每上升1%时，PM10的年平均浓度将平均上升0.262%，这说明第二产业的发展对PM10浓度带来了重要的影响。第二产业主要分为工业和建筑业，对于工业来说，其对煤炭、原油等化石燃料的燃烧是该行业产生PM10的主要原因。仅2013年，我国工业煤炭消费总量占煤炭消费总量的比重就已经达到94.99%。因此，第二产业工业越发达的地区，其PM10将可能越高。而建筑业由于对钢筋、水泥的需求比较大，因此，也间接地增加了化石燃料的燃烧，另外，建筑施工过程引起的扬尘也是PM10的主要来源。从天然气的供气量（X10）来看，当天然气供气总量每增加1%时，PM10的年平均浓度将平均上升0.296%，这结果可能与天然气作为一种清洁能源相悖，但从目前我国天然气的用途来看，其用途主要分为城市燃气、化工原料、天然气发电、工业燃料四大块，并且化工原料和工业燃料的用气量占绝大部分。2013年，化工原料和工业燃料的天然气用气量占天然气用气总量的41%。因此，天然气供气总量很大一部分还是用于工业发展，天然气供气总量大的地区，其工业的比重也可能比较高，因此，工业污染对PM10的年平均浓度的影响可能也比较大。而森林覆盖率（X16）与PM10的年平均浓度则呈负相关作用，当森林覆盖率每增加1%时，PM10的年平均浓度将平均下降0.308%，这主要是由于森林对PM10具有滞留、吸附和拦截功能，因此，森林覆盖率越大，PM10的年平均浓度将越低。2.5.2 SO2、NO2的空间回归分析与检验

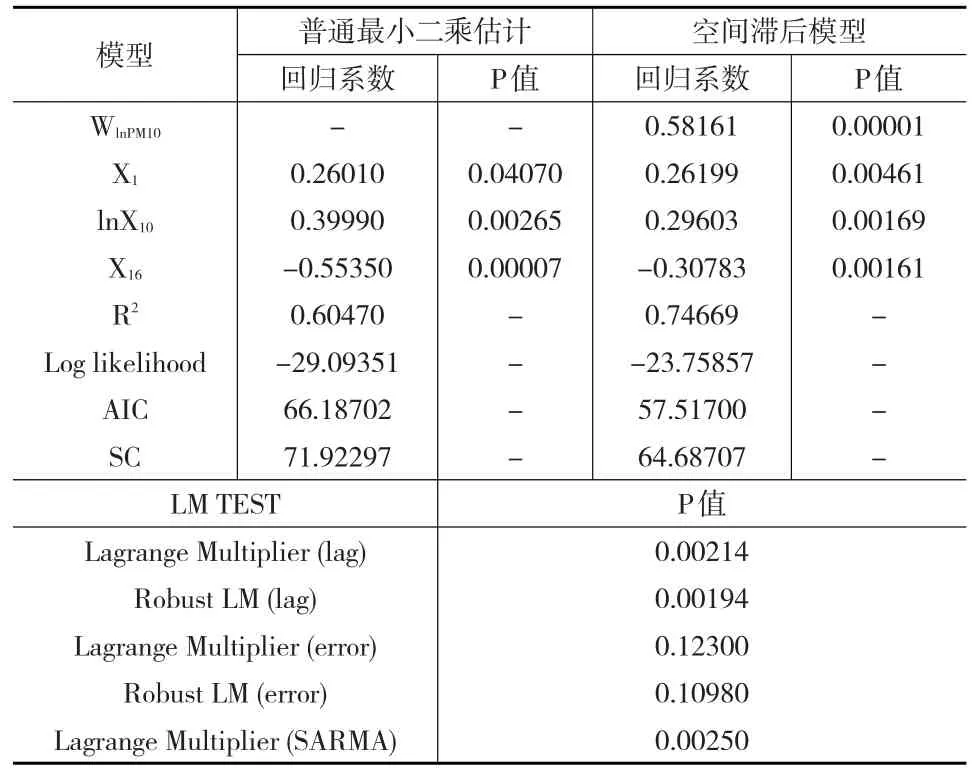
表4 PM10的回归分析与诊断性检验

同理，对SO2、NO2进行空间回归分析，得到下页表5、表6。结果表明，SO2的空间回归模型更适合空间滞后模型，其表达式如式（15）所示；而NO2则没有通过拉格朗日乘数检验，其回归模型使用普通最小二乘估计即可，将不显著变量剔除后，得到修正后的模型结果如式（16）、下页表7所示。从SO2模型中各变量的回归系数和显著性检验来看，在5%的显著性水平下，各变量均通过了显著性检验。在空间区域影响方面，空间回归系数ρ对应的P值为0.00055，说明我国各省份之间的SO2也存在空间溢出效应，并且当空间滞后值每增加1%时，本地的SO2年平均浓度将平均增加0.491%。从社会发展影响来看，SO2年平均浓度与第二产业增加值占GDP的比重呈正相关，当比重每增加1%时，SO2年平均浓度将平均上升0.429%，这说明第二产业增加值所占地区经济的比重越大，其SO2年平均浓度将可能越高，这主要还是由于第二产业中的工业废气的排放巨大。2014年，全国废气中SO2排放量为1974.4万吨，其中，工业SO2排放量为1740.4万吨，所占比重达到88.15%。因此，治理工业废弃项目对雾霾治理至关重要。从治理废弃项目完成投资(X18)的回归系数可以发现，当治理废弃项目完成投资每增加1%时，SO2年平均浓度将平均下降0.270%。另外，森林也有降低SO2浓度的作用，当森林覆盖率每增加1%时，SO2年平均浓度将平均下降0.233%。这主要是由于植物对SO2有吸收作用，可对空气进行净化。而对于NO2，X3（城镇人口比重）和X21（民用汽车拥有量）与NO2年平均浓度呈正相关，城镇人口比重每增加1%，NO2年平均浓度将平均增加0.365%，民用汽车拥有量每增加1%，NO2年平均浓度将平均增加0.503%。从这两个指标可以看出，我国各省份大气中的NO2浓度主要源自城市中汽车尾气的排放，当城市人口比重越大，所拥有的民用汽车数量将越多，其大气中的NO2浓度将越高。此外，与PM10和SO2相似，提高森林覆盖率将是降低NO2浓度一个有效的措施。

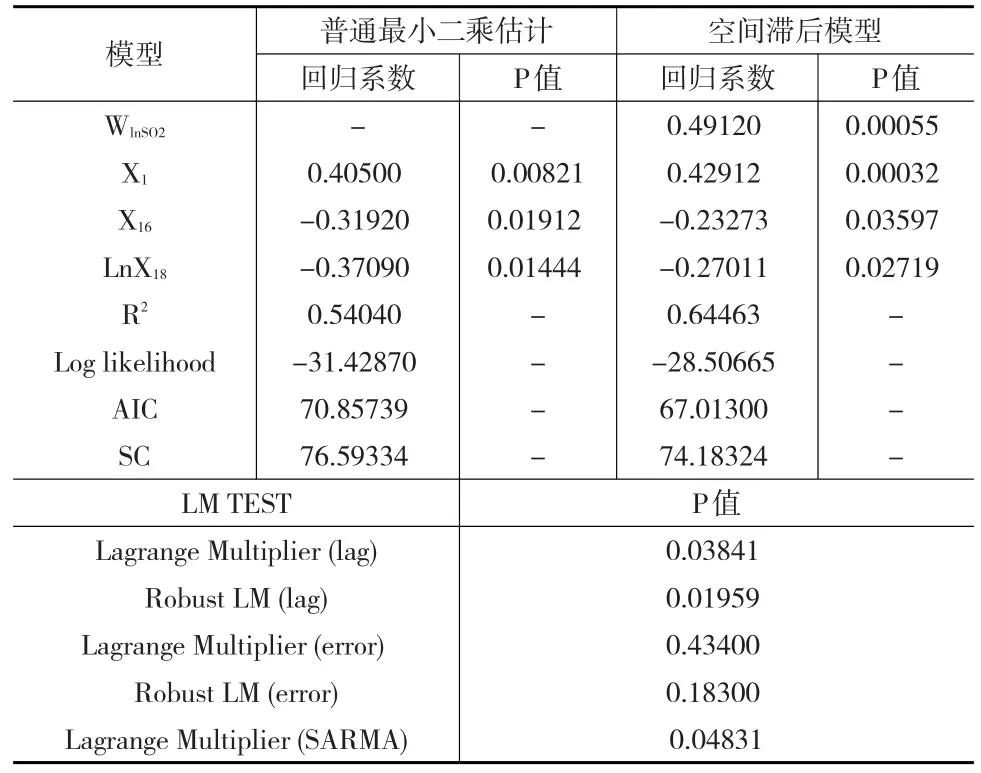
表5 SO2的回归分析与诊断性检验

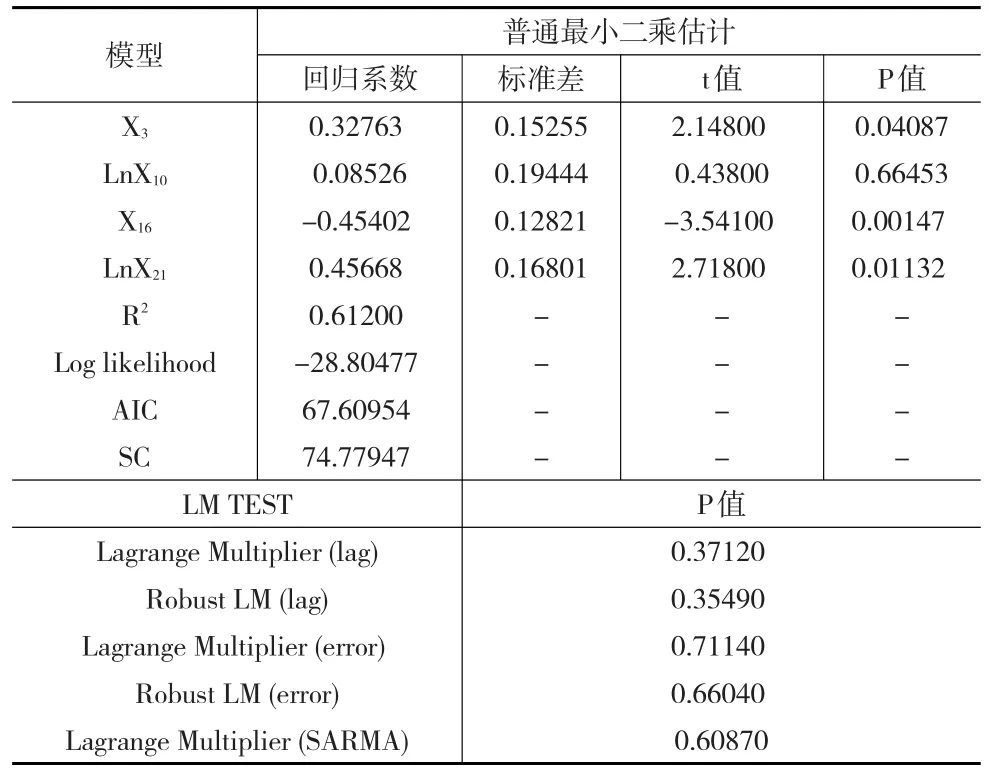
表6 NO2的回归分析与诊断性检验

表7 NO2修正后的回归模型

3 结论

本文通过空间计量分析和LASSO变量选择方法，对中国31个省份造成雾霾天气的三种主要污染物——PM10、SO2和NO2进行研究分析。结果发现：（1）华北地区及其周边雾霾天气最严重，呈“高高集聚”的空间分布。（2）第二产业是空气中PM10和SO2的主要来源，且空间效应显著。第二产业中煤炭等化石燃料的燃烧和废弃项目的排放是PM10和SO2的主要来源，通过治理工业废弃项目完成投资的增加有助于SO2排放的减少。另外，各省份的PM10和SO2确实存在空间效应，采用空间滞后模型最合适。（3）汽车尾气排放是NO2的主要来源。随着城市化进程的加快，人们的生活水平不断提高，越来越多的人拥有自己的私人汽车，而随着汽车数量的急剧增加，汽车的尾气排放成为NO2的主要来源，并且其回归模型采用最小二乘估计比较合适。