“均值平方差法”妙解一元二次方程

扬州大学附属中学东部分校初三（5）班 王启昊

我们在列一元二次方程解决问题时，方程的结构类似于两个一次方程的乘积等于某个数值.同学们一般都是整理该方程为一般形式，再运用公式法或者配方法，甚至是因式分解法（十字相乘法）求解.如何巧妙地解这类方程，我发现了一种“均值平方差法”.

我们来看下面这道习题.

（2018·上海静安区二模）今年本市蜜桔大丰收，某水果商销售一种蜜桔，成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克.市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：

（1）求y与x之间的函数表达式.

（2）该经销商想要每天获得150元的销售利润，销售价应定为多少？（销售利润=销售价-成本价）

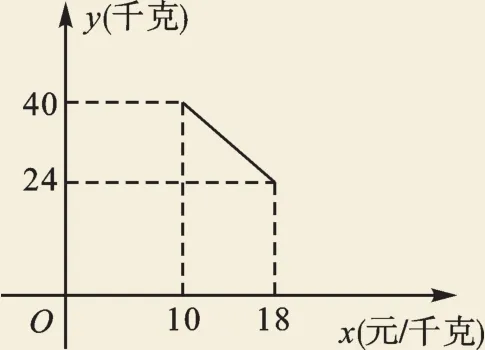
【解析】（1）观察函数图像，找出两点的坐标，再利用待定系数法即可求出y与x之间的函数表达式.

（2）根据“每千克的销售利润×销售数量=总利润”，即可得出关于x的一元二次方程，求解方程并检验.

解：（1）设y与x之间的函数表达式为y=kx+b，把（10，40），（18，24）代入得：

∴y与x之间的函数表达式y=-2x+60（10≤x≤18）；

（2）根据题意，得：（x-10）（-2x+60）=150，整理得：x2-40x+375=0，

解得：x1=15，x2=25（不合题意，舍去）.

答：该经销商想要每天获得150元的销售利润，销售价应定为15元.

请注意，我们在解方程（x-10）（-2x+60）=150时，可以作如下变形：

2.3 模拟“遗传信息翻译”的过程 指导学生阅读教材上相关的文字和图示，理解遗传信息的翻译过程。在进行模拟实验前，思考如下几点： ①如何找出mRNA上的起始密码子、终止密码子？②如何查找mRNA上密码子对应的氨基酸？③核糖体与mRNA的结合部位会形成几个tRNA的结合位点？④是mRNA沿着核糖体移动还是核糖体沿着mRNA移动？⑤二肽和多肽是如何形成的？现在有了模板mRNA、生产厂房——核糖体、原料——20种氨基酸、转运工具——tRNA， 2个学生一组材料，模拟蛋白质的合成。模拟实验步骤如下：

由（x-10）（-2x+60）=150，得：-2（x-10）（x-30）=150，

∴（x-10）（x-30）=-75，那么转化为方程

特别说明：（x-20）是（x-10）与（x-30）的平均数，即这样可以将（x-10）（x-30）转化为含有x的一次多项式与常数的平方差，即为［（x-20）+10］［（x-20）-10］=-75，再转化为（x-20）2=25，然后直接开平方就得到方程的根.这样的解题方法，我命名为“均值平方差法”.老师说，我们将来解决二次函数的实际问题，也可以用这个方法呢！

下面，我们来做另外一道题.

（2018·江苏连云港模拟）无锡市新区某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元/桶，也不得低于7元/桶.调查发现日均销售量p（桶）与销售单价x（元）的函数图像如图所示.

（1）求日均销售量p（桶）与销售单价x（元）的函数表达式；

（2）若该经营部日均获利1350元，那么销售单价是多少？

答：日均销售量p（桶）与销售单价x（元）的函数表达式为p=-50x+850；

（2）根据题意，得：

解得：x1=9，x2=13.

∵销售单价不得高于12元/桶，也不得低于7元/桶，∴x=13不合题意，

答：若该经营部日均获利1350元，那么销售单价是9元.

注意一下：在解方程（x-5）（-50x+850）-250=1350时，方程可化为-50（x-5）（x-17）=-1600，即（x-5）（x-17）=-32，利用“均值平方差法”可得：［（x-11）+6］［（x-11）-6］=-32，

教师点评

数学的学习关键之处是“整体地学，联系地学”，在于提炼与归纳.这篇文章发现了连通乘积式与配方法之间的桥梁，铺设了一元二次方程和二次函数恒等变形的快速通道.