走进中考看“根的判别式”

康海芯

一元二次方程根的判别式是一元二次方程的重要内容，也是各地中考的必考知识.纵观近两年全国各地中考试题中，这部分内容的考查主要包括直接运用根的判别式判定方程根的情况、依据方程根的情况确定字母系数的取值范围等，它通常和其他数学知识结合在一起，注重考查同学们灵活运用根的判别式分析问题和解决问题的能力，试题难度不大，分值占全卷的6%左右.为帮助大家了解根的判别式的有关考点，本文将结合中考题加以分析.

考点1：不解方程判定方程根的情况

例1 （2017·江苏扬州）一元二次方程x2-7x-2=0的实数根的情况是（ ）.

A.有两个不相等的实数根

B.有两个相等的实数根

C.没有实数根

D.不能确定

【分析】先计算判别式的值，然后根据判别式的意义判断方程根的情况.

解：∵Δ=（-7）2-4×（-2）=57＞0，

∴方程有两个不相等的实数根.

故应选：A.

【评注】本题直接考查了一元二次方程根的判别式的知识，解答这类问题的关键是掌握一元二次方程根的判别式（b2-4ac）与一元二次方程根的情况之间的关系.

考点2：根据方程根的情况判定字母系数的取值范围（或值）

例2 （1）（2018·江苏扬州）关于x的方程mx2-2x+3=0有两个不相等的实数根，那么m的取值范围是_______.

【分析】（1）根据方程有两个不相等的实数根可知两个结论：

①该方程是一元二次方程，即m≠0.

②该方程根的判别式大于0，即Δ＞0.

求解上述两个不等式组成的关于m的不等式组即可得到m的取值范围；

（2）根据一元二次方程有两个相等的实数根可得该方程根的判别式等于0，即Δ=0，求解关于m的一元一次方程，然后代入代数式求值即可.

解：（1）∵方程mx2-2x+3=0有两个不相等的实数根，

【评注】一元二次方程一般形式要求二次项系数不为0，这一点在此类问题中经常被忽视；一元二次方程有两个实数根包含两个不相等实数根和两个相等实数根两种情况，也需要综合考虑，不能遗漏.

考点3：判定含有字母系数方程根的情况

例3 （2018·北京）关于x的一元二次方程ax2+bx+1=0.

（1）当b=a+2时，利用根的判别式判断方程根的情况.

（2）若方程有两个相等的实数根，写出一组满足条件的a，b的值，并求此时方程的根.

【分析】（1）先依据根的判别式求出Δ的表达式，利用平方的非负性来判断Δ的符号，然后根据判别式的意义判断方程根的情况.

（2）利用方程有两个相等的实数根得到Δ=b2-4a=0，设b=2，a=1，方程变形为x2+2x+1=0，然后解方程即可.

解：（1）因为ax2+bx+1=0是一元二次方程，所以a≠0，

当b=a+2时，Δ=b2-4a=（a+2）2-4a=a2+4a+4-4a=a2+4，

∴方程有两个不相等的实数根.

（2）∵方程有两个相等的实数根，

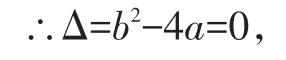
即b2=4a，

因为a，b的取值不唯一，如b=2，a=1，则方程变形为x2+2x+1=0.

解得x1=x2=-1.

【评注】利用根的判别式判定含有字母系数的一元二次方程根的情况时，常用的解法是利用配方法对判别式进行变形，根据平方的非负性证明即可.

考点4：根据一元二次方程方程根的情况确定方程的根

例4 （2018·福建）已知关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（ ）.

A.1一定不是关于x的方程x2+bx+a=0的根

B.0一定不是关于x的方程x2+bx+a=0的根

C.1和-1都是关于x的方程x2+bx+a=0的根

D.1和-1不都是关于x的方程x2+bx+a=0的根

【分析】根据方程有两个相等的实数根可得出Δ=0，即4b2-4（a+1）2=0，得到b=a+1或b=-（a+1）.当b=a+1时，-1是方程x2+bx+a=0的根；当b=-（a+1）时，1是方程x2+bx+a=0的根.再结合a+1≠-（a+1），可得出1和-1不都是关于x的方程x2+bx+a=0的根.

解：∵关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，根据题意得：

∴b=a+1或b=-（a+1）.

当b=a+1时，有a-b+1=0，此时-1是方程x2+bx+a=0的根；

当b=-（a+1）时，有a+b+1=0，此时1是方程x2+bx+a=0的根.

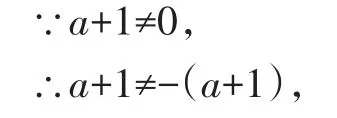
∴1和-1不都是关于x的方程x2+bx+a=0的根.

故应选：D.

【评注】本题考查的是一元二次方程有两个相等实数根的条件下探究根的取值，考查角度新颖.解答这类问题的关键是发现根的判别式与方程之间存在的隐含数量关系.

考点5：根的判别式与其他知识的综合

例5 （2018·湖北鄂州）已知关于x的方程x2-（3k+3）x+2k2+4k+2=0.

（1）求证：无论k为何值时，原方程都有实数根.

（2）若该方程的两实数根x1、x2为一菱形的两条对角线之长，且x1x2+2x1+2x2=36，求k值及该菱形的面积.

【分析】（1）计算根的判别式Δ与0的关系，即可确定原方程根的情况.

（2）根据一元二次方程根与系数的关系及已知条件，可构造关于k的方程，可求得k.菱形的面积等于两条对角线乘积的一半，即

解：（1）Δ=b2-4ac

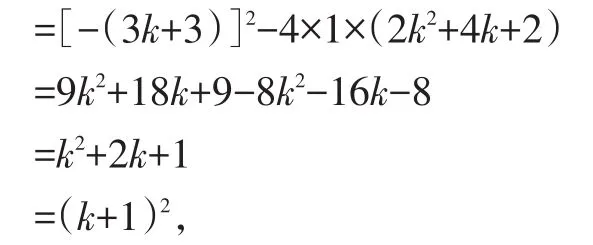
∵无论k为何值时，（k+1）2≥0，

∴无论k为何值时，原方程都有实数根；

（2）由根与系数的关系可得：

【评注】关于x1，x2的对称式通常可以转化成只含x1+x2，x1x2形式的式子，然后将x1+x2=代入.要特别注意一元二次方程根与系数的关系应用的前提条件是方程必须要有两个实数根，即Δ大于或等于0.