掌握技巧，用好“根的判别式”

吴玲芳

在学习了一元一次方程、二元一次方程组、可化为一元一次方程的分式方程后，我们又学习了一元二次方程.不同于之前学习的方程，一元二次方程ax2+bx+c=0（a≠0）的根有三种情况：有两个相等的实数根、有两个不相等的实数根、没有实数根.因为一元二次方程的根与系数之间存在特殊的关系，我们不需要解方程，也能对根的情况做出判别：当b2-4ac＞0时，方程有两个不相等的实数根；当b2-4ac=0时，方程有两个相等的实数根；当b2-4ac＜0时，方程没有实数根.反之，已知方程的根的情况，我们也能得出b2-4ac的正负性.b2-4ac叫做根的判别式，这个式子用“Δ”来表示.用一元二次方程的根的判别式判别方程是否有实根、两个实根是否相等，这是课标的要求，也是中考常考的知识点.如何灵活运用根的判别式？下面为大家提供了一些常见题型的解决方法.

一、方程能解却不必解，利用判别式判断根的情况

解一元二次方程的方法有直接开平方法、配方法、公式法、因式分解法等方法.公式法是配方法的一般化.用配方法解一元二次方程 ax2+bx+c=0（a≠0），配方至时，需要分类讨论.只有等号右边b2-4ac≥0时，两边才能开平方.并且当b2-4ac＞0时，原方程有两个不相等的实数根；当b2-4ac=0时，原方程有两个相等的实数根；当b2-4ac＜0时，由于任何数的平方都大于等于零，此时方程没有实数根.对于给定常系数的一元二次方程，一定可以运用合适的方法求出它的根.但是如果只要了解根的情况，那么仅要算出判别式就能够进行判别.

例1 下列一元二次方程中，没有实数根的是（ ）.

A.x2-2x=0 B.x2+4x-1=0 C.2x2-4x+3=0 D.3x2=5x-2

【解析】本题考查的知识点是根的判别式与一元二次方程的根的关系.

解答：A因为a=1，b=-2，c=0，所以b2-4ac=4-0=4＞0，方程有两个不相等的实数根，故此选项不合题意；B因为a=1，b=4，c=-1，所以b2-4ac=16+4=20＞0，方程有两个不相等的实数根，故此选项不合题意；C因为a=2，b=-4，c=3，所以b2-4ac=16-4×2×3＜0，方程没有实数根，故此选项符合题意；D首先应化为一般形式，得到3x2-5x+2=0，所以a=3，b=-5，c=2，b2-4ac=25-4×3×2=25-24=1＞0，方程有两个不相等的实数根，故此选项不合题意.

故选：C.

【点评】此题主要考查了根的判别式与一元二次方程的根的关系，关键是要准确确定a、b、c.如果方程不是一般形式，要先将方程化为一般形式，再确定a、b、c并代入判别式，计算出判别式的值，最后根据判别式的值再选.因为题目要求是没有实数根，则判别式的值小于0即可.

二、方程不易求解，利用判别式判断或证明根的情况

当一元二次方程的系数中含有字母，一般情况下较难求出方程的根.这类方程的根的情况并不会都随着所含字母的取值的变化而变化，有时因为特殊的数量关系，我们也能利用根的判别式，再结合整式的运算法则、凑平方等方法，判断出根的情况.

例2 下列对一元二次方程x2+（2m+3）x+m2+3m=0根的情况的判断，正确的是（ ）.

A.有两个不相等实数根

B.有两个相等实数根

C.没有实数根

D.无法判断

【解析】本题考查了根的判别式与一元二次方程的根的关系，以及整式的运算法则.

解答：Δ=（2m+3）2-4×1×（m2+3m）=9.

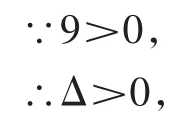
∴无论实数m取何值，方程总有两个不相等的实数根.

故选：A.

【点评】因为方程的系数中含有字母，所以不要再将判别式b2-4ac写出来，直接将各个系数代入Δ，适当地化简就能发现最后的结果与字母m无关，Δ=9＞0，便知道方程有两个不相等的实数根.

例3已知关于x的一元二次方程x2-（m+3）x+m=0.求证：无论实数m取何值，方程总有两个不相等的实数根.

【解析】本题考查一元二次方程的根的情况与根的判别式的关系，以及如何将一个二次三项式通过凑平方，转化成含有完全平方式的式子.

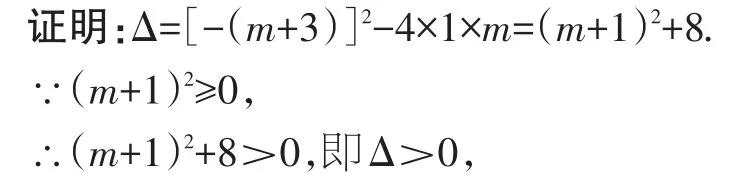
∴无论实数m取何值，方程总有两个不相等的实数根.

【点评】审题时结合条件和结论综合考虑.本题既然要证明有两个不等的实数根，那么通常是利用根的判别式来求解.只有判别式大于0，方程才有两个不相等的实数根.所以首先要写出根的判别式，化简后发现Δ是关于m的二次三项式，可以通过凑平方将它转化，得到Δ=（m+1）2+8，这样的含有m的式子的平方再加上一个常数的式子是大于0的，从而能够完成证明.

三、已知方程的根的情况，利用判别式求字母的值或取值范围

方程的系数中含有字母，已知方程的根的情况，可以根据对应的判别式的情况，利用方程或不等式求出其中字母的取值或取值范围.但是在这类问题中，由于一元二次方程的二次项系数不为0，当二次项系数含有字母时需要注意.审题时，应厘清已知条件中的方程是有解还是无解，当方程有实数根时，应考虑能否是一元一次方程.在一元二次方程的条件下，必须看清是“两个根”还是“两个相等的实数根”，抑或是“两个不等的实数根”.

例4 关于x的一元二次方程x2+4x+k=0有两个实数根，则k的取值范围是（ ）.

A.k≤-4 B.k＜-4 C.k≤4 D.k＜4

【解析】本题考查了一元二次方程根的情况与根的判别式的关系，以及解一元一次不等式的方法.

解答：根据题意得根的判别式42-4k≥0，解一元一次不等式得k≤4.

故选：C.

【点评】本题中一元二次方程ax2+bx+c=0（a≠0）的系数中出现了字母，不要直接用b2-4ac表示判别式，而要将对应的系数直接代入判别式，避免混淆.根据判别式的意义得Δ=42-4k≥0，然后解不等式即可.

例5 关于x的一元二次方程（k+1）x2-2x+1=0有两个实数根，则k的取值范围是（ ）.

A.k≥0 B.k≤0

C.k＜0且k≠-1 D.k≤0且k≠-1

【解析】本题考查了一元二次方程的定义、根的判别式与一元二次方程的根的关系，以及解一元一次不等式的方法.

解答：由题意得k+1≠0且Δ=（-2）2-4（k+1）≥0，即k≤0且k≠-1.

故选：D.

【点评】根据一元二次方程的定义，可知一元二次方程的二次项系数不为0，则有k+1≠0.有两个实数根包括不等和相等两种情况，所以Δ=（-2）2-4（k+1）≥0.然后求出两个不等式的公共部分即可.

变式1关于x的方程（k+1）x2-4x+1=0有两个相等的实数根，则k的取值_______.

【解析】本题考查了一元二次方程的定义、根的判别式与一元二次方程的根的关系，以及解一元一次方程的方法.

解答：根据题意，得根的判别式为42-4（k+1）=0，解一元一次方程得k=3.因为k=3，所以k+1≠0，符合一元二次方程的定义.

【点评】因为方程有两个相等的实数根，所以该方程一定是一元二次方程，所以解题方法类似例5，但是我们审题时一定要看清要求，是“有两个根”还是“有两个相等的实数根”，这样，对于判别式的范围才能用对不等号，才能求出字母的值.

变式2关于x的方程（k+1）x2-2x+1=0有实数根，则k的取值_______.

【解析】本题考查了方程的定义、一元二次方程的定义、根的判别式、解一元一次不等式的方法以及分类讨论的思想方法.

解答：根据题意，该方程可能是一元一次方程，也可能是一元二次方程.

若该方程为一元二次方程，则：k+1≠0且Δ=（-2）2-4（k+1）≥0，k≤0且k≠-1.

若该方程为一元一次方程，则：k+1=0且方程有解.即k=-1.

综上所述，k≤0.

【点评】由于题中已知方程有实数根，二次项系数中含有字母，所以不能确定该方程是一元一次方程还是一元二次方程，因此先分情况讨论，再综合分析.二次项系数指的是一般形式下的情况，如果方程不是一般形式，必须将其转化为一般形式，观察x2的系数，使其不为0，从而解决问题.