电影中概率论和统计学知识的探究＊

张闻锐，万安华



电影中概率论和统计学知识的探究＊

张闻锐，万安华

（中山大学数学学院，广东 广州 510275）

如今，含有数学元素的电影也日益增多，人们在观看这些电影时是否留意并思考过其中的数学问题正是我们所关注的。事实上，这些数学知识对影片的剧情发展往往起到了推波助澜的作用，也为影片增添了独特的魅力与趣味性。选取《决胜21点》和《点球成金》这两部与数学和统计学密切相关的电影，结合具体电影场景研究了其中的概率论和统计学问题，讨论了数据背后的价值和启示。

数学影视；概率论；统计学；大数据

1 概述

电影作为一门流行的现代艺术正受到越来越多人的欢迎，原因不仅仅在于它能带来丰富的视觉与听觉享受，还在于它能用其独有的艺术表现力传播不同领域的知识和文化。如今，含有数学元素的电影也日益增多，人们在观看这些电影时是否留意并思考过其中的数学问题正是我们所关注的。事实上，这些数学知识对影片的剧情发展往往起到了推波助澜的作用，也为影片增添了独特的魅力与趣味性。本文以最近几年的美国电影《决胜21点》和《点球成金》为例，从数学专业知识的角度出发，解释说明影片中出现的概率论与统计学问题，发掘其中所蕴含的数学思想与数学文化。

2 电影《决胜21点》中高低算牌法的探究

2.1 电影《决胜21点》与高低算牌法介绍

电影《决胜21点》讲述了一名教授带领由几名麻省理工的数学高材生组成的团队，利用算牌技巧、暗语和肢体语言，在拉斯维加斯赌场屡有斩获的故事。影片的高亮部分“高低算牌法”体现了概率的奥秘，也体现了几位数学精英对于数学的尖端认识及运算能力。下面我们就电影中的“高低算牌法”以及主角团队作战策略展开详细的讨论。

高低算牌法的原理在于：在实际的游戏过程中，剩余牌的点数大小必定由发掉的牌的点数大小所决定，因而玩家可以计算发掉牌的点数来获知留在牌堆里的牌的点数，从而制定对应的策略。2～6点的牌算作+1，称为小牌；7～9的牌算作0，称为中牌；10、J、Q、K牌（为便于说明下文会写作T牌）和A牌算作－1，称为大牌，将出现过的牌的数值相加。如果数值为正，表明发掉的小牌比大牌多，且数值越大，后面出现大牌的概率就越大；如果数值为负，表明发掉的大牌比小牌多，且数值越小，后面出现小牌的概率就越大。

2.2 关于高低算牌法的概率变化

庄家的固定策略是所有牌点数和小于17点继续拿牌，大于等于17点则停牌。如果玩家此时采取与庄家一样的固定策略，那么当玩家已有牌点数较大时，选择继续拿牌，拿到T牌的概率增大，拿到小牌的概率减小，就会有更加大的爆牌风险。而赌场中21点的规则之一是，如果玩家先爆牌，无论庄家后面是否爆牌，都算玩家输，因此玩家在使用高低算牌法算得牌点数值为正时，应采取另一种策略，避免先发生爆牌而输掉游戏。

2.3 团队作战策略

影片中提到，主角所在团队的作战策略为：团队内分为两类玩家，蹲点员和大赢家。蹲点员负责在各张游戏桌上下最低的赌注，且一成不变，从不加注或者累积下注，在游戏过程中暗自用高低算牌法数点数，等待其桌上的牌“变热”后发信号给大赢家，大赢家此时加入游戏。下面我们将进一步分析这种团队作战策略是基于怎样的逻辑来制定的。

在21点赌场游戏中，玩家一般可以通过2种途径获胜：①玩家所有牌的点数和大于庄家且不超过21点；②玩家未爆牌的情况下庄家爆牌。如果用高低算牌法算得点数为正，那么此时对于玩家来说，无论从上述的哪一种途径，都有较高概率获胜，因为按照团队策略，大赢家在点数为正时加入牌局，拿到大牌的可能性相对较大，有利于大赢家初始牌点数就达到20点或直接拿到黑杰克。另一种可能性则是玩家按兵不动，待庄家选择继续拿牌，拿到大牌的概率也会比较大，从而爆牌的可能性也变大了，玩家也能获胜。当然，概率对于玩家和庄家都是平等的，这意味着庄家初始牌拿到20点或是黑杰克的可能性也变大了，但在实际赌场游戏中，还要考虑玩家和庄家赌注赔率的问题，为了贴近电影剧情以及避免问题复杂化，我们在这里仅仅考虑游戏的胜率，暂时不考虑赔率，所以在出现大牌概率较高的情况下，玩家有更高概率获胜或者至少和庄家平局。由于庄家在牌点数和小于17时会继续拿牌，玩家等待庄家爆牌来赢得游戏的机会可能会更多。总的来说，算牌点数为正时有利于玩家，电影里的主角团队正是利用这个逻辑来提高获胜概率的。

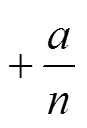
3 电影《点球成金》中棒球统计学的探究

3.1 电影《点球成金》与棒球统计学介绍

电影《点球成金》讲述了奥克兰运动家棒球队总经理比利在耶鲁经济学高材生彼得的帮助下，通过对棒球数据的分析挖掘了一批能力被大众低估的棒球运动员，打破传统的球队经营模式，并带领运动家棒球队取得连胜的故事。面对大量平淡无奇的棒球数据，包括球员打击率、上垒率、盗垒率等，比利和彼得却发现了这些数据背后的信息和价值，建立了精细的数学模型，把上垒率作为挑选球员最重要的指标。这些对以往组建球队的思维方式的颠覆，都是基于棒球统计学而完成的。棒球统计学（Sabermetrics），又称赛伯计量学，是为了评估和比较球员的表现，对棒球数据记录的数学和统计分析。棒球数据主要分为3种：进攻数据、投球数据和防守数据。《点球成金》主要围绕进攻数据展开，即重点衡量一名球员打击和跑垒的表现，因此本文也将主要围绕进攻数据进行讨论。

3.2 上垒率在棒球比赛中的重要性

电影中彼得指出，经营球队的人想的都是怎么买球员，但他们的目标不应该是买球员，而应该是买胜场数，要买胜场数就必须买得分。因而球队获胜的关键是得分，于是比利在面临奥克兰运动家队的三名关键球员被挖走的难题时，采用了以球队整体概念来进行填补的方法，而不是单单找差不多的人去顶替他们。在比利和彼得看来，上垒率这一指标和球队得分密切相关，上垒率越高，意味着出局的概率越低，得分的概率越高，所以他们在挑选球员时注重的也是球员上垒的能力。

为了更清晰、有效地看出上垒率与得分的关系，我们搜集了近50年（1968—2017年）以来美国职业棒球大联盟球队的棒球统计数据，并用R语言对数据进行处理和分析，将上垒率与其他统计量相比较，同时以决定系数作为一个判定基准，来探讨上垒率的意义及其重要性。首先将上垒率作为自变量，球队得分作为因变量，尝试做线性回归，见图1.为了更好地描述变量之间相关的密切程度，我们引入决定系数2作为一个判定基准，其表示的是因变量得分有多少百分比的变异可由自变量上垒率来解释。

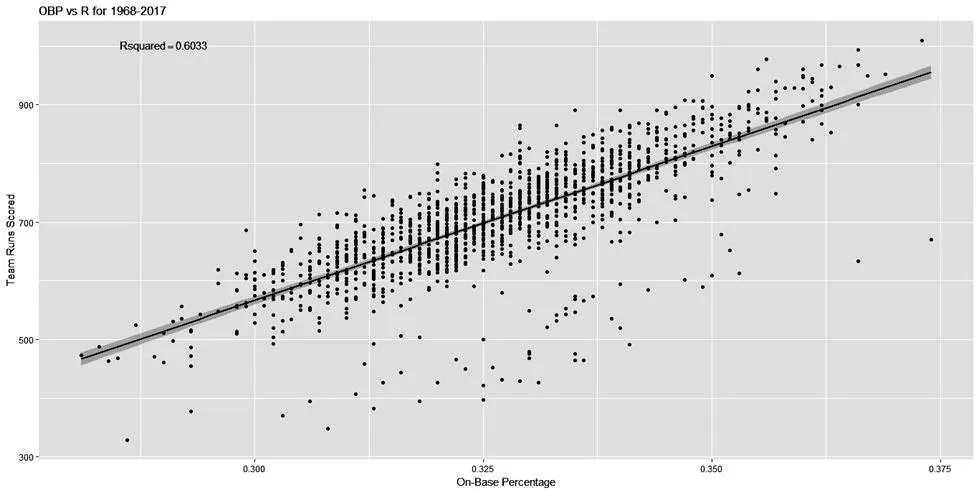
图1 上垒率与球队得分关系图

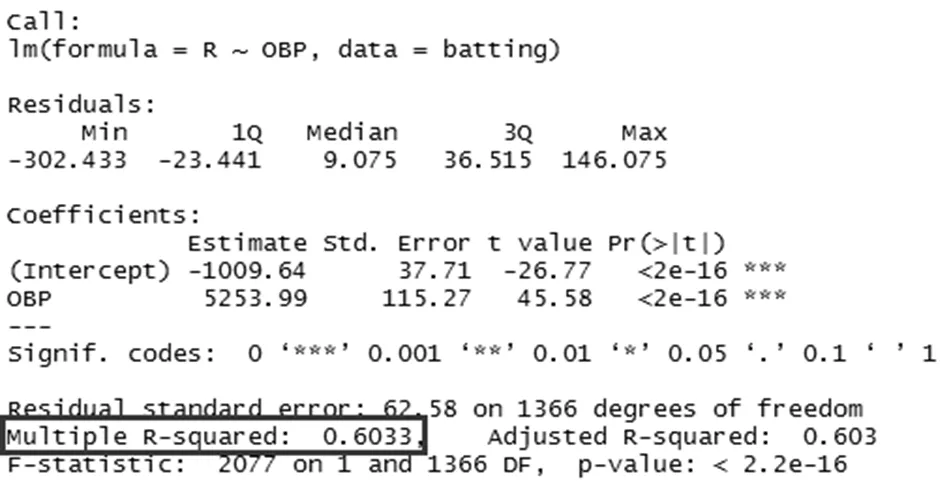
图2 上垒率与球队得分线性回归概述

通过分析数据我们得知，60.33%的球队得分可由上垒率解释，见图2.这个数值较为可观，但我们不清楚它是怎样一个水平，于是我们尝试将上垒率与其他可能与得分呈正相关的变量进行比较，比如打击率和全垒打数，得到二者对球队得分的解释程度分别为49.59%和56.62%.由此看来，上垒率对球队得分的解释程度高于打击率和全垒打数对球队得分的解释程度，是一个比较有价值的指标。

比利在挑选球员时将上垒率作为重要的数据正好就是利用了上垒率与球队得分的关系。运动家队被挖走的球员上垒率分别为0.477、0.324和0.291，平均值为0.364，比利的策略是找到三名球员，他们上垒率的平均值也达到0.364，这样就可以从整体上填补球队上垒率的空缺，整个球队上垒率损失不大，依然有能力得分。

棒球统计学的成功首先在体育界掀起了一场“大数据革命”，它改变了人们对于运动的思考方式，摆脱了对运动员的固有印象，用数据分析的结果去反映事实。在这个大数据时代，大数据已渗透至我们学习、工作和生活的方方面面，数据思维和统计思想变得尤为重要，对于某个社会现象或问题，相关数据的搜集、处理和分析都变得必不可少，人们也逐渐依赖数据去解释问题、监控活动和预测未来。

4 电影背后关于数据的思考

通过对两部电影中数学问题的讨论，我们发现数据背后的确隐藏着具有巨大价值的信息。然而，数据真的可以决定一切事情的走向吗？

《点球成金》中奥克兰运动家棒球队虽然在常规赛中取得连胜佳绩，但在季后赛中却无法晋级。这是因为美国职业棒球大联盟一年的常规赛多达162场，意味着一支球队有足够多的样本量，胜场数就会贴近用棒球数据统计出来的期望值；相反，季后赛采取五战三胜制或是七战四胜制，此时一支球队比赛次数的样本量远远小于常规赛中的162场，而且一旦在季后赛中遭遇淘汰，本赛季中便没有比赛机会使得结果回归预估的期望值，因此季后赛的结果具有较大的随机性，给预测增加了难度。同样，《决胜21点》中主角团队虽然初期“横扫”拉斯维加斯赌场，但后来出现了频频输掉赌局的情况，这里面都蕴含着大数定律和小数定律的奥秘。

由于数据并不代表一切事情的最终走向，在不同的情况下会受到不同因素的制约，因此我们不能过于依赖数据，但我们可以有效利用数据，甚至像两部电影的主人公一样，利用数学去挑战不公平的游戏。虽然影片中的高低算牌法和棒球统计学未能确保最后的成功，但它们都传递了一个非常有价值的理念：我们要敢于利用数据、运用数学与统计学的知识去做出改变，去深入挖掘数据背后隐藏的信息。

5 结论

当严谨复杂的数学与生动活泼的电影碰撞在一起时，不仅能让观众了解数学知识、体会数据之趣，还能呈现出数学在实际生活中的广泛应用，启示人们思考数据的意义、善于分析生活中的种种数据，并利用数学方法去解决实际问题。除了本文所介绍的两部电影之外，还有很多电影也蕴含着丰富的数学元素，其中的相关数学问题都值得去深层次挖掘与探讨。数学与统计学知识在电影中发挥着独特的魅力和价值，使得电影也成为了数学思想与数学文化的一个重要载体。

［1］Ben M.著.季华，季思聪译.迷失的天才［M］.北京：中国青年出版社，2004.

［2］Lewis M.著.郑晓菊译.点球成金［M］.北京：法律出版社，2012.

［3］C.Soto Valero. Predicting Win-Loss Outcomes in MLB Regular Season Games—A Comparative Study Using Data Mining Methods［J］. International Journal of Computer Science in Sport， 2016，15（2）：91-112.

［4］于浩洋，黄亚玲.“大数据”时代体育何去何从［J］.山东体育学院学报，2015，31（2）：5-9.

张闻锐（1996—），女，本科在读，应用统计学专业。万安华（1976—），女，博士后，副教授，主要从事数学教学与科研。

教育部高等学校大学数学教学研究与发展中心教学改革项目（编号：cmc20170404）；中山大学本科教学质量与教学改革工程重点项目（2017）；中山大学国家高等教育质量常态监测数据中心（高等教育研究院）开放基金（A1802）；广东省研究生教育创新计划项目（编号：2017XTLXXM02）

2095－6835（2018）18－0032－04

J904

A

10.15913/j.cnki.kjycx.2018.18.032

〔编辑：辛霞〕