对一种光学中心射线状条纹成因的探究

李文瑶，孙雨彤，周廷明，张君，赵芸赫



对一种光学中心射线状条纹成因的探究

李文瑶1，孙雨彤1，周廷明1，张君1，赵芸赫2

（1.四川省温江中学，四川 成都 611130；2.北京师范大学物理学系，北京 100875）

对使用相机对路灯等光源进行照射时，照片上呈现的放射状条纹现象进行了理论分析、数值模拟和实验验证。理论研究上以正多边形孔的夫琅禾费衍射模型对该现象进行了解释，并采用将正边形分割为个等腰三角形后叠加的方法对正多边形小孔的衍射条纹进行了理论推导，然后利用MATLAB进行数值模拟，模拟结果验证了条纹数与正多边形小孔边数的关系，同时预测了孔的边数、各边长和衍射屏到观察屏的距离对衍射图样的影响。最后通过实验研究定性验证了理论模型的合理性。

放射状条纹；正多边形孔；夫琅禾费衍射；星芒

在晚上使用相机对着街上的灯光拍照，或在阳光强烈的时候透过树叶的缝隙拍摄太阳时，会发现照片上有从光源中心发出的放射状光线。这是摄影中常有的现象，因其现象独特，被称为“星芒”。星芒的尖角数与光圈的叶片数有关——光圈叶片数为奇数时，产生的星芒尖角数为2条；为偶数时，产生的星芒尖角数为条。

通过查阅文献发现对于这种星芒现象的理论解释，仅有一些经验交流称其是因摄像机光圈的衍射现象造成的，没有与实际联系并进行求解。因此，本研究利用正多边形衍射孔的夫琅禾费衍射模型对该现象进行了定性及理论分析，推导并模拟了多边形孔的衍射图像，预测了孔的边数、各边长和衍射屏到观察屏的距离对衍射图样的影响，并利用几何对称性解释了边数与条纹的数学关系，进而通过实验研究将理论模拟结果与实际现象进行对应，定性验证了理论模型的合理性。

1 理论分析

在实际情况中，对比不同相机拍到的同一光源的图片，可以发现不同相机拍出的照片中射线情况并不相同，但是，同一相机拍下的同一张照片中各个光源的射线情况相同。根据以上分析可以发现，照片上的射线并不是光源向外发出的一道道亮光，而是与相机有关的、只存在于照片上的现象。

进一步分析可以发现：①光圈叶片数为奇数时，产生的星芒尖角数为2条；为偶数时，产生的星芒尖角数为条。②光圈越小，星芒尖角越尖锐。③光圈距离被拍摄的光源越远，星芒成像越大、越明显。故推断产生“星芒”现象的主要原因是相机的光圈近似正多边形，如图1所示。光在经过相机的光圈时发生衍射，最后经透镜在CCD（相当于衍射光屏）上呈现出这一现象。

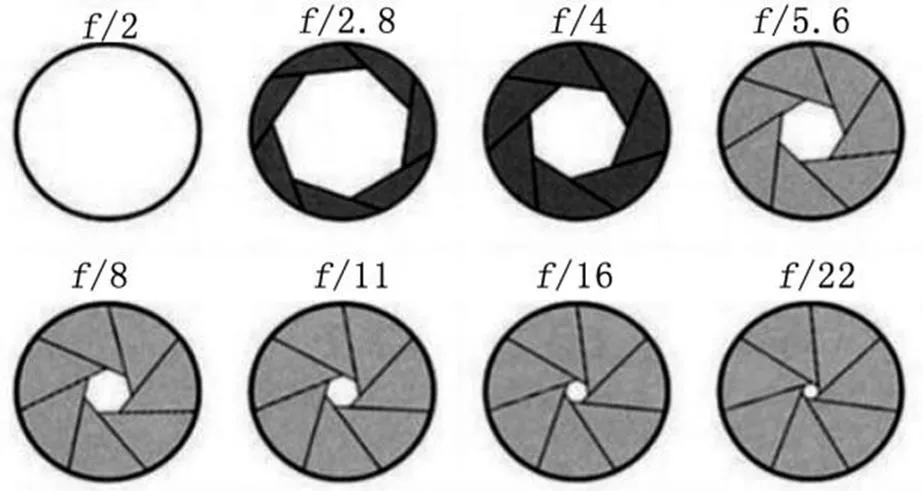
图1 光圈叶片工作示意图

另外，在使用相机拍照时，光圈到光源之间的距离远大于光圈到成像屏上的距离，近似符合夫琅禾费衍射“无限远”的特点，可以看作等效无限远，故本文以正多边形孔的夫琅禾费衍射模型来解释这一现象产生的原因。

对于一个正多边形孔的衍射，直接计算显然并不容易。故采用将正多边形孔分割为多个全等的等腰三角形孔，以其中某一个三角形为基础，对其进行坐标变化后，积分求得整个孔在观察屏上的光强表达式的方式来求解这个问题。

1.1 等腰三角形孔的衍射

首先，考虑最基本的情况，即当发生衍射的小孔是一个顶角为、底边长为的等腰三角形，之后再在此基础上进行变换[1]。

图2 等腰三角形孔的衍射

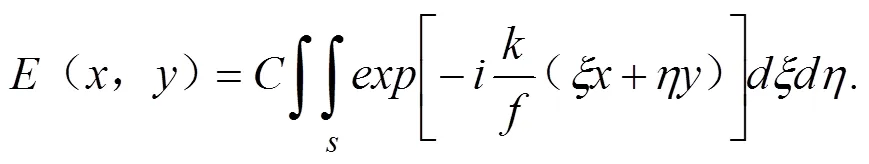
当光的波长确定时，式（1）中的是一个常值（由此也可以看出，如果使用颜色不同的光，成像的规律是不会变化的，只是在分布上呈现定量的规律性差异）。同时，当光的波长确定时，也是一个常值：

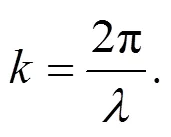
这里表示开孔平面上光的分布（，）它一般是均匀的，在此我们考虑它是均匀的。为方便代入计算，我们令：

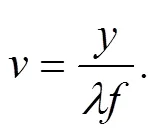
将（4）（5）（6）式代入原式，那么对于此小三角形孔上发生衍射的振幅就可以通过以下积分计算：

（，）就是小孔发生衍射后在观察屏上的振幅分布。

1.2 正多边形孔的衍射

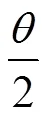
建立直角坐标系，如图3所示，将这个正多边形分解，此正多边形与单个等腰小三角形的面积和角关系就可以表示出来：

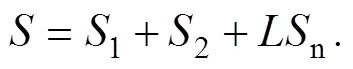
（8）

以等腰三角形1为基础，沿逆时针方向对其进行坐标变化：

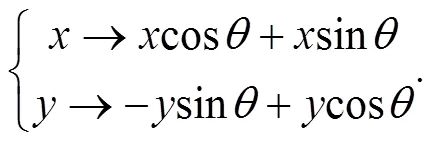
将这一结果用矩阵来表示并进行计算：

对正多边形区域积分可得：

而光强为其复振幅与其共轭复振幅的乘积，故观察屏上的光强表达式为：

另外，可以推断，当→∞时，这个多边形小孔发生衍射将可以近似看作圆孔。

2 数值模拟

将推导出的上述关系编写成代码，使用MATLAB运行程序并绘制观察屏上的光强分布图像（运行环境：MATLAB2016b）。在此，我们考虑3个自变量，即孔的边数、各边长和衍射屏到观察屏的距离，对所涉及的3个变量，控制变量分别对其进行研究，模拟其对成像的影响，得到3组图像（其中，黑色正方形方格的实际大小为1 m2），如图4、图5、图6所示。

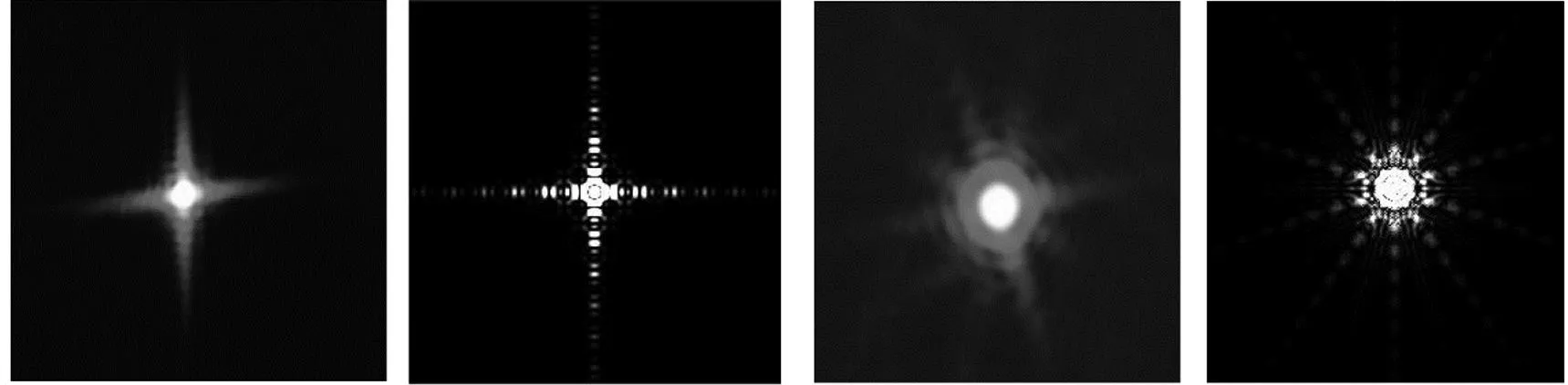
观察这3组图，可以得出结论：①衍射图像呈有共同起点的放射状光束，且中间有一较大的光斑。②条纹以明暗相间的样式延展，且由中心到四周发散，由明到暗并逐渐消失。③当边长与距离一定，边数为奇数时，可观察到2个尖角；边数为偶数时，可观察到个尖角。④当边数与距离一定时，以正六边形为例，随着孔径的变大，呈现的图像越来越小，可观察到的范围越来越大。⑤当边数与距离一定时，随着焦距的变大，视野中可观察到的范围变小，条纹图像越来越大。

图4 a＝3e－5（m），焦距f＝10 m时，改变边数n

图5 当边数n＝6，焦距f＝10 m时，改变孔的边长a（m）

图6 当孔边长a＝3e－5（m），边数n＝6，改变焦距f（m）

3 实验验证

3.1 实验器材及装置

为了验证理论结果，本研究制作了多个不同边数的观察孔片，为了避免“平行光”这一夫琅禾费衍射需要的条件受限，借助激光光学演示仪（型号J-2513）对这些装片进行实验探究。由于手工制作的装片精度不够高，无法精确地控制边长和距离，只能定性地验证上文关于衍射孔边数的结论。

图7为实验环境，图8为实验器材。

图7 实验环境

图8 实验器材

3.2 实验结果

将实验结果与模拟图象进行对比，不难看出实验现象符合星芒条数变化的规律。由于无法精确控制变量，且手工制作和拍摄存在一定误差，结论②和③可以观察到较为清楚的现象。图9为验证实验对比图。由图9可以看到，星芒图样的棱角数与衍射孔边数的关系与理论预言一致。另外，在每一条星芒射线中出现了明暗相见的条纹，这是波动光学现象的典型特征。至此，从实验上说明了星芒的出现是一种波动光学现象，实验结果与理论预测相符。

4 结论

本研究基于正多边形孔的夫琅禾费衍射模型对照相机拍照时出现的“星芒”现象进行了理论与实验研究，得出并解释了星芒条数与光圈叶片数的变化规律，得出了“星芒大小与小孔边长成反相关，与衍射屏到观察屏的距离成正相关”的结论。然后通过自制小孔，对以上结论进行了实验验证，实验现象基本符合理论。

［1］宋易知.任意正多边形小孔夫琅禾费衍射成像探讨［J］.物理实验，2017，37（11）：48-51.

［2］钟锡华.现代光学基础［M］.北京：北京大学出版社，2012.

2095－6835（2018）18－0012－04

O436.1

A

10.15913/j.cnki.kjycx.2018.18.012

李文瑶（2002—），女，四川成都人，四川省温江中学高2017级学生。

赵芸赫（1993—），女，吉林长春人，北京师范大学物理学系2016级硕士研究生，研究方向为物理课程与教学论、IYPT问题解决。

〔编辑：刘晓芳〕