基于泊松碟采样的小生境遗传算法剩余静校正

周 强 曹琳昱 陈爱萍

(①中国石油集团东方地球物理公司物探技术研究中心成都分中心，四川成都 610213； ②中国石油集团东方地球物理公司研究院西南分院，四川成都 610213； ③中国石油集团山地地震技术试验基地，四川成都 610213)

1 引言

山地复杂构造是油气资源的富集区之一。在其形成过程中，经历了多期构造运动，使地表形态和地下构造复杂，静校正问题严重。无论采用折射或层析方法构建的近地表结构，都只是对速度、厚度的一个近似解，不可避免存在剩余静校正问题[1-4]。这将直接影响地震资料成像效果，从而影响对地下构造认识的精度和可信度。

目前主要的反射剩余静校正方法有三种。第一种是高斯赛德尔分解方法，以能量最大确定延迟时，建立反射时间方程组，采用高斯赛德尔迭代求取剩余静校正量，计算速度快。现今主流商业软件大多配备此类模块，该类方法适用于绝大多数地震资料。但由于采用线性方法求解剩余静校正这种典型的非线性问题[5，6]，在处理山地低信噪比资料时，多轮之后会出现剩余静校正量不收敛的现象。第二种是能量迭代法，它对低信噪比资料有一定适应性，但因同一物理点对应的静校正量须满足随机性假设，否则存在累计误差，进而影响计算结果。第三种是非线性方法，包括模拟退火、遗传算法等。常采用不同搜索策略开展全局寻优[7-11]，但存在一个通病就是运算速度极慢，难以满足实际数据处理中的高效要求。因此，亟待研发一种能全局寻优、快速解决山地低信噪比资料剩余静校正问题的、可工业化实施的非线性剩余静校正方法。

本文基于常规遗传算法，利用泊松碟采样生成初始解； 在进化过程中通过多线程构建多种群小生境，采用计算多核并行搜索最优剩余静校正量； 最后应用理论模型和实际资料从效果和效率两方面验证了该方法的有效性。

2 方法技术

Wilson等[12，13]率先将遗传算法应用于求解地震信号剩余静校正量。以叠加能量最大为准则，对多个剩余静校正量组合进行交换、选择、变异操作，最终优选能量最大的静校正量组合，有效地避免了线性方法易陷入局部极值的问题。

常规遗传算法剩余静校正在编代码实现时，因C语言自带的随机函数生成初始种群的随机性不够，采用单一种群容易产生“早熟”现象； 另外，计算效率低也是其明显缺陷。针对常规遗传算法进行剩余静校正存在的弊端，本文设计出一种基于泊松碟采样的小生境遗传算法(图1)，用于更准确地求取地震资料剩余静校正量。

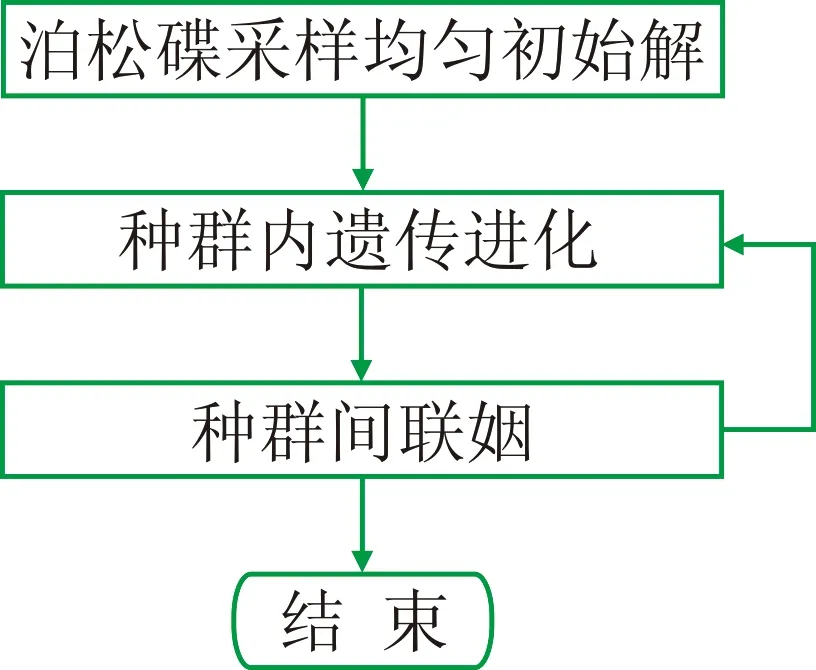
图1 本文方法概要

2.1 泊松碟采样均匀初始解

随机数通常以系统时间为种子生成，随机剩余静校正量基本在同一时间完成，使随机性不够，导致初始解空间不均匀，包含最优解的可能性低，对后期的遗传进化依赖性强，进而影响遗传算法的全局寻优，且搜索耗时长[14]。针对该问题，拟采用泊松碟采样思路。

泊松碟均匀初始解空间的方法是每个剩余静校正量随机生成，任意两个值的差值大于阈值，以该差值为半径的圆内不再生成其他值。具体做法如下。

统计叠前地震数据体中炮点总数(Ns)及检波点总数(Nr)，结合用户设定的静校正量范围[a，b]，并采用实数编码，获取初始解空间

ri,j=U[a,b]

i∈[1,N]j∈[1,Ns+Nr]

(1)

式中：ri，j为初始解，且i为个体序号，j为基因位置；N为一个种群的个体数；U为解空间；a、b分别为最小、最大剩余静校正量。

为了增强初始解遍布解空间的均匀度，采用泊松碟采样方法在全部解空间中抽取相应的个体。具体方法为：首先计算解空间的规模，将解空间的最小范数解与最大范数解之间的距离作为解空间的规模参数

(2)

式中γ、κ分别为解空间中的最小范数和最大范数解。采用下列阈值

(3)

若该阈值不满足，则重复计算；通过筛选迭代，最终获得下列初始种群矩阵

(4)

2.2 种群内遗传进化

种群内采用“精英+赌轮”选择、余下个体与精英两两交叉、小扰动变异策略进行遗传进化，实现全局寻优。

计算种群中每个个体对应的目标函数值，即为种群中个体的适应度值。以剖面能量为例，目标函数计算公式为

]2

si,ns,ri,nr∈R

(5)

式中：Ei为叠加剖面能量；s、r分别为炮点和检波点的剩余静校正量；d为叠前地震信号幅值；nr、ns分别为第i个个体对应的炮点、检波点号；i为个体序号；y为CDP号；h为炮检距；t为时间。根据个体适应度值，保留k个适应度最高的个体作为精英，对余下个体计算选择概率

(6)

式中：E为个体对应的目标函数；P为选择概率；R为个体。之后选择直接进入子代的个体，生成随机数i，若满足

(7)

则选择第i个父代个体进入子代，其余个体依据

r∈U[0,1]

(8)

实现交换策略。若

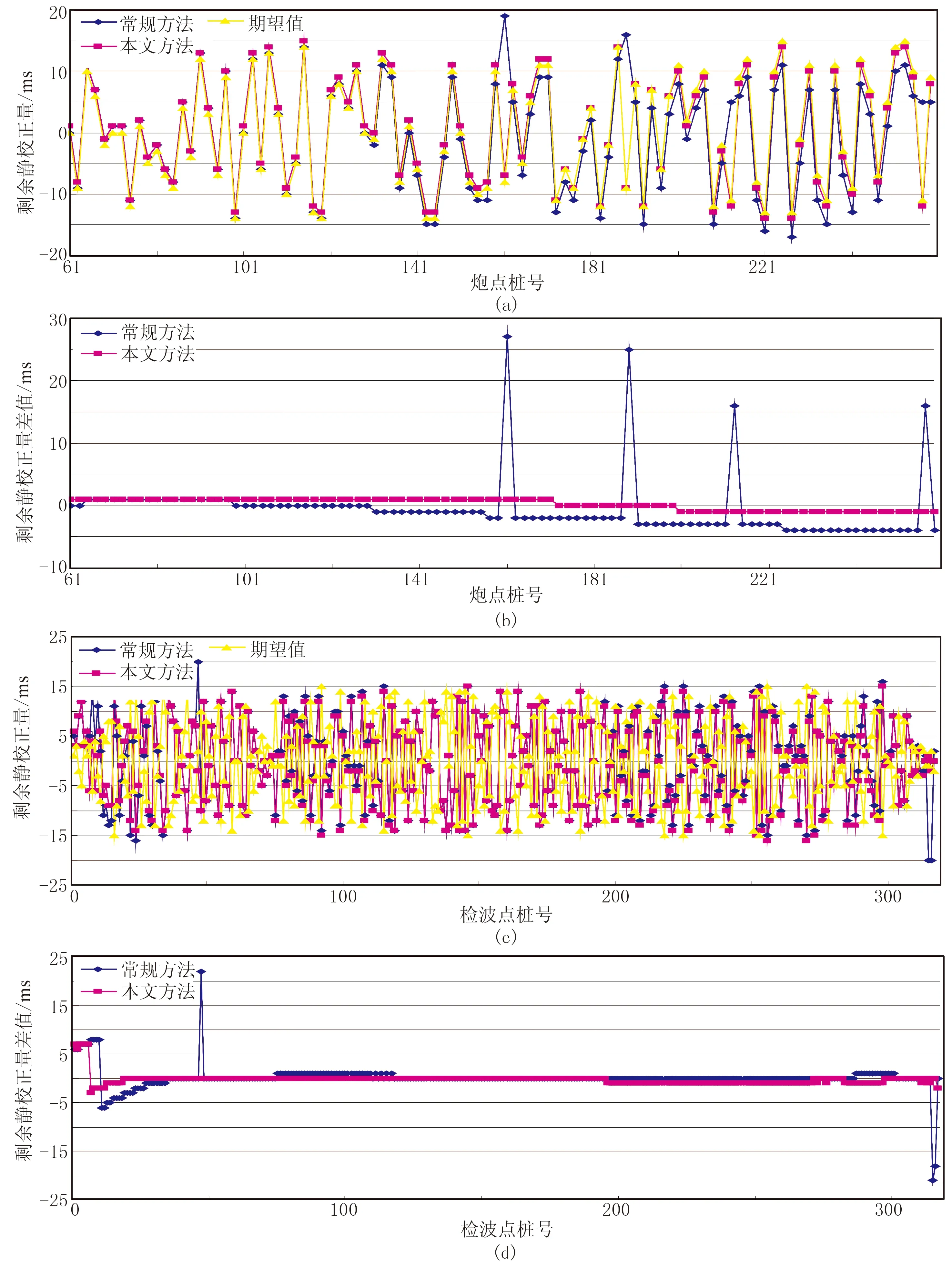
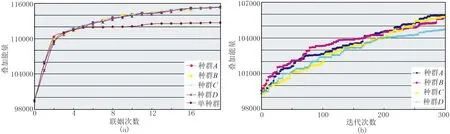
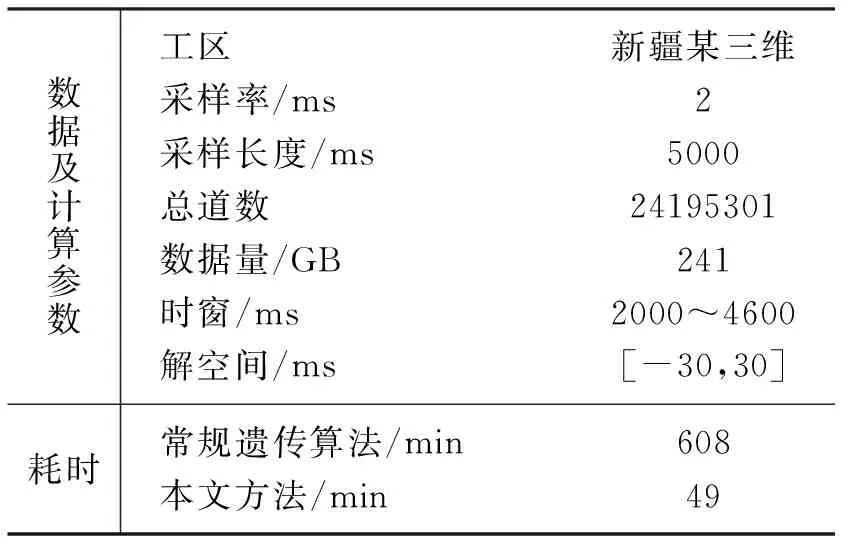
r

(9)

则有

(10)

否则不交换；若交换，即由种群中最优个体与其交换产生新个体。采取两点交换策略，即随机产生两个交换位置，将两个待交换个体中两个交换位置之间的基因段进行交换，产生子代新个体； 否则，父代个体直接进入子代成为子代个体。

对交换后种群，保留k个适应度最高的个体作为精英，其余个体依据变异概率Pm判断是否进行变异，即产生[0，1]间随机数r。若r

(11)

式中：k为常数，可据实际设定；E0为初始目标函数；Eiter为当前代最优解的目标函数； 静校正量范围[a，b]满足

[ri,j-c,ri,j+c]∩[a,b]

(12)

2.3 种群间联姻

常规遗传算法具有极大概率出现早熟现象，即种群中某单个优秀个体的基因会渐渐“统治”其他基因，造成整个种群无法跳出该个体基因的“统治”而陷入局部极值，进而导致算法无法得到最优解。

为了增加基因段的多样性，同时减少早熟现象的发生，采取多种群同时进行遗传操作。如图2所示，在上一轮遗传进化之后，进行联姻操作。具体做法是将每个种群中的适应度函数值最大的个体的大部分基因交换至另一种群适应度函数值中等的个体，再开始下一轮自由进化。该方式下若干不同特征的种群独立进行遗传操作，获得所有种群的一个最优解后，在各种群间进行通婚操作，使得全部种群都可分享优良基因。

图2 多种群小生境遗传算法操作示意图

为进一步提高计算效率，调用omp_set_num_ threads函数设置进程个数。该进程个数取决于设置的小生境种群个数，通常小于CPU的核数，但一般要求不小于4，以确保种群良性发展。每个线程处理一个种群的遗传操作，包括每个个体的基因选择、交换机变异。采用多线程并行方式处理小生境遗传，能充分利用计算机多核更快地寻优。

如此迭代计算，直至达到预设的迭代次数或误差门槛值。几个种群中叠加能量大的个体，即为估算的炮点、检波点剩余静校正量。

3 理论模型测试

构建一个“双平层+单斜层”理论模型。其二维理论数据采用30Hz雷克子波合成，1ms采样，采样长度为1000ms； 观测系统为1785-15-30-15-1785，120道接收，检波点、炮点桩号范围分别是1～318、61～259，满覆盖次数为30。

图3a和图3c分别是炮点、检波点静校正量：黄线为期望值，范围是-20～20ms，有较强随机性； 蓝线是常规剩余静校正量； 粉线是本文方法计算的小生境遗传算法剩余静校正量。三种颜色曲线整体上吻合较好，说明大部分剩余静校正问题已得到解决。但从炮点、检波点静校正量误差值(图3b、图3d)可明显看出，蓝线有个别异常值，说明常规剩余静校正方法存在局部解，而本文提出的小生境遗传算法剩余静校正能全局寻优，未陷入局部解。

从叠加剖面来看，常规剩余静校正的局部解导致剖面上同相轴出现错断及虚假同相轴(图4a)现象，而本文剩余静校正方法除了小号附加段因覆盖参数不足出现稍许弯曲外，其余剖面都恢复了构造形态，且能量得到很好聚焦(图4b)。

进一步分析共中心点道集(CMP1281)。将加入了随机扰动量的道集(图5a)、常规剩余静校正后道集(图5b)与用本文方法的剩余静校正后道集(图5c)进行对比，可见常规剩余静校正的两个局部解造成两道地震道发生了较大时移，在叠加剖面上表现为同相轴的错断。

图6a展示的是小生境遗传算法和常规遗传算法计算的叠加能量(纵轴)随大循环(即小生境算法中的联姻)次数收敛的情况，可见小生境遗传算法最终的叠加能量更大，而常规算法收敛于某一能量值就不再上升，即所谓的“早熟”。

图6b展示的是在第一次循环时，即还没发生联姻前，四个种群各自选择、交叉、变异。其进化过程各不相同，即叠加能量的具体变化不同，而最终的叠加能量是A种群最大，则A 种群中能量最大的精英基因将替代其他三个种群能量处于中间值的个体的部分基因； 之后，四个种群进入下一次大的进化循环。

图3 剩余静校正量及其误差

图4 理论模型成像效果对比

图5 共中心点道集

图6 能量收敛图

4 实际应用及效果

新疆某山地地区断裂发育，地层倾角较大，地下构造复杂；近地表结构复杂，纵横向速度、厚度变化剧烈。无论采用初至折射还是层析折射静校正方法，都只能取得对近地表的近似成像效果，不可避免地存在较严重的剩余静校正问题。

基于此，在进行多轮常规剩余静校正和速度迭代更新后，成像品质仍不能很好地满足地质任务要求。应用本文提出的基于泊松碟采样的小生境遗传算法剩余静校正方法处理后，成像效果(同相轴连续性、波组特征)有了明显改善。

图7a是三维地震M测线经多轮常规剩余静校正和速度迭代更新后的叠加剖面，存在的问题是构造主体部位同相轴连续性不好，地震反射特征杂乱，波组特征不够清晰。应用本文方法后，剖面整体成像效果(图7b)得到改善：同相轴变得连续；尤其是通过细节对比，构造顶部波组特征变得清晰，两翼与顶部的衔接自然连续(图8)。

水平叠加时，剩余静校正和速度更新都需反复迭代，耗费大量时间。而本文方法实现了多线程编程，应用计算机多核优势缩短了估算剩余静校正量的时间。通过效率对比(表1)发现，达到能量增加率终止条件，常规遗传算法需608min，而本文方法只需49min，其处理效率得到大幅度提高。

表1 效率对比表

图7 应用本方法前(a)、后(b)三维地震M测线成像效果对比

图8 应用本文方法前(a)、后(b)叠加剖面构造顶部细节对比

5 结论与讨论

本文提出的估算剩余静校正量的方法，目标函数为反射叠加能量，求解对象为炮点、检波点剩余静校正量； 在此基础上，应用泊松碟采样对求解的静校正量实数编码，增加初始解遍布解空间的均匀度； 构建多种群小生境，种群内采用“精英+赌轮”选择、余下个体与精英两两交叉、小扰动变异策略进行遗传进化，种群间采用多线程同时进化，选出几个种群中适应度最大个体与其他种群联姻，增加基因片段的多样性，避免“早熟”，提高寻优的效率与精度。理论模型和实际数据测试表明，该方法可显著且快速改善剖面成像效果，为复杂地区(尤其是低信噪比)资料提供了一种解决高频静校正问题的实用方法。

本文方法采用了多线程方式，效率提高了约10倍。但随着对地震资料品质要求的提高，高覆盖次数及新老资料的连片处理使得地震数据量急剧增加，要使本文方法具有更强适应性，还需基于地表一致性原则构建MPI框架，以增强超大数据处理能力； 同时应用多节点、多线程对剩余静校正量进行估算，进一步提高计算速度及处理效率。