库车前陆盆地强挤压应力条件下的测井电阻率校正方法

袁 龙 章海宁 李国利 韩 闯 张 文 王 谦

(①中国石油集团测井有限公司测井应用研究院，陕西西安710201； ②中国石油塔里木油田公司勘探开发研究院，新疆库尔勒 841000； ③中国石油西南油气田分公司工程技术研究院，四川广汉 618300)

1 引言

库车前陆盆地地层压力体系复杂，白垩系砂岩储层处于高温高压环境。在强构造挤压应力和重力压实作用下，致密储层呈现特低孔、特低渗特征；同时，受强挤压应力作用，影响地层电阻率测井响应的因素较多，常有水层被误判为“高阻气层”，无法准确有效地识别流体性质[1]。

评价储层的含油性、含油饱和度及划分油水界面的重要指标主要以岩石电阻率为依据[2]。20 世纪初，国外学者开始对岩石电阻率开展大量研究，Brace 等[3,4]分析并研究了在不同恒压和裂隙水压力等条件下发生形变的岩石电阻率变化特征，发现岩石电阻率受饱和度影响很大。Marcela等[5]研究发现未饱和岩石的电阻率随压力和温度升高而呈对数下降，其主要原因是压力的增加改变了岩石孔隙结构特征及其大小，出现压电效应，使导电性能加强、岩石的电阻率下降。这些研究成果均体现岩石电阻率在实验室理想条件下随压力、温度及饱和度等参数的变化规律，不能反映实际地层受多因素影响的岩石电阻率特性。

通过大量室内外承载介质电阻率变化模拟实验研究，取得了许多成果[6-10]，认为：随着施加在岩石上的应力增加，在不同应力阶段岩石电阻率呈现出不同的变化趋势，电阻率曲线先上升，随之保持平稳，然后呈现下降的趋势，并最终在接近岩石主破裂处，电阻率下降至最小值。曲斌等[11]通过模拟不同地层温度与压力条件下不同饱和流体的岩石电阻率的变化规律，发现随地层压力的增加岩石电阻率值呈指数增大。关于岩石电阻率受地应力影响，姜文龙等[12]研究了不同单轴应力条件下砂岩和石灰岩的电阻率在低应力和高应力段的变化情况。郝锦绮等[13]研究认为,在岩石发生破裂前，岩石中存在的裂隙和不同性质的流体是影响岩石电阻率变化的主要因素。这些研究成果主要依靠大量岩心实验数据，但对于实际地层环境下受应力影响的岩石电阻率的变化规律研究较少，对其定量评价研究就更少。

本文基于测井资料、实验数据模拟和理论机理分析，对强挤压应力条件下的电阻率校正方法进行了探索性研究，提出了库车前陆盆地白垩系的电阻率校正方法，最后对比了基于毛管分析J函数求取的饱和度与基于校正后电阻率计算的饱和度，验证了校正电阻率的可行性，形成一套基于地应力的电阻率校正方法。

2 地应力影响下的地层电阻率特征

库车前陆盆地构造带白垩系致密储层的岩性主要为岩屑长石砂岩，平均孔隙度约为5.0%，平均渗透率约为0.05mD，为特低孔、特低渗致密砂岩储层，难以形成优质油气层[14]。诸多学者研究表明[15-20]，库车前陆冲断带受南天山构造挤压应力、上覆盐层诱导及均衡作用，下伏舒善河组巨厚泥岩的拱张作用，形成具有垂向应力差异的背斜三层结构，表现为背斜垂向分层性，形成背斜中和面模式。该模式是在兰姆赛褶皱中和面模式基础上发展而来，表现为在背斜受力变形过程中顶部表现为张应力，底部为压应力，中部则发育一个基本不发生形变的中和面(图1)。

应力中和面决定了白垩系巴什基奇克组储层的分层性。根据划分应力中和面的依据，结合测井曲线、储层宏微观特征、储层类型、裂缝发育情况及应力差变化等综合因素，可划分为垂向三层结构：张性段、过渡段及压扭段(表1)。

张性段：受张应力控制，考虑到山前主要以挤压为主，因此最大和最小应力值较低。主要以孔隙型储层为主，发育张性裂缝，物性最好。纵向上电阻率受裂缝影响，电阻率基线值约15Ω·m。孔隙型储层的原生粒间孔、粒内溶孔、粒间溶孔普遍发育。

过渡段：应力由张应力向压应力过渡，应力值升高，在应力曲线上表现为阶梯式升高。孔隙较为发育，纵向上电阻率差异不大，电阻率基线值约为30Ω·m。储层主要以裂缝孔隙型和孔隙型为主，孔隙度逐渐降低，但局部仍可能呈现较高孔隙度。

压扭段：主要以压应力为主，应力值较高，由于过渡段底部应力接近压扭段应力状态，因此在应力曲线上表现为局部升高，而整体应力值变化幅度不大。微观结构内颗粒受挤压变形强烈、颗粒镶嵌、胶结物挤压变形，鲜见沿缝网的溶蚀作用。

从库车前陆盆地构造带K井区的不同应力类型特征综合表(表1)可看出：随着张性段、过渡段及压扭段依次向下延伸，最大、最小水平主应力值相应增大，地层电阻率值呈现阶梯式增大，其原因是随着地层水平主应力的增大，受主应力差影响，地层孔隙度不断降低，同时伴随着孔隙流体沿着高应力部位向低应力部位渗流，地层电阻率值增大。研究区的构造挤压应力强烈，随最大与最小主应力之差的增大而地层电阻率增大的趋势具有一定规律性。

表1 不同应力类型特征综合表

3 实验及机理分析

3.1 实验

为了更好地研究分析储层条件下的岩心电阻率，利用高温、高压、三轴仪近似模拟储层的温度和压力环境。岩心经过低温干燥、表面清洁及磨光处理、加压饱和盐水后，放入高温高压三轴仪，采用交流二极法、LCR电阻测量仪测量其电阻率(图2)。电阻率计算公式为

(1)

式中：ρ为电阻率；η为测量电阻值；L为岩样长度；S为岩样端面的面积。

3.1.1 实验岩心制备

实验岩样取自库车河露头剖面巴什基奇克组岩性段。其露头储集岩性主要为中粒岩屑砂岩，胶结类型多样，以孔隙式胶结为主，孔隙类型以次生的杂基内溶蚀微孔为主，平均孔喉半径为1.028μm、最大孔喉半径可达75μm，孔隙结构类型以微孔小喉为主，其次为微孔中喉，岩石含有层理结构。

图2 电阻率测量装置示意图

实验岩心的平均孔隙度、渗透率分别为10.04%、3.18mD。首先对岩样按照层理走向进行划分，将岩心加工成5cm×5cm×5cm的立方体。为了保证岩心各项测量参数的精度，使岩心样品X、Y、Z三面的垂直度偏差小于±0.2°，其对应端面的平整度误差小于±0.1mm，边长误差小于±0.3mm。

3.1.2 饱和盐水配置及电阻率测量

由于研究区目的层埋藏深，上覆地层压力大且温度高，地层水矿化度高，配制与地层水相同矿化度的溶液，配用矿化度为180g/L的氯化钠型盐水，15°C时电阻率为0.059Ω·m，密度为1.1314g/cm3。用该溶液对所有岩心进行加压饱和，并对岩心抽真空5h以上，然后加压饱和12h以上，待岩心充分吸水饱和后，加压过程中依然要继续抽真空，以确保岩心饱和100%地层水。

3.1.3 具体步骤

根据研究区构造应力强烈、为走滑型地应力状态(最大主应力>上覆地应力>最小地应力)、存在明显的构造压实作用，该作用受构造应力场和局部构造作用的影响，非均质性非常强，因此设计了对应的物理实验方法。

(1)采用二极法测量方形岩心在受压条件下的电阻率，岩心水平放置在电阻率夹持器内，电极对称布置在岩样的两个端面上，电阻率测量方向始终与轴压方向保持一致，电阻率测量方向及轴压、围压如图3所示。

图3 方形岩心测试方向及轴压、围压示意图

(2)设计轴压(水平最大应力)>围压(上覆地应力、水平最小应力)，在一定温度(90°C)、围压分别为10MPa、20MPa、30MPa、40MPa时，随着轴压递增至70Mpa，分别测量x方向上不同压力下的岩石电阻率值，得到岩石电阻率随水平应力差变化而变化的特征。

3.2 实验结果

不同围压实验条件下，施加轴压前岩石的电阻率值为R0，加压后岩石的电阻率值为Rt。Rt与R0的比值可以明显地表征岩石电阻率值的变化特征，实验得到Rt/R0随水平应力差σ12(最大主应力-最小主应力)变化的曲线见图4。

(2)

式中a、b为区域经验系数，无因次。

图5 不同致密砂岩样品在不同围压下的与σ12的拟合关系

3.3 应力对电阻率的影响机理

Dobrynin[22]和Chierici等[23]研究发现，储层岩石的孔隙度、渗透率、电阻率及密度等物理参数在很大程度上受地层压力的影响。Dobrynin利用描述地层因素与孔隙度φ关系的Archie公式表示电阻率与压力之间的关系

(3)

式中：F0表示地层因数；Rw表示地层水电阻率；m表示胶结指数，无因次。

当施加压力时，假设：①多孔岩石的电阻率变化主要取决于小孔隙喉道的收缩，且小孔隙中主要充满束缚水；②在小孔隙或喉道中存在大量细微颗粒。则式(3)变为

(4)

假设Δm和Δφ都非常小，考虑Δφ趋于无穷小，以至(φ-Δφ)Δm≈φΔm，可得

(5)

(6)

通过大量致密砂岩样品的实验数据分析得到压力函数D(Pp)为

(7)

式中：Pp为地层的孔隙压力；Pm、PM分别为实验最小压力和最大压力。

假设岩石基质压缩系数不变，在一定压力条件下的孔隙度相对变化为

(8)

综合式(6)、式(7)，可得

(9)

式中cPM表示最大孔隙压缩系数，单位为MPa-1。

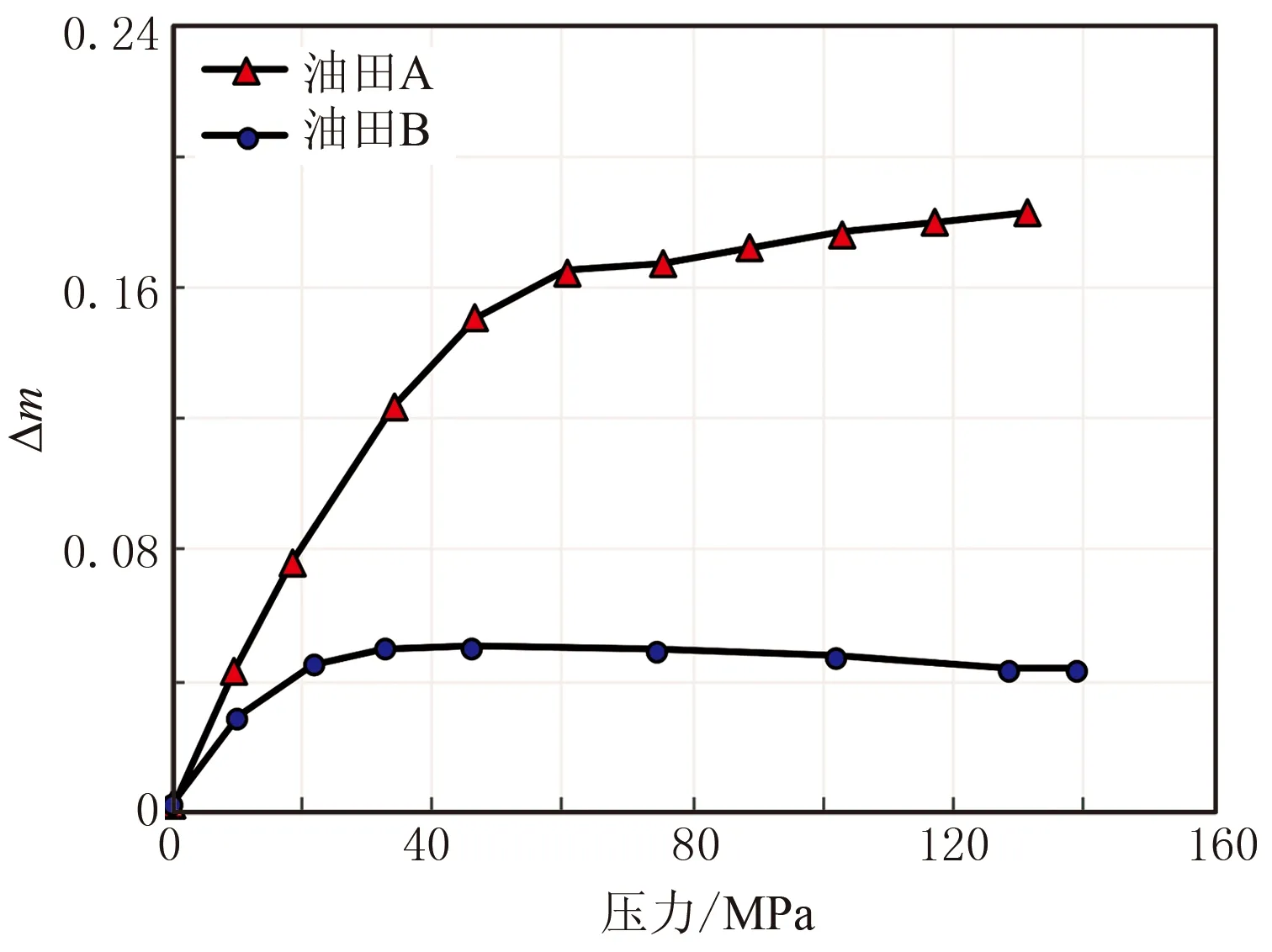
图6 上覆压力对胶结指数的影响

图7 胶结指数对电阻率增大系数的影响

4 电阻率校正方法

4.1 岩石力学参数

考虑库车地区地层异常高压、强应力等实际情况，基于应力分布的几何空间三角函数关系，以地应力实验和压裂实测数据为刻度基准，引用σh-σH模型[24]计算最大主应力σH、最小主应力σh、垂向应力σv， 主要采用密度测井曲线分段求和得到

(10)

式中：H0为无密度测井资料的地层垂直深度；ρ0为未测井段的地层密度平均值；ρi为测井密度值；Di为深度采样间隔，i表示测井曲线的数据点序号；μ为泊松比；α为Biot系数；β1、β2分别为最小和最大水平主应力方向上的构造应力系数，与构造形态有关；Po为上覆岩层压力。

4.2 电阻率校正

通过上面分析得到应力差—电阻率呈指数变化关系，为建立合理的基于地应力校正电阻率的模型提供了可靠的依据。根据实验结果(图4)可知，电阻率比值随水平应力差增加而增大，其变化范围为1～1.4，随着围压增加(10MPa、20MPa、30MPa、40MPa)，电阻率比值相对变小(图5)；再根据实际地层电阻率与水平应力差的相关特征分析，研究区目的层段的水平应力差分别在张性段、过渡段、压扭段不同程度地影响着地层的电阻率(图8)，其中压扭段地层电阻率受水平应力差的影响最大。

图8 地层电阻率与水平应力差交会图

经典Archie实验的电阻率增大率为

式中：Sw为油气层含水饱和度；n为饱和度指数，无因次；b为岩性系数，无因次。对于具有相同岩性、物性和孔隙结构的岩石，含水饱和度的降低是导致电阻率增高的主要因素。结合实际情况分析，对于具有相同岩性、物性、孔隙结构、流体性质及饱和度的岩石，地应力的增大是电阻率增大的主要因素，为此引入一个应力—电阻率增大率参数KI。在张性地层和压性地层中，该参数为水平应力差、有效应力的函数，呈现指数增长的特征，即

(11)

(12)

Pe=σv-Pp

(13)

式中：c、d、e、f为区域经验系数，无因次；Pe为有效应力。

通过分析可知，在张性、压性地层中，当围压、水平应力差均为45MPa时，应力—电阻率增大系数随水平应力差、有效应力的变化特征更符合实际地层情况。

对式(11)和式(12)两边分别取对数可得

(14)

(15)

(16)

将应力—电阻率增大系数的倒数作为校正实测电阻率的系数，并引入工区经验调整系数k(无量纲)，就构成了地应力校正电阻率的模型，即

(17)

式中η′为电阻率校正值。

克深地区巴什基奇克组储集层自上而下可分为张性段、过渡段、压扭段，地层电阻率同时受构造应力、垂直应力挤压，导致地层电阻率增大。相较于有效应力，目的层段的水平应力差对地层电阻率的影响更大，通过该模型进行地应力校正能够得到相对准确的原状地层电阻率。

5 结合压汞资料计算饱和度

5.1 J函数法求取含水饱和度

目前储层含水饱和度主要根据阿尔奇公式或其衍生的公式确定，且主要受电阻率和孔隙度的影响。研究发现，含水饱和度与岩石的微观结构有关，主要是岩石毛管压力函数。由于研究区未进行密闭取心，因此，本文主要采用J函数法并根据岩心资料确定研究区气层段的含水饱和度。

对毛管压力资料经过认真研究和筛选，去掉非储层样品点后，再利用J函数对毛管压力曲线上的毛管压力值(Pc)进行转换，使得各岩样的资料点相对集中，进而反映储层的各项特征[17]。利用J函数对毛管压力数据进行处理，其表达式为

(18)

根据油藏的毛管压力与油水的重力差平衡原理[18]进行计算，即

Pc=0.01(ρw-ρo)H

(19)

研究区束缚水饱和度求取公式为

(20)

将求得的J函数与实验条件下的Swn拟合，得出Swn与J函数的关系式，即

式(18)～式(23)中：σ为界面张力；θ为润湿角；A、B、C、D为区域经验系数；K为渗透率；Swn为标准化后的含水饱和度；Sg为标准化后的含气饱和度；Swi为束缚水饱和度；ρw和ρo分别为水、油的密度；H为自由水面以上的油柱高度。

5.2 效果分析

为了分析基于应力差校正电阻率的效果及适应性，本文选择KS5-1井作为标准参考井。结合地质资料和岩心压汞数据，对KS5-1井巴什基奇克组的第二岩性段进行电阻率校正。通过不同应力类型特征综合表(表1)和KS5-1井应力中和面划分依据对比分析，可以看出KS5-1井6895～6925m段处于过渡段下部，其电阻率曲线较上部电阻率基线有所抬升，因此KS5-1井需要进行电阻率校正。图9为KS5-1井基于应力差校正电阻率后的成果图，最右道为原始含气饱和度值(蓝线)、校正后含气饱和度值(红线)及基于J函数计算的含气饱和度值(黑色柱子)对比图。可见经校正后的饱和度值更加接近于岩心压汞资料分析得到的饱和度值。从图10可以看到，基于校正后电阻率计算的含气饱和度与基于J函数计算的含气饱和度有着较好的相关性，平均相对误差为4.8%，校正前饱和度与基于J函数计算的饱和度评价相对误差为12.9%，说明利用地应力校正电阻率计算模型切实可行。

图9 KS5-1井电阻率校正及岩心饱和度对比图

图10 基于校正前、后测井电阻率计算的饱和度与岩心J函数计算的饱和度交会图

6 结论

库车前陆盆地构造带白垩系目的层的岩性主要为岩屑长石砂岩，为特低孔、特低渗致密砂岩储层。将目的层段的垂向三层结构划分为张性段、过渡段及压扭段，随着地应力增大，地层电阻率值呈阶梯式增大的趋势，且具有一定的普遍规律性。

(1)基于走滑型地应力状态的实际情况设计了近似模拟地层的实验方法进行研究，发现强挤压条件下电阻率比值随水平应力差呈指数型函数增大关系。

(2)研究区储层在张性段、过渡段、压扭段对电阻率的影响呈指数变化规律，因而建立了适合研究区不同应力段的电阻率校正模型。

(3)根据岩心压汞资料，针对不同应力段建立电阻率校正方法，通过典型井的处理分析，认为利用校正后电阻率计算的含气饱和度参数更加准确。