基于Fluent的金属粉末气体输送喷嘴结构设计及优化*

，

(大连理工大学机械工程学院，辽宁大连116024)

裂纹激光修复技术利用大功率激光器对金属件裂纹区域进行加热并在达到基体熔点时填入金属粉末完成缺陷修补。作为一种非接触修复方法，填入粉末的方式方法影响着修复效果[1]。为使送粉系统稳定可靠，形成了以载气式输送原理为基础，由送粉器、喷嘴等构成的多种类型输送系统。喷嘴作为粉末进入熔池前所经过的最后一步，决定着粉末是否能够稳定流出达到预期效果，进一步影响着粉末的使用效率和修复效果，因此送粉喷嘴的设计不可忽略。佟明针对激光快速成形的输送喷嘴，调整粉末通道为两段倾斜结构，减小粉末与边界的碰撞，使粉末汇聚达到要求且利用率较高[2]。杨斌针对激光熔覆场合设计了一体式同轴喷嘴，粉末通道采用光滑倾斜渐缩结构，避免流体流向大角度改变，送粉效果良好[3]。周余针对现有激光熔覆同轴送粉喷嘴送粉和冷却等问题设计了孔式和环式组装型同轴送粉喷嘴，明显增强了送粉稳定性和冷却效果，提高了粉末利用率[4]。Wang W针对气流送粉利用率问题，改用由超声振动提供驱动力的输送装置将粉末送入激光加热区，显著提高粉末的利用率，但是局限于竖直加工工况[5]。综合以上不同场合下送粉系统和喷嘴的设计方法，本文根据小型激光修复设备的要求建立一套送粉系统，设计了适用于该系统的送粉喷嘴，通过调整喷嘴的结构尺寸对气固两相流体进行整流汇聚。

1 微裂纹激光修复送粉系统组成

送粉系统利用气力输送原理，在激光加热过程中同步输送金属粉末。目前将粉末同步送入熔池的常用方法有同轴和侧向两种[6]，通过对比，同轴送粉方法不受加工时轨迹方向约束，有利于粉末准确覆盖裂纹修复区，修复组织具有良好的性能，应用场合更广泛。整个送粉系统主要包括气泵、送粉器、粉末流量检测结构、同轴送粉喷嘴。系统组成及布局见图1。

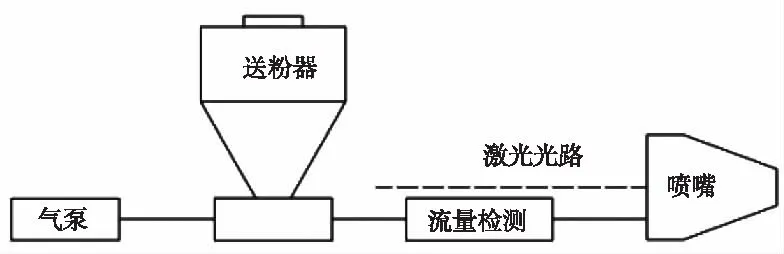
图1 送粉系统

该送粉系统与激光光路同一水平线布置，气体和粉末在送粉器出口处混合，最终通过喷嘴的流体通道输出。为减小管路对流体流动的影响，采用管路走向角度变化小，短距离输送布置方式。这种方式可以有效减小管路对流体流动的影响，但是对于气固两相混合流体，由于金属粉末依托气体流动而流动且金属粉末的跟随性较差，很容易与管路内壁发生碰撞而使流动变的紊乱复杂。这将导致流体从喷嘴输出后金属粉末不会汇聚到一个点上，不仅影响粉末的利用效率而且使修复效果变差。因此，除了考虑流体输送方面的问题，喷嘴结构也决定着能否获得稳定流动的流体。

2 喷嘴结构及设计分析

由于激光经过聚焦系统聚焦，光路形状由平行转为锥形，喷嘴中心腔体采用与光路同轴的圆截面锥形结构，因此取喷嘴粉末出口的间距d1=4 mm，输送粉末颗粒直径较小，取流体出口直径d=1 mm。对于流体的管路输送，常采用较长直管路布置方式，使流体在长直管路流动中逐渐恢复稳定，或者使用某些整流结构。本文送粉系统输送管路较短、占用空间较小且流体由气体与金属粉末混合构成，为使流体输送稳定，采用流体水平直线输送方式，设计喷嘴接口可以与输送管路直接对接；此外，通过修整喷嘴内通道结构，使流体进入喷嘴内部后的流动状态稳定。除了考虑流体的流动稳定性，为实现喷嘴对流体的汇聚功能，喷嘴末端采用锥形结构。综合上述内容及相关文献[7-8]，设计送粉喷嘴剖面及三维结构见图2。

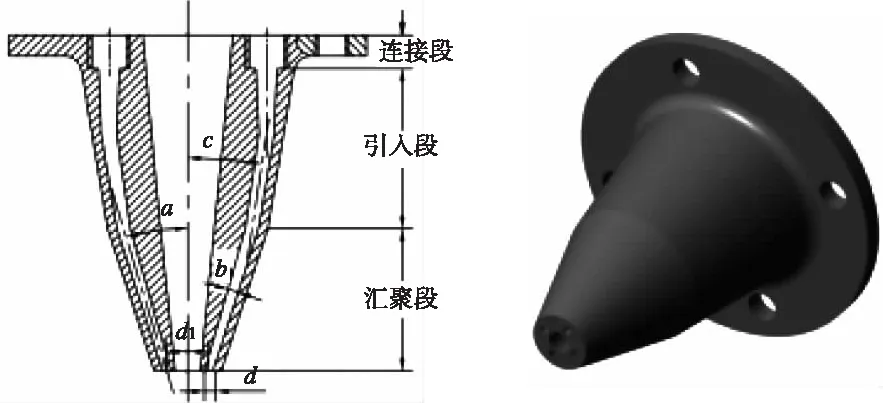
图2 喷嘴结构

整个喷嘴为一体式结构，中间空腔为激光光路通道并以其为中心均布四条流体通道。按流体流动方向将喷嘴划分为两个功能部分，即粉末引入段和粉末汇聚段。引入段包括收缩和倾斜结构，汇聚段为锥形收缩结构。

引入段入口处采用内壁流线型收缩结构，对进入喷嘴的流体进行整流，使流体均匀加速并使气体与固体粉末流线混合收缩，在流出收缩段后流动较均匀，利于流体在后续结构中稳定流动[9]。引入段倾斜部分为等直径倾斜圆柱形管路，连接收缩结构和汇聚段，使用较小的倾斜角度，主要完成流体流向改变。

汇聚段通道采用锥形渐缩方式，实现粉末的汇聚。这部分结构尺寸决定了粉末流体的汇聚效果。

3 仿真方法及假设

为观察流体在喷嘴内部的流动稳定性和汇聚效果，利用Fluent软件模拟该结构中气固两相流体的流动，观察流体流动轨迹和金属粉末流体形成的汇聚焦距和汇聚直径，分析结构尺寸的影响并对喷嘴结构进行修整。

本文中两相流体中金属粉末的体积分数小于10%，将粉末相作离散相处理，采用离散相模型对气固两相流动模拟研究。首先利用standardk-ε湍流模型在流体仅为空气的情况下进行模拟仿真，获得收敛的结构尺寸后，加入离散相模型进行气固两相混合流动模拟，此外需要作出一些理想性的假设[10]：

1)假设两相流在喷嘴入口处混合均匀，稳定流动且具有相同速度，将气体视为不可压缩流体；

2)只考虑流体运动，不考虑传热等问题；

3)假设粉末均为直径0.05 mm的球形颗粒，仅考虑重力，忽略其他力的作用。

4 仿真分析

本文考虑喷嘴对流体流动稳定性和汇聚性的影响。为使喷嘴内的流体具有较好流动特性，喷嘴结构中加入流体引入段，改变流体流向的倾斜角度c值是一个重要因素。

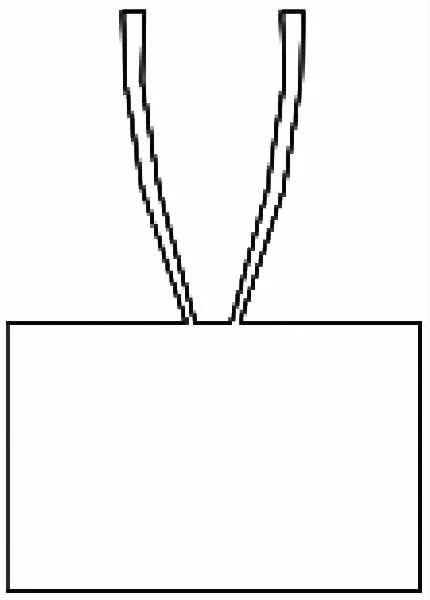
图3 仿真模型

为研究方便，将喷嘴结构简化为仅包含粉末输送管路的二维结构[12]。根据喷嘴结构，在Gambit中建立流场分析模型见图3。将上方入口的边界条件设置为VELOCITY-INLET，根据设计计算取气流速度2 m/s[13]。下方出口边界条件设置为PRESSURE-OUTLET。首先对汇聚段参数a、b进行模拟分析，取得良好的汇聚效果后，在此基础上对引入段的参数c进行模拟设计。

4.1 汇聚性分析

4.1.1 角度a对汇聚性影响

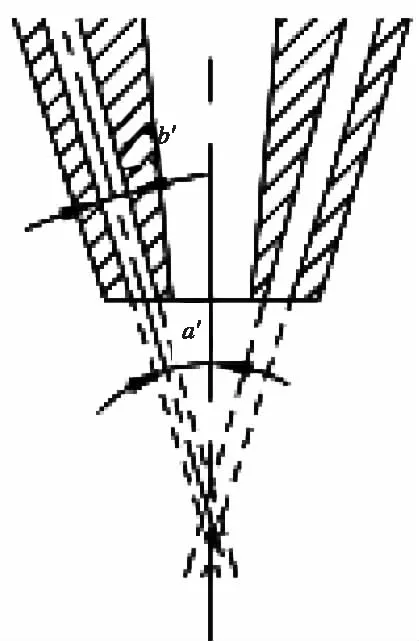
图4 流体理想流动

以理想粉末流体汇聚点为起点经过粉末出口反向进行直线延伸[14]，形成理想的粉末流体汇聚路径，见图4。

以这种情况下锥形收缩通道轴线与喷嘴轴线形成的夹角a′和通道壁面夹角b′为参考依据。根据经验及喷嘴设计要求，取a=15°、17°、19°、21°。通过仿真计算得到数据见表1。

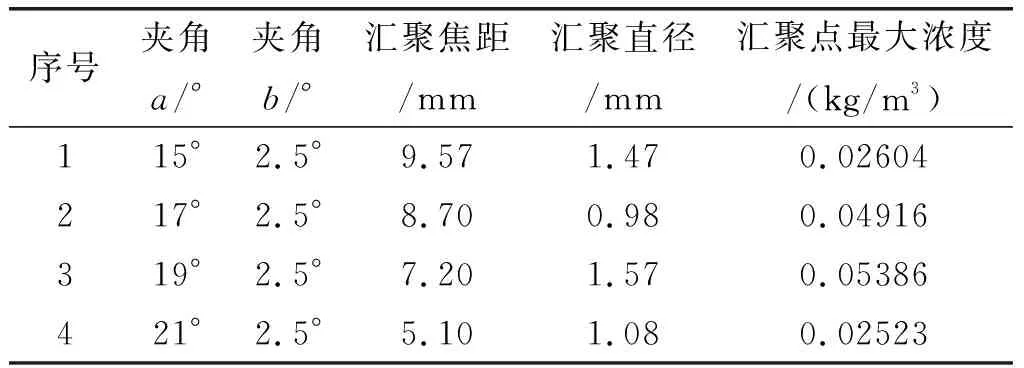
表1夹角a分析结果

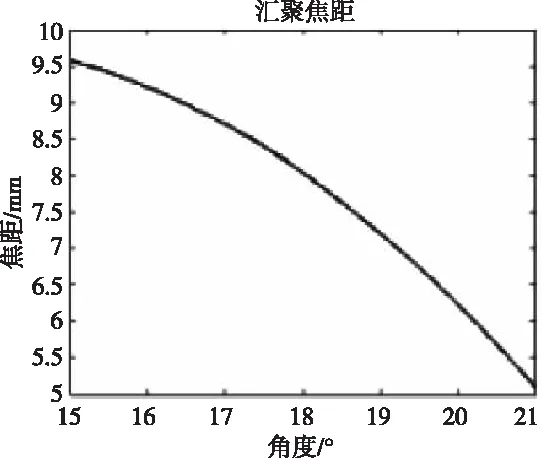
图5 汇聚焦距

根据模拟所得的汇聚焦距值和汇聚点处粉末浓度分布得到如图5和图6所示曲线图。

由以上仿真试验结果图表分析发现，在其他情况确定的条件下，角度a对汇聚焦距影响较大，随着角度a的增大，汇聚焦距数

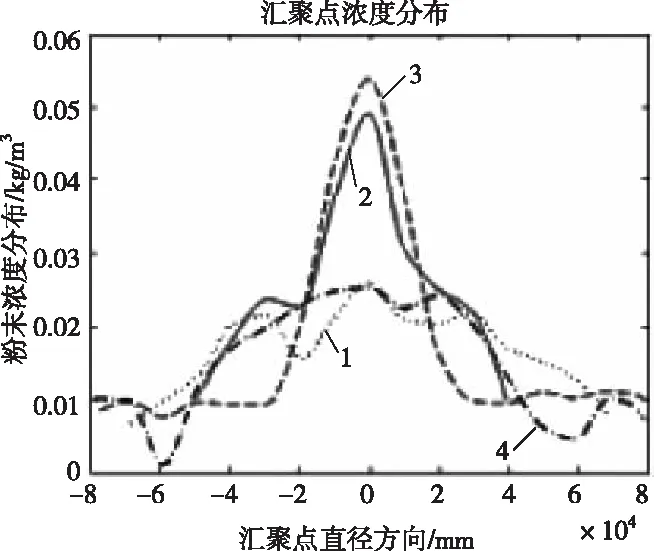
图6 汇聚点粉末浓度分布

值逐渐减小。汇聚点处粉末浓度曲线近似于峰形。第2组的粉末汇聚直径较小，且浓度分布较高，粉末输出更加集中。综合对比分析各组模拟结果的参考数值，当角度a=17°时汇聚焦距、汇聚直径接近设计要求且粉末浓度分布较高，喷嘴具有良好的汇聚效果。

4.1.2 角度b对汇聚性影响

在轴向夹角a=17°的条件下，考虑壁面夹角b的大小对粉末流动效果的影响。取b=2.5°、3°、3.5°、4°，经过模拟分析得到结果如表2。

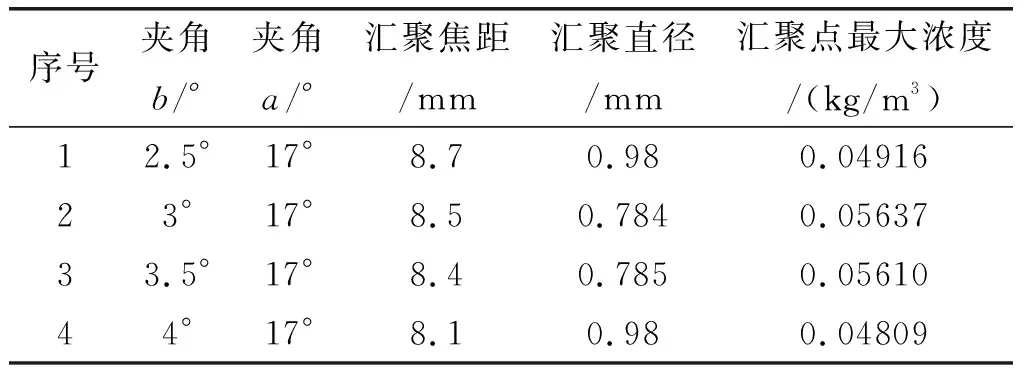
表2夹角b分析结果

汇聚点处直径方向粉末浓度分布如图7。

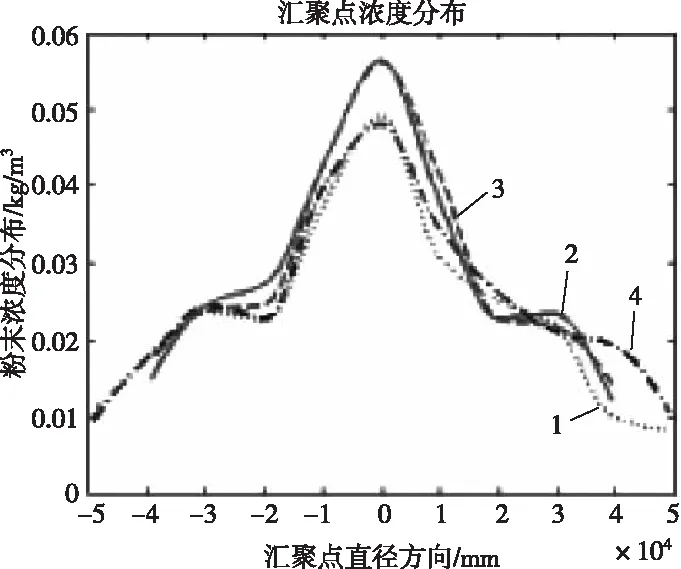
图7 汇聚点粉末浓度分布

由以上图表可以看出，夹角b的变化对粉末汇聚焦距和汇聚直径的影响较小，但是对汇聚点粉末的浓度分布起到一定优化作用。分析图表中三种参考数值，夹角b=3°时汇聚焦点直径和汇聚焦距达到设计要求，粉末输出更加集中，提高了汇聚点处粉末浓度，有利于获得良好修复组织及形貌，且有利于增加粉末的利用效率。

综合以上结果，该喷嘴在轴线间夹角a=17°和通道壁面夹角b=3°的情况下满足设计要求，且具有良好的汇聚性。

4.2 稳定性分析

与未加入喷嘴引入段的普通喷嘴结构相比，对于固体粉末流动，引入段的加入可以减少粉末流体在管路流动中的往复碰撞，流体在经过引入段进入汇聚段的过程中流动更加稳定。因此，在上述所得汇聚段结构参数的基础上，对倾斜角度c的值进行考虑。通过改变倾斜段角度c的值，模拟喷嘴内部流场的流动效果，观察流体流动稳定性，得到结果如图8。

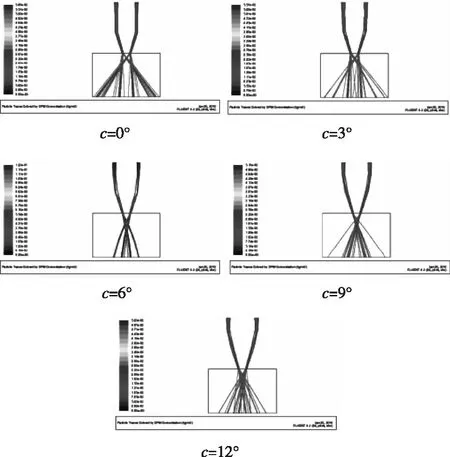
图8 粉末轨迹

当角度c由0°变化到12°，观察喷嘴内部粉末流体的流动轨迹。0°时即不加入引入段的喷嘴结构，该种情况下粉末流体与边界反复碰撞，造成流动紊乱。随着角度c的增加，粉末流体的汇聚性逐渐变好，当角度c继续增加流体又会发生紊乱现象。当c=9°时流体流动稳定，具有较好的汇聚性。

4.3 三维仿真结果

根据以上喷嘴尺寸结构优化结果，选取模拟得到的最佳设计参数，建立喷嘴三维结构分析模型进行仿真计算[15]，使用与上述二维模拟相同的假设条件和模拟方法，观察三维模型中流体流动情况。如图9所示，三维结构内流体流动状态较稳定，汇聚性较好。

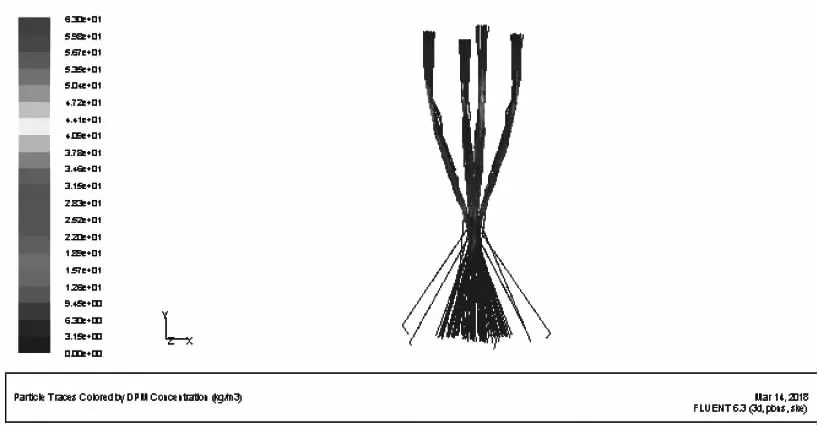
图9 三维结构内粉末流动轨迹

流体汇聚处粉末斑点近似于圆形，如图10所示，当设备随着裂纹路径的变化而任意角度移动时，输出流体可以较好覆盖修复区且铺料均匀，能够获得较好的修复形貌，提高修复质量。

图10 粉末汇聚点形状

5 结论

1)根据粉末输送要求，设计送粉喷嘴结构。将喷嘴划分为引入段和汇聚段，喷嘴引入段使固体粉末流具有良好的流线形状，确保流动的稳定性，喷嘴汇聚段引导流体汇聚，满足设计要求。

2)通过考虑同轴送粉喷嘴的送粉结构，在已知流体通道出口直径和出口间距的条件下，利用Fluent构建离散相模型进行流体运动模拟可知，随着a的增大，汇聚焦距数值逐渐减小，夹角b的值对汇聚点直径和粉末浓度分布存在一定影响。综合考虑固体粉末的汇聚焦距、粉斑直径、浓度分布，当a=17°，b=3°，c=9°时喷嘴达到设计要求，经三维仿真分析，流体的流动效果较好。