基于自组织递归模糊神经网络的PM2.5浓度预测

周杉杉，李文静，乔俊飞

（1. 北京工业大学 信息学部，北京 100124; 2. 计算智能与智能系统北京市重点实验室，北京 100124）

近年来伴随我国多个城市空气重污染事件的发生，以细颗粒物(PM2.5)为特征污染物的区域性大气环境问题逐渐引起了人们的广泛关注[1]。2012年环保部发布了新修订的《环境空气质量标准》(GB3095—2012)，将PM2.5纳入空气质量监测范围。2013年国务院发布了《大气污染防治行动计划》，制定了明确的大气污染防治目标。但截至2016年中国环境状况公报发布的数据，全国338个地级及以上城市只有84个城市空气质量达标，以PM2.5为首要污染物的天数达到80.3%。我国城市空气污染是长期形成的复合型大气污染，治理工作还需要我们长期不懈的努力。

据研究PM2.5可以渗透到人的肺部和支气管，因此长期暴露于PM2.5环境中会增加呼吸系统和心血管疾病的发病率和死亡率[2]。通过对太阳辐射的吸收和散射，PM2.5也会对全球气候变化产生影响，同时会影响能见度，进而影响我们的日常生活[3]。因此，对PM2.5进行有效的预测，及时采取防控措施有重要意义。但是PM2.5的浓度既和污染源有关，又受气象条件的影响，使得预测难度较大。

目前空气质量预测方法主要有机理分析和统计模型两种。机理分析法通过研究PM2.5的形成机理，复杂的物理、化学变化来模拟其扩散过程，进而预测PM2.5的浓度。比如，Saide等[4]利用化学传输模型，根据示踪物CO浓度与PM10/PM2.5的线性关系得到PM10/PM2.5的预测浓度，其中模型所需的排放源清单的准确性对预测结果有显著影响；Riccio等[5]利用欧拉模型和拉格朗日模型对意大利南部某站点的PM2.5浓度变化情况进行了模拟，得出了当地PM2.5的浓度不但受本地排放源的影响，同时与周边区域的输送有关的结论。但是，大气环境是动态变化的非线性过程，理论分析复杂，机理分析建模所需的气象边界条件、排放源清单等参数难以取得，模型的适用性较难满足，不适合日常PM2.5浓度的预测。

相比于机理分析方法，统计模型更容易通过数据拟合方法建立预测模型。Chen等[6]使用小波分解和逐步回归结合的方法来预测PM10的浓度，取得了不错的预测效果；Elbayoumi等[7]以室外 PM10、PM2.5、CO、CO2浓度、风速、气压和相对湿度作为输入，建立多元线性回归模型(multiple linear regression，MLR)预测室内 PM10和PM2.5的浓度。而PM2.5浓度变化是非线性过程，对其建立线性模型效果并不理想。

人工神经网络(artificial neural network，ANN)因其强大的非线性映射能力、自组织自学习能力，被广泛用于非线性系统的建模。Ordieres等[8]利用多层感知器和径向基函数(radial basis function，RBF)神经网络预测PM2.5浓度，发现RBF神经网络预测结果更精确；Xu等[9]利用回声状态网络预测上海市区PM2.5日均浓度，以更少的输入取得了比RBF更好的预测效果，但是预测精度仍需进一步提高。由于神经网络是“黑箱模型”，可解释性差，模糊系统则可以利用模糊语言处理信息，表达能力较强，因此结合两种方法的优势对PM2.5浓度进行预测成为提高预测精度的有效方法；Mishra等[10]以 CO、NO2、O3、SO2、上一时刻的PM2.5浓度、温度、风速、相对湿度和露点温度作为输入，利用Takagi Sugeno型模糊神经网络预测当前时刻的PM2.5浓度，取得了比MLR和ANN更好的效果；Qiao等[11]利用模糊神经网络建立PM2.5小时预测模型，并采用二阶梯度下降算法训练网络，预测效果比ESN和化学传输模型都要好。另外，PM2.5的浓度扩散是一个非线性动态变化的过程，受到时滞的影响。相对于前馈神经网络，递归神经网络具有动态元素，内部的反馈连接可用于记忆历史信息，更适合处理非线性动态过程。因此，本文提出采用递归模糊神经网络(recurrent fuzzy neural network，RFNN)预测PM2.5浓度。

对于神经网络而言，网络结构的大小是影响其性能的重要因素，结构优化方法主要有增长型、修剪型和增长修剪相结合等方法。而很多方法在判断是否增删神经元时需要预先设定阈值，这些阈值的设定通常凭借经验多次试凑，不能保证找到最优值[12-14]。针对以上问题，本文提出一种神经网络结构自组织方法，采用ε准则和偏最小二乘法(partial least squares，PLS)定义增长和删减指标，使用尽量少的阈值，实现规则化层神经元的自动增删，同时采用学习率自适应的梯度下降算法对网络参数进行优化，并将该自组织递归模糊神经网络用于PM2.5浓度预测实验。

1 递归模糊神经网络

RFNN结合了神经网络与模糊系统的优点，引入的递归环节可以增加网络的动态记忆性能。文中RFNN的结构如图1所示。

图 1 递归模糊神经网络结构Fig. 1 Structure of recurrent fuzzy neural network

网络隶属函数层采用高斯函数对输入变量进行模糊化处理，如式(1)所示。在规则层引入反馈环节，通过sigmoid函数将上一时刻规则层的输出作为当前规则层的一个输入，计算过程如式(2)～(4)所示。去模糊化层和输出层如式(5)～(6)所示。式中：uij(t)为t时刻第i个输入对应的第j个隶属函数的输出，cij(t)和σij(t)分别为对应隶属函数的中心和宽度。

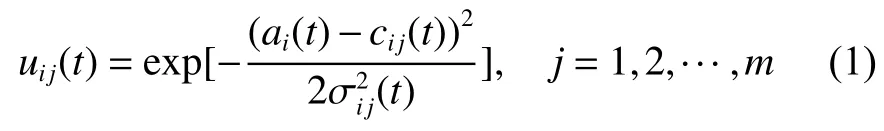
式中：ϕj(t)是t时刻第j个规则层神经元的输出，ϕj(t-1)表示前一时刻规则层的输出，fj是对应的sigmoid函数，hj是内部变量，λj(t)是t时刻递归环节的反馈权值。

式中：y(t)是t时刻神经网络的输出，wj(t)是t时刻输出层与前一层的连接权值，是去模糊化层的输出。

为了提高网络的收敛性，本文采用学习率自适应的梯度下降算法调整递归模糊神经网络的参数。

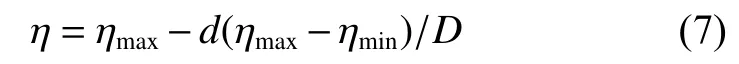
2 自组织递归模糊神经网络

神经网络的结构是影响其性能的关键因素之一，本文根据模糊规则的ε完整性准则和偏最小二乘法实现网络规则层的自组织，结构如图2所示。

图 2 自组织递归模糊网络结构Fig. 2 Structure of self-organizing RFNN

2.1 结构增长

1)定义判断误差e。为了减小异常数据的影响，文中采用滑窗方法：

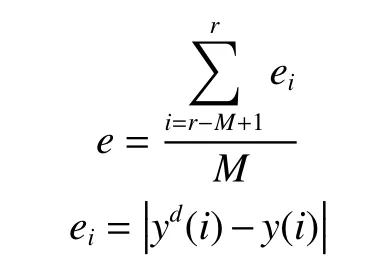
式中：M是滑窗宽度。若误差e变大，则说明网络泛化性能变差，需要增加模糊规则或者修正参数。

因此，如果满足条件：

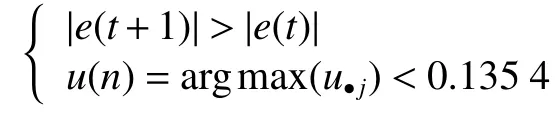
则说明当前网络误差变大，现有规则不能有效覆盖输入数据，需要增加规则层神经元(将规则层第n个神经元分裂为两个)。新增神经元的初始参数设置为

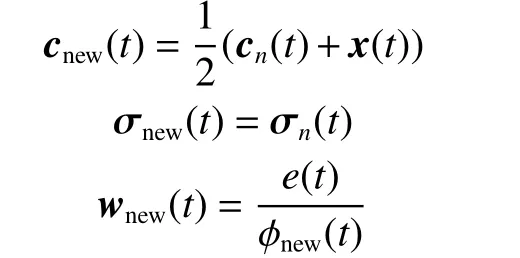
式中：cnew(t)、σnew(t)和wnew(t)分别是新增神经元的中心、宽度和连接权值，cn(t)和σn(t)是第n个神经元的中心和宽度，x(t)是当前输入样本，ϕnew(t)是新增神经元的输出。

2.2 结构修剪

模糊神经网络规则层的删减一般根据规则层神经元对于输出层神经元的影响大小来判断。这种删减也可以理解为一种数据的降维。因此，基于数据降维的思想，本文采用偏最小二乘算法实现规则层神经元的修剪。偏最小二乘算法的一个显著特点就是允许在样本点个数少于变量个数的情况下进行回归分析。由于滑窗宽度有限，可能出现滑窗内样本个数少于规则层神经元个数(即变量个数)的情况，所以采用PLS算法正好解决这一问题。以下是删减过程的主要步骤：

首先判断误差 e，如果|e(t+1)|＜|e(t)|，说明当前网络性能较好。接下来通过PLS计算规则层神经元的回归系数，删除对输出影响较小的神经元以避免网络结构冗余。PLS主要计算步骤如下：

1)以滑窗内规则层神经元输出作为自变量X，网络输出层神经元作为单因变量y。X和y经标准化后的矩阵分别记为E0和F0。

2)从E0和F0分别提取第1个成分t1和u1。提取成分时，t1与u1要尽可能多地携带原数据的信息且相关性最大，从而保证自变量成分t1对因变量成分u1的解释性最强。如果第1个成分不能满足精度要求，则用残差矩阵E1和F1继续提取第2个成分，直至提取的成分个数满足算法的停止要求。

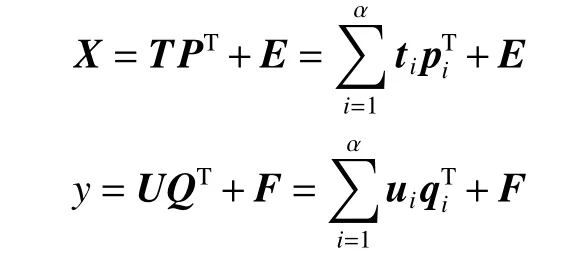
式中：T、P、E分别是自变量X的得分矩阵、负荷矩阵与残差矩阵；U、Q、F分别是因变量y的得分矩阵、负荷矩阵与残差矩阵；α是提取的成分个数。

3)通过检验交叉有效性确定最终提取的成分个数。首先从所有n个样本点中除去第i个样本点(i=1,2,···,n)，用h个成分拟合一个回归方程。将被除去的样本点i代入该回归方程，得到y在样本点i上的拟合值。对i=1,2,···,n重复上述计算，则因变量y的拟合误差平方和为

其次，将所有n个样本点用于拟合含h个成分的回归方程，记第i个样本点的拟合值为，得到y的误差平方和为

定义交叉有效性

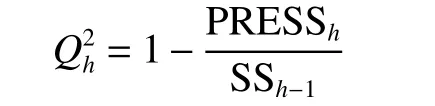
通过计算回归系数Rj，当规则层神经元的最小系数R小于阈值Rth时，则删除该神经元。

若第j个神经元被删除，则与第j个规则层神经元欧氏距离最近的神经元参数调整为

3 实验研究

3.1 非线性系统辨识

为验证SORFNN模型的有效性，采用典型的非线性系统：

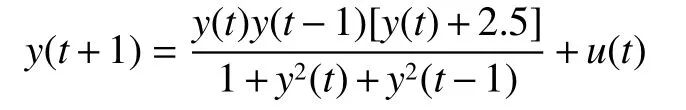
进行实验验证。其中，y(0)=0，y(1)=0，u(t)=sin(2πt/25)。非线性系统的模型为

因此SORFNN模型为3输入1输出，根据式(8)产生500个样本，训练数据采用前400组，后100组用于测试，为了验证神经网络的自组织结构变化，初始规则数选取较小值2。

图3给出了训练过程中规则层神经元个数的变化情况，最终神经元稳定在6个左右，表明网络结构能够动态优化，提高网络性能。图4和图5分别给出了网络训练效果和测试效果。从图中可以看出，网络在训练和测试阶段与期望输出都拟合较好。

图 3 规则层神经元变化Fig. 3 Number variation of neurons in rule layer

图 4 训练效果Fig. 4 Training results

图 5 测试效果Fig. 5 Test results

图6是样本的测试误差图，图7是测试输出与期望输出拟合的散点图。从图中可以看出网络测试误差较小，测试输出与期望输出基本拟合在一条直线上。表1给出了SORFNN与动态模糊神经网络 (dynamic fuzzy neural network，DFNN)[16]、广义动态模糊神经网络(generalized dynamic fuzzy neural network，GDFNN)[17]和基于本文自组织方法的自组织模糊神经网络(self-organizing fuzzy neural network，SOFNN)的性能比较。

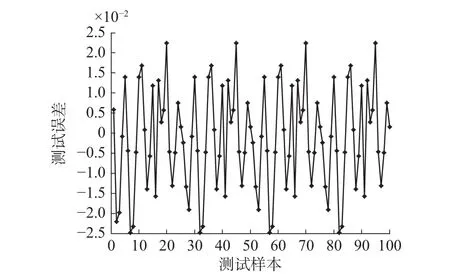
图 6 测试误差Fig. 6 Error of test

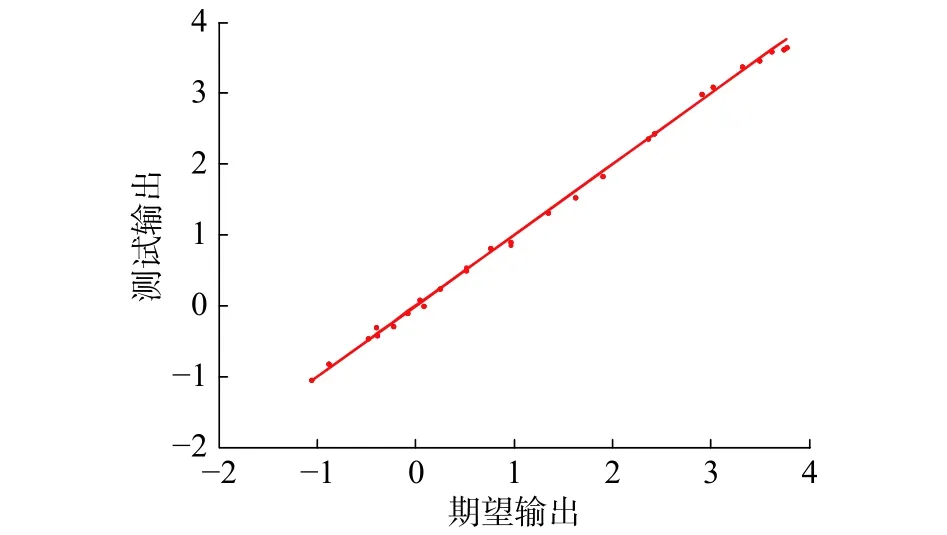
图 7 测试散点图Fig. 7 Scatter plot of test

从表1可以看出，SORFNN的测试RMSE为0.009 1，明显小于其他算法。规则层神经元个数为6，结构较为紧凑。同时，该自组织算法计算时间明显小于其他算法。对比结果表明SORFNN不仅能够获得较为精简的网络结构，而且性能同样可以满足要求。

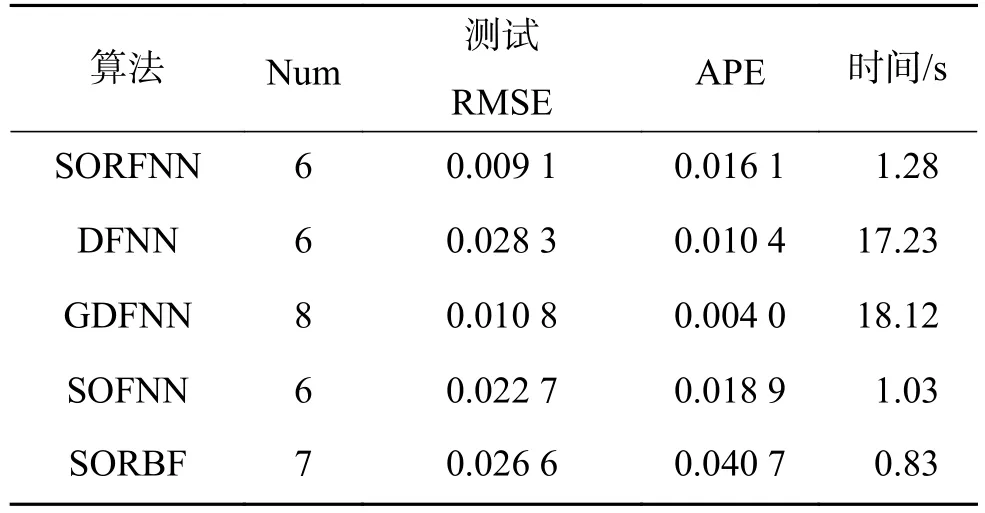
表 1 不同算法网络性能对比Table 1 Performance comparison of different algorithms

其中，均方根误差RMSE和平均百分比误差APE计算公式如下：

3.2 PM2.5浓度预测

通过非线性系统辨识实验，验证了所设计的SORFNN模型的有效性，接下来将该模型用于同样是非线性过程的实际PM2.5浓度的小时预测。

3.2.1 数据来源

PM2.5浓度预测和分析使用的数据一般有3种：地面监测站观测数据、同期同地区的气象观测数据、高空遥感图像。目前北京市已经建立了完善的空气污染监测站，因此本次实验选用易获得的地面监测站数据和同期气象数据，以北京市朝阳区某国控空气质量监测站为研究对象，采集该站点的小时监测数据。具体数据集来源于微软的城市计算项目[34]，该数据集采样时间为2014年5月1日—2015年4月30日，包含了4个季节的监测数据，样本内容丰富具有代表性，采样变量包括《环境空气质量标准》(GB3095—2012)中规定的6 项常规监测项目 CO、NO2、SO2、O3、PM2.5、PM10和气象变量温度(T)、湿度(RH)、风向(WD)、风速 (WS)、气压 (P)、天气 (W)，删除异常数据和缺失数据后获得4 000组完整数据。实验中先将样本数据随机化归一化处理，然后选择前3 000组用于网络训练并进行十折交叉验证，轮流将其中9份用作训练，1份作为测试，求其误差均值。后1 000组用于网络测试，并进行多次独立实验。这样训练样本和测试样本都包含了空气质量较好和较差时的观测数据，保证了样本的多样性。

3.2.2 特征提取

PM2.5的小时浓度与其他污染物和气象条件密切相关，陈冠益等[18]的研究表明PM2.5浓度受温度、相对湿度、风速风向、降雨的影响显著。Zheng等[19]的研究表明不同时刻的天气条件和SO2、NO2等污染物对PM2.5浓度影响较大。本文中选择当前时刻的污染物变量(CO、NO2、SO2、O3、PM2.5和PM10)、当前时刻的气象因子(温度、湿度、风向、风速、气压和天气)、下一时刻的预报气象因子(温度、湿度、风向、风速、气压和天气)作为特征变量。考虑到特征变量比较多，且各个变量之间有一定相关性，若直接引入神经网络预测模型会有信息冗余，造成模型复杂度变高，影响模型预测性能。所以，采用主成分分析方法进行特征变量提取，达到数据降维的目的。本文中取累计贡献率大于0.85的变量，最终提取出8个主成分作为神经网络预测模型的输入。

3.2.3 实验结果

实验中神经网络为8输入1输出，规则层初始神经元个数为4。预测模型的评价指标采用常用的均方根误差RMSE、平均绝对误差MAE、决定系数R2、一致性指数IA[7-8,28-29]。

式中：oi和分别是期望值和期望值的均值，pi和是预测值和预测值的均值。

图8给出了网络训练过程中规则层神经元个数的变化情况，从图中可以看出在训练过程中神经网络的结构是动态变化的，根据一段时间内样本的分布情况，神经元实现了增删调整，最终神经元个数为7个。图9给出了网络的测试效果，测试输出与期望输出拟合较好。图10是SORFNN与DFNN、GDFNN、SOFNN、SORBF方法的预测误差对比图，DFNN的误差在(–250,250)范围内，GDFNN和SORBF的误差都在(–150,250)之间，SOFNN 的误差范围是 (–100,250)，SORFNN的误差则在(–150,150)范围。相比其他方法，SORFNN的预测误差范围较小，分布也比较均匀集中。具体性能指标对比如表2所示。从表中可以看出，文中自组织方法有效地减小了预测模型的误差，在拟合度等方面也有所提高，是一种有效的自组织方法。

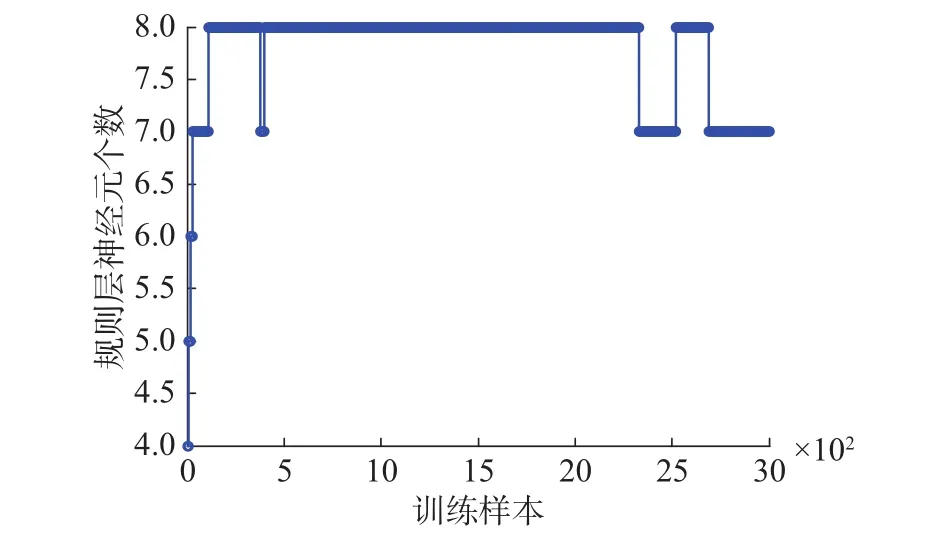
图 8 规则层神经元变化Fig. 8 Number variation of neurons in rule layer

图 9 测试效果Fig. 9 Test results

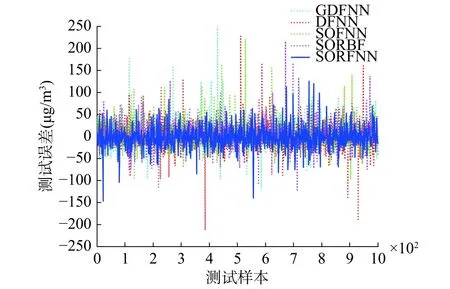
图 10 测试误差Fig. 10 Test error

表 2 不同网络性能对比Table 2 Performance comparison of different networks

4 结束语

通过分析PM2.5浓度变化的特点，本文提出采用自组织递归模糊神经网络来预测PM2.5浓度。经过PCA提取特征变量，实现数据降维和信息去冗余，有利于提高模型预测性能。为了解决神经网络结构优化问题，提出基于ε准则和偏最小二乘法的自组织方法，构建了自组织递归模糊神经网络模型，同时采用学习率自适应的梯度下降算法对神经网络的中心、宽度等参数进行训练，建立了PM2.5浓度预测模型。通过非线性系统辨识实验证明了该预测模型的有效性，最后将该模型用于实际问题PM2.5浓度的预测。实验结果表明该模型不仅能够获得较为精简的网络结构，而且预测精度有所提高，为PM2.5浓度预测提供了一种有效的方法。