中国象棋机器人棋子定位与识别方法

郭晓峰，王耀南，周显恩，尹阿婷，赵辉平，刘磊

（1. 湖南大学 电气与信息工程学院，湖南 长沙 410082; 2. 机器人视觉感知与控制技术国家工程实验室，湖南长沙 410082）

随着社会的不断发展和科技的不断进步，以中国象棋机器人为代表的娱乐服务型机器人，逐渐成为机器人研究领域的热点之一。

中国象棋机器人研究开始于21世纪初，2004年上海交通大学黄立波等[1]利用开放式控制器，成功开发了国内第一台中国象棋对弈机器人，同期多种对弈机器人相继诞生[2]。早期的中国象棋机器人棋子的定位与识别采用非视觉方式，如特制不同电阻值[3-4]或光敏电阻[5]的棋子与设计电子棋盘的方式进行棋子的定位与识别，类似地还可采用射频[6]等方法。这些非视觉的识别法都有：系统需特殊设计定制，适应性不强等缺点。随着机器视觉技术的发展，棋子的定位与识别也逐渐采用机器视觉的方法。

在棋子定位问题上：大多依靠棋盘间接定位，例如，许丰磊[7]对棋盘内90个小区域进行轮廓跟踪与提取，进而判断棋子位置；肖克先等[8-9]、杜俊俐等[10-11]通过对棋盘十字交点处进行检测。以上棋子定位方法均依靠棋盘直线检测或交点检测，无法做到脱离棋盘定位，且定位精度不高。

在棋子识别问题上：棋子识别实质就是字符识别，其研究相对比较成熟，但目前字符识别研究和应用最多的领域是汽车车牌的识别[12-13]。与传统字符识别不同，象棋棋子识别具有旋转任意性，目前针对中国象棋棋子字符的识别研究不多。冯元华[14]和莫妙桃[15]使用文字连通数、字符年轮统计等特征进行字符识别，但其需要预先对棋子字符进行特征统计，步骤繁琐且正确率基本在83%左右。随着计算机硬件和机器学习的发展，更多人尝试使用BP神经网络[16]、深度学习[17-18]等进行棋子识别。但机器学习或深度学习需要的训练样本大，训练时间长，实时性不强，更换棋子后同样需要重新训练，步骤复杂繁琐。

针对上述棋子定位中存在的依靠棋盘定位、定位精度不高等问题，本文提出了一种基于最小外接圆二次定位棋子定位方法，能够快速高精度实现棋子定位。针对当前传统文字识别方法识别率低，而基于机器学习的字符识别方法，存在训练时间长、实时性不强的问题，本文提出了一种旋转差分识别算法，实现棋子快速精准识别。

1 系统结构

我们自主搭建了象棋机器人的硬件平台，其结构示意图如图1所示。系统主要由URAM四轴机械臂及相连的摄像机、计算机、象棋棋盘和辅助光源组成，该系统可实现两个功能：1)开局阶段自动摆棋功能；2)人机对弈功能。该系统有两个工作区域：摆棋区域和棋盘区域。本文以摆棋区域内棋子的定位与识别进行研究。

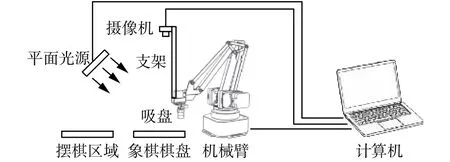
图 1 象棋机器人系统结构示意Fig. 1 Sketch map of chess robot system

2 定位与识别算法

本文算法整体流程图如图2所示。

图 2 算法整体流程图Fig. 2 The whole flow chart of the algorithm

2.1 一次定位与预处理

一次定位与预处理整体流程如图3所示。

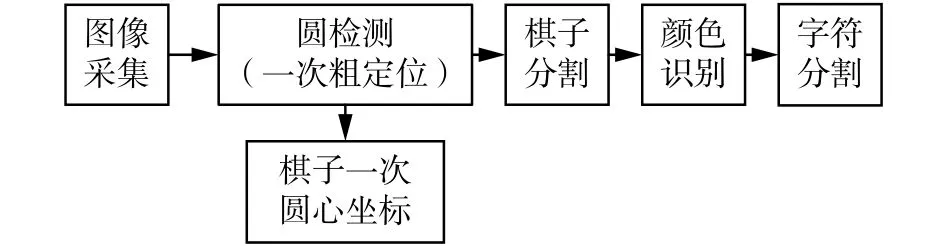
图 3 一次定位与预处理流程图Fig. 3 first positioning and pretreatment flow chart

首先对摆棋区域进行图像采集，本系统使用普通家用网络摄像头，图像分辨率为：1 280像素×720像素，测试所用棋子的直径为15 mm。

1)圆检测一次粗定位

棋子定位问题就是圆检测问题。圆检测算法主要有：最小二乘法[19-20]、多随机圆拟合度评估[21]等拟合方法。这类方法圆检测准确度高，运算量少，但其对噪声敏感，且不能一次检测多个圆。还有Hough变换[22]等投票(聚类)方法。这类方法将样本点映射到参数空间，用累加器或者类聚的方法来检测圆。这类方法对噪声不敏感，且可以一次检测多个圆，但其计算量大运算时间长。

本系统运行背景较复杂，有外界因素影响，因此需要圆检测具有较强的鲁棒性，且需要一次性检测出多个圆形。系统对于棋子的定位精度和识别准确度要求很高，但对于运行时间要求不高，因此综合以上考虑，本文使用Hough变换进行棋子一次粗定位。

对采集到图像进行Hough变换的粗定位，定位效果图如图4所示，并可得到粗定位圆心坐标。

图 4 一次定位图像Fig. 4 First positioning effect image

2)棋子分割

随后根据该定位坐标基于区域的图像分割将棋子前后景分离和棋子分割。

3)颜色识别

将RGB模型图片转换为HSV模型，随后对HSV模型中的各个值进行统计，寻找红、黑颜色的特征。

经过实验后得到：本文所使用棋子，红色H(H：hue)值范围为170～180；黑色H值范围为103～106，利用红色和黑色颜色的色调不同取值，就可将红色和黑色的棋子图像进行识别。

4)字符分割

由棋子图像的灰度直方图：由图5可知，棋子图像的灰度分布具有很大离散性，即棋子背景灰度值较集中为一种灰度值，黑色或红色字符集中为另一灰度值，且两者相差较大。

图 5 棋子图片直方图Fig. 5 The histogram of chess image

因此采用均值阈值分割进行二值化处理，首先计算图像像素灰度均值：T之后根据均值选定阈值进行分割：

式中K为比例系数。通过实验确定K取0.75时，字符分割效果较好。

2.2 棋子二次精确定位

系统工作环境较为复杂，干扰多，且所用棋子较小(仅为15 mm)，成像分辨率低。因此粗定位效果，部分棋子定位效果较差如图6所示。需要对棋子进行定位修正以确保定位精准。

图 6 定位效果Fig. 6 Positioning effect

本文提出的一种基于字符最小外接圆的定位修正方法的流程图如图7所示。

图 7 二次定位流程图Fig. 7 The flow chart of second positioning

二次定位算法步骤：

1)图片载入及预处理。由一次粗定位得到原始字符图如图8(a)，及粗定位圆心如图8中红色圆点表示。预处理得二值化字符如图8(b)。

图 8 二次定位中间过程图Fig. 8 Process image of second positioning

2)寻找最大轮廓。对二值化字符进行形态梯度运算如图8(c)。对形态梯度图进行轮廓提取，依次遍历所有轮廓并计算轮廓面积，保留面积最大的轮廓，如图8(d)所示。

3)寻找轮廓外接圆。由于圆具有稳定性和唯一性，因此寻找字符最大轮廓的最小外接圆如图8(e)，外接圆圆心如图中绿色圆点所示。

4)修正圆心。由最小外接圆，重新截取字符图片如图8(f)，保证字符位于图像中心位置，为后续识别工作做准备。同时由两次圆心坐标对比可得定位误差，并对粗定位圆心坐标进行修正，从而得到棋子精确的圆心坐标。

2.3 字符识别

棋子识别本质上就是字符识别，但不同于传统的字符识别，在摆放过程中棋子可能旋转任意角度，而造成字符倾斜，而传统基于像素的模板匹配识别不具有旋转不变性。如何克服圆形棋子的旋转特性是中国象棋棋子识别的难点。本文提出了一种旋转差分识别算法，其具体流程图如图9所示。

图 9 旋转差分识别算法流程Fig. 9 Flow chart of recognition algorithm

载入已制备模板图，将待识别图与其做像素差分如图10所示，并保留差分值。随后，将模板旋转a°后重复上述操作，直至360°旋转完毕为止。统计各个旋转角度的像素差分值，保留其中的最小值，记为Bn(n为模板序号，为1, 2,···,7)。

然后再和第2个模板进行上述操作。依次和所有7个模板进行上述操作后，则最小的Bn对应的字符，即为待识别棋子的识别结果，随即可得其对应的棋盘的位置。识别效果如图10所示。

图 10 识别效果Fig. 10 Recognition effect image

3 实验结果与分析

本系统硬件平台如图11所示，摄像机为普通家用网络摄像头，分辨率为：1 280像素×720像素。象棋棋子直径为：15 mm。计算机 CPU 为intel core i5—4 200 M，主频 2.5 GHz，通过软件开发平台Visual Studio 2012和Open CV2.4.9编写C + +程序，对棋子进行了定位与识别算法验证。

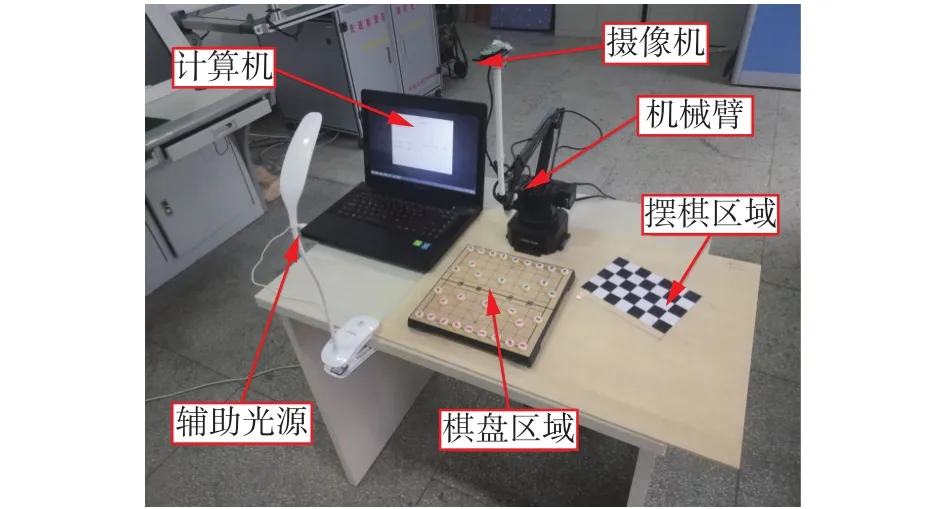
图 11 中国象棋机器人系统硬件平台Fig. 11 Hardware platform of Chinese chess robot system

3.1 棋子定位实验

利用本系统采集4张摆棋区域的图像，每张图片中包含32个棋子，共128个棋子。随后对每张棋子圆心进行人工标定，将检测定位坐标和标定坐标对比，得到定位误差，如表1 所示。

表 1 定位结果Table 1 Location result

两次定位误差为欧氏距离D，单位为像素(pixel)。定义误差修正率：

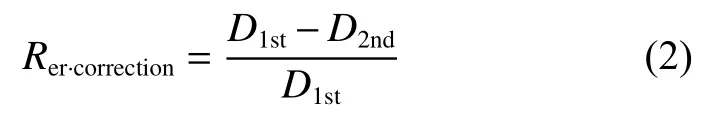
该参数可以反映定位精度的提升程度。由式(2)可知，定位精度提升均在40%以上，大部分在60%或70%以上，最高可达80%。

本系统使用棋子直径为15 mm，通过比例换算，可以得到最终实际定位误差。实验结果表明：棋子定位精度均在0.50 mm以上，最高定位精度达到0.11 mm，定位精准。棋子的平均定位时间为2.61 ms，定位快速，满足象棋机器人快速精准定位的要求。

各个字符定位精度存在差异：” 将”、“帥”、“炮”等的定位精度较高达到0.1 mm级别；而“士”、“車”的定位精度较低，仅为0.5 mm左右。因为相比于“将”、“帥”等左右结构分布的文字，“士”、“車”等为一体的竖长结构，造成其最大轮廓外接圆稳定性不足，定位存在较大偏差。

定位时间存在差异，“士”、“仕”定位时间短达到1.5 ms左右；而“馬”、“炮”等字符定位时间长为3.0 ms左右，这是因为：“士”、“仕”等字符的笔画较少的文字，“馬”、“炮”等较多，进行轮廓提取后字符轮廓数量多，轮廓遍历时遍历的次数多，而造成定位时间长。

3.2 棋子识别实验

本文采用旋转差分识别算法，因此棋子识别率和差分时模板每次旋转角度a密切相关，且算法的运算时间也与其直接相关，a越小，即识别率越高但运算效率越差。如何平衡识别率和运算效率，是该算法要解决的关键问题。

采集20副图像共640个棋子进行测试，在0°～45°区间内分别设定了不同的差分旋转角度a°进行11次实验，如表2 所示。注：运算时间为单个棋子的全流程平均运算时间，包括定位与识别。

表 2 识别结果Table 2 Recognition result

由表2可以得到棋子识别率和运算时间与差分旋转角度a的关系图，如图12和图13所示。

图 12 识别准确率Fig. 12 Recognition accuracy

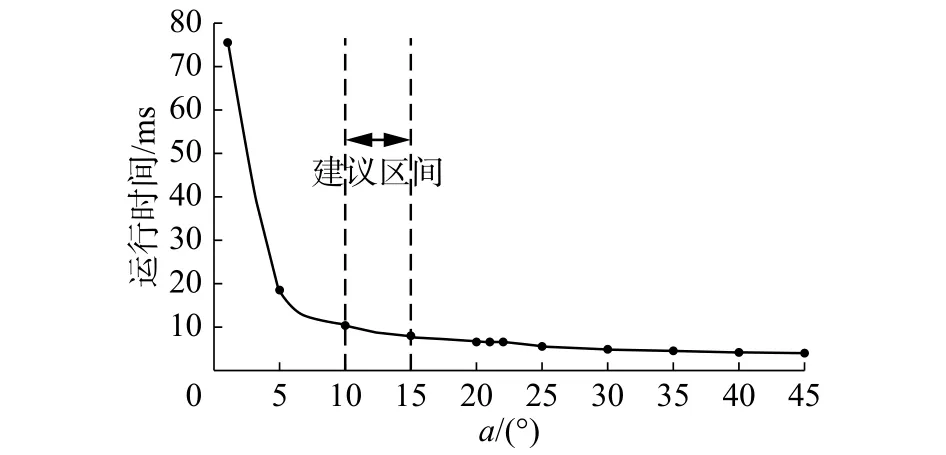
图 13 运算时间Fig. 13 Operation time

对图12、13进行分析，从识别率来看，当旋转角度在1°～21°变化时，系统均保持较高的准确率，达到98%。当角度超过21°以后，准确率开始下降并且下降速率越来越快。

从运算时间来看，角度为1°时处理一个棋子平均耗时75.6 ms。但随着角度不断增大，运算时间迅速减小，为5°时，运算时间已减小到18.7 ms。随后减小速率不断放缓。

综合识别率和运算时间分析，该系统差分识别算法的旋转角度选择10°～15°较为适宜。在此角度范围内，棋子识别率较高为98%左右，全流程运算时间为10 ms左右，满足象棋机器人系统的要求。

选定旋转差分角a=13°，对20幅图片中各个字符识别情况分别统计如表3所示。其中错误识别为：“炮”错误识别为“相”；“馬”和“兵”之间错误识别；“車”和“卒”之间错误识别。字符之间相互错误识别的原因和如何进一步提升算法的识别准确率是下一步研究的重点。

3.3 实验结果对比

将本文在旋转差分角度设定在13°情况下的实验数据与文献[17]的实验数据进行对比，得到结果如表4所示。

表 3 旋转差分角为13°时的识别结果Table 3 Recognition results when the angle is 13 degrees

表 4 对比测试结果Table 4 Comparison of test result

从表4可知，本象棋棋子定位与识别系统棋子定位误差0.5 mm略低于文献[17]的0.8 mm，识别准确率98.8%略高于文献[17]的98%，该两项指标相差不大。但本系统棋子全流程运算时间仅为9.3 ms，远远小于文献[17]的最短识别时间49 ms。

本文使用的摄像机为普通网络摄像头分辨率为1 280像素×720像素，文献[17]使用的是工业高清相机分辨率为1 000像素×1 000像素；本文使用的棋子为直径15 mm，文献[17]使用的棋子直径为28 mm；且文献[17]的测试环境较为简单，为测试平台箱内部，本文的测试环境较为复杂。因此，本文的综合测试效果优于文献[17]，具有良好的应用前景。

4 结束语

本文针对中国象棋机器人中棋子视觉定位与识别问题，提出了一种基于最小外接圆二次定位的定位方法和一种旋转差分识别算法。实验结果表明该定位方法能够实现棋子的快速高精度定位，定位精度达到0.5 mm，平均定位时间为2.6 ms；能够快速精准地识别棋子，在保证棋子识别准确度达到98%以上的情况下，单棋子全流程运算时间为10 ms左右，完全满足现有象棋机器人的指标要求。

目前该算法在个别字符定位误差和识别准确度、棋子定位时间、棋子全流程运算时间等方面存在进一步优化空间，这将是下一步研究的重点。