基于电源灵活性裕度的含风电电力系统多源协调调度方法

苏承国, 申建建, 王沛霖, 周凌安, 程春田

(1. 大连理工大学水电与水信息研究所, 辽宁省大连市 116024; 2. 黄河水利职业技术学院, 河南省开封市 475004)

0 引言

近年来,以风电为代表的可再生能源实现了快速发展[1],截至2016年底,中国风电并网规模已突破148.6 GW,占全国发电装机容量的比重超过9%[2],风电已成为电网中非常重要的清洁能源。然而,由于风电的随机性、间歇性和反调峰[3]特性,风电大规模并网极易导致火电机组在日内频繁启停或运行于深度调峰状态,给电网实际调度运行带来极大挑战,也在很大程度上制约了风电进一步消纳。因此,在含风电的电力系统中建立多源相济协调调度机制,充分发挥灵活性电源的调节能力和电源之间的互补特性,对于应对风电不确定性问题、提高风电接纳能力显得尤为必要。

关于风电与其他电源的协调调度问题已有诸多文献报道[4-11],主要是利用风电与水电、气电、火电、抽水蓄能、储能等常规能源的互补特性,同时配置较为充裕的备用容量,以缓解风电接入对系统安全稳定运行的不利影响,但这种方法比较适用于风电比例较小的情况,当电网中风电规模较大时,风电功率频繁波动会导致电网净负荷波动更为剧烈,单纯依靠备用容量难以有效响应净负荷的快速变化,电网安全往往面临较大风险;另一方面,配置足够的备用极易造成大量的备用冗余,成本昂贵且难以为继。近些年,部分研究从系统灵活性的角度对高比例可再生能源系统运行问题进行了分析[12-15],并提出灵活性裕度的概念以全面评估电力系统对可再生能源的消纳能力,但目前对于灵活性的研究大多以原理分析和定性评价为主,仍缺乏实用的电力系统灵活性量化评价指标和建模方法。文献[16]提出了一种灵活性评价指标及相应计算方法,但未考虑系统不确定因素，如机组随机停运、风电预测误差等,在很大程度上限制了工程实际应用。

本文将灵活性理论和电力系统多源协调调度问题结合起来,提出一种基于电源灵活性裕度的风水气火多源协调调度方法。首先,参考电力系统灵活性定义,综合考虑各类电源的运行特性,以及负荷和风功率的波动性和随机性影响,提出了电源灵活性裕度的工程量化评估方法。然后以污染物排放总量最小为目标,引入上调灵活性和下调灵活性约束,构建了多源协调优化调度模型,并提出了分层调度求解策略,实现了系统运行可靠性与风电利用效益的有效协调。最后,通过编制某省级电网短期调度方案验证了本文方法的合理性与有效性。

1 电源灵活性裕度指标

电力系统灵活性,是指在一定时间尺度下,电力系统通过优化调配各类可用资源,响应(净)负荷波动和可再生能源随机变化的能力[12]。电力系统灵活性实际上是一个范围很广的概念,包含了电源侧、负荷侧、电网侧、储能装置等各个方面,完备的灵活性指标应该将这些方面全部包含其中。但考虑到目前中国电网中的需求侧响应技术和大规模储能技术尚未推广,较为完备的灵活性定量评价指标在现阶段往往不具备实用性和可操作性。因此,本文重点考虑了电源侧的灵活性指标,旨在从电源侧衡量电力系统应对大规模风电并网的能力,因而后文的“灵活性”主要是指电源灵活性。本节在已有研究的基础上,从灵活性供需平衡的角度提出了电源灵活性裕度指标及其定量计算方法。

抽水蓄能电站在电网中的装机比重很小,核电机组基本以固定出力运行,供给侧主要依靠水电、气电、火电等常规电源实现灵活性调节。所有常规机组在各个时段的可调容量之和即为系统在该时段能够提供的灵活性调节容量,针对负荷上升和下降的情况,分别称之为上调灵活性和下调灵活性供给,表示为:

(1)

(2)

系统灵活性需求源自负荷及风电的波动性和不确定性、机组强迫停运等,因此针对负荷上升和下降的情况,上调灵活性需求和下调灵活性需求分别为:

(3)

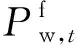
根据以上对灵活性供给和需求的描述,将电源灵活性裕度指标定义为灵活性供给与灵活性需求的差值,相应的,灵活性裕度也具有向上和向下两个方向,即

(4)

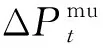
需要说明的是,由式(1)至式(4)可以看出,系统需配置的灵活性调节容量实际上包含了爬坡容量和旋转备用容量两部分,因此,系统旋转备用容量可视为灵活性调节容量的一部分,在安排调度计划时电源灵活性裕度满足则系统正负旋转备用约束必然满足。

2 数学模型

2.1 目标函数

与水电和燃气机组相比,电网中火电机组在运行过程中会排放出较多对环境有害的SOx,NOx及粉尘等污染物[17]。随着近年来环境污染的加剧,世界各国都不断加强对污染物排放的控制,大力促进风电等清洁能源的发展便是其重要举措之一。因此,为了体现风电并网的环境效益,本文以系统在调度期内污染气体综合排放总量最小[18]为目标函数,表示如下:

ζmtexp(λmtPmt,t)]

(5)

式中:F为污染气体排放量;αmt,βmt,γmt,ζmt,λmt为火电机组mt的污染物排放量系数,可通过机组的实际排放数据拟合得到;T为调度周期。

2.2 约束条件

多电源协调优化调度需要同时考虑电网相关约束以及各类型电源实际运行特征,下文将详细介绍。

2.2.1电网约束

1)系统功率平衡约束

(6)

2)上调灵活性约束

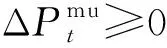
(7)

3)下调灵活性约束

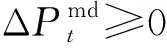
(8)

2.2.2电站(机组)运行约束

2.2.2.1 水电站约束

1)上下游水库水力联系

Imh,t=Qmh-1,t-τ+IR,mh,t-Smh-1,t-τ

(9)

式中:Imh,t为水电站mh在t时段的入库流量;τ为电站mh-1和mh间的水流滞时;Qmh-1,t-τ为电站mh-1在t时段的发电流量;IR,mh,t为水电站mh-1和水电站mh间的区间流量;Smh-1,t-τ为水电站mh-1的水库在t时段的弃水流量。

2)水量平衡约束

Vmh,t=Vmh,t-1+3 600(Imh,t-Qmh,t-Smh,t)Δt

(10)

式中:Vmh,t为水电站mh在t时段的库容;Δt为时段步长。

3)库水位约束

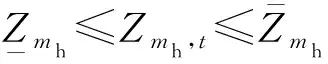
(11)

4)末水位控制

Zmh,t=Zmh,end

(12)

式中:Zmh,end为电站mh在调度期末水位控制值。

5)出库流量约束

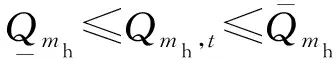
(13)

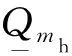
6)电站出力上下限约束

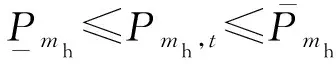
(14)

7)电站爬坡能力约束

(15)

2.2.2.2 燃气机组约束

1)机组日电量控制

由于中国天然气行业尚处于发展初期阶段,基础建设不足导致气量常不能足额供给,因此在实际调度中一般会设置燃气机组的日控制电量,即

(16)

式中:Emg为燃气机组mg的日控制电量。

2)机组出力上下限约束

理论上燃气机组运行可极为灵活,能在0～100%的负荷率区间内运行。但相关研究[4,19]表明,当燃气机组负荷率在75%以上时,其发电效率高、气耗率低、污染物排放水平也较低,在此运行区间内负荷率的变化对机组安全经济运行的影响相对较小。然而当机组负荷率低于75%时,其各项性能会显著降低,发电成本也急剧增加,会极大地损害燃气电厂的发电效益。因此,本文将75%的负荷率设置为燃气机组稳定运行的出力下限,即

(17)

3)最小开机持续时间约束

频繁启停会显著影响燃气机组的使用寿命,机组的运行成本也将大大增加,因此,通过设置最小开机持续时间以尽量避免机组的频繁启停,即

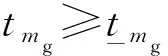
(18)

除上述约束外,燃气机组还包括机组出力爬坡约束,处理方法与水电站类似,不再赘述。

2.2.2.3 火电机组约束

1)开停机状态约束

目前,能耗较小的大型火电机组是电网中的发电主体。大型火电机组从锅炉处于冷备用状态到并网需要1～2 d,考虑到调度指令因素,此时间可能会更长。因此,本文模型不考虑火电机组的日内启停[20-21],即机组运行状态一旦确定,在日内不会发生变化,即

umt,1=umt,2=…=umt,t=…=umt,T

(19)

式中:umt,t为t时段机组开机状态的0-1整数变量。

2)火电机组其他约束,如出力上下限约束、机组爬坡能力约束,表示方法与水电站类似,不再赘述。

3 求解方法

3.1 总体求解思路

风水气火多源协调调度是一个异常复杂的混合整数非线性规划问题,当系统规模较大时,直接优化求解的难度很大。为了减小问题解搜索空间,提高求解效率,本文借鉴了文献[7-8]介绍的分层求解思想,将模型分解为风电、水电、气电、火电4个调度层,调度层之间以负荷和灵活性裕度为关联,同时针对各电源运行特性和电网调度需求,分别设计了适合的求解方法。图1给出了总体求解框架,其求解思路是:依据风电优先、全额上网的政策,风电尽可能地全额消纳,不再作为调度中的优化变量,若后续计算中系统下调灵活性不足,则采取一定的弃风措施,并修正净负荷曲线;水电、气电机组运行灵活,污染物排放极少,应优先承担电网调峰任务,尽量削减净负荷峰谷差以提升系统灵活性裕度,同时确保余留给火电的净负荷尽可能地平坦,平稳的负荷过程对于火电机组平衡系统负荷、减少其污染物排放尤为重要;火电机组调节能力相对较差,因此应尽可能地承担基荷。在求解过程中,针对常规水电、气电优化调度层,分别采用变尺度优化方法、改进的日启停调峰运行方法进行求解;针对火电优化调度层,先利用启发式搜索方法确定火电机组组合,然后采用改进粒子群优化(improved particle swarm optimization,IPSO)算法确定该机组组合方式下的机组最优出力过程。需要说明的是,虽然分层求解策略求得的调度结果只是较优解或局部最优解,但是该策略计算效率较高,得到的调度方案比较符合各电站/机组的实际运行工况和电网的调度习惯,具有很强的实用性。考虑到风电不作为优化变量,下文将重点介绍水电、气电和火电调度层的求解策略。

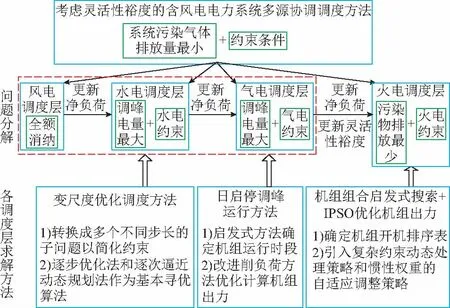
图1 总体求解框架Fig.1 General framework of solution

3.2 水电调度层

有关水电短期调峰问题的求解方法已有大量研究报道,本文采用变尺度优化方法求解该问题,其详细的求解步骤可参考文献[22]。

3.3 气电调度层

在现阶段,由于天然气供应不足、发电成本过高等原因,燃气机组采用昼开夜停的日启停运行方式。本节针对当前电网中燃气机组运行现状以及燃气机组运行特性,提出一种改进的日启停燃气机组调峰运行方法。对于燃气机组mg,其求解过程如下。

1)确定机组开机时段

根据机组的日计划电量、出力上下限约束以及最小开机持续时间要求,采用式(20)至式(23)计算机组所有可行的运行时长(稳定运行阶段,不包含机组启停阶段)。

Emg,peak=Emg-Emg,on-Emg,off

(20)

(21)

(22)

(23)

为确保机组在负荷高峰时段发电,充分发挥机组调峰作用,搜索机组mg面临的净负荷(扣除风电、水电出力之后的负荷)均值最高的tmg,n个时段,作为机组的可行连续开机时段,n个可行连续开机时段可构成集合,即

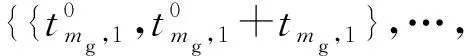
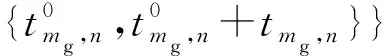
(24)

2)优化机组出力

如前文所述,对于燃气机组优化调度层,以系统调峰为优化目标,为此,采用电网净负荷方差最小做目标函数为:

(25)

式中:Ct′为扣除风电、水电出力之后在t时段的净负荷。

通过该方法得到燃气机组出力可兼顾电网调峰需求与机组运行限制(如调峰深度、运行时长、出力波动约束),充分发挥机组的灵活性调节能力。

3.4 火电调度层

如前文所述,当前电网中火电机组完成一次启停的时间较长,难以在日内完成开停机状态转换。基于以上运行特点,为了减少寻优空间和计算冗余,本节将火电优化调度层分解为上下2层依次进行求解:上层采用启发式的优先顺序法决策机组开机方式;下层采用IPSO算法确定该机组组合方式下的最优出力过程。

3.4.1确定机组组合方式

确定火电机组组合方式的启发式搜索步骤如下。

1)依照单位污染物排放量由低到高对火电机组进行排序,单位污染物排放量相同时,比耗量系数低的机组优先,建立机组开机排序表。比耗量系数定义为:

(26)

2)剔除排序表中的检修机组、电量超发或即将超发机组和尚处于停机状态并且未达到最小停机时间要求(以d为单位)的机组。

3)依据机组排序表中的顺序,逐次累加各机组最大出力,直至满足最高净负荷及其正备用需求:

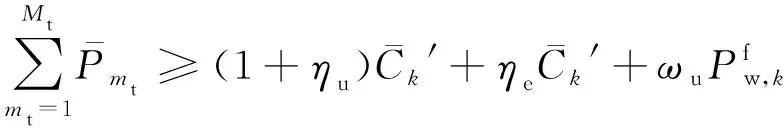
(27)

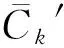
4)采用式(28)进一步验证机组最小出力能否满足最低负荷点的负备用要求,若不满足,说明在负荷最低点时系统难以完全消纳风电,需要在负荷最低点附近采取弃风措施,直至约束满足。

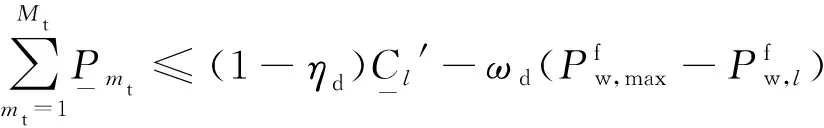
(28)

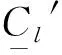
3.4.2优化机组出力

粒子群优化(particle swarm optimization,PSO)算法在电力系统优化调度领域得到了广泛应用。本节针对传统PSO算法在求解具有复杂约束问题时存在可行解获取困难、易于陷入局部最优解等弊端,提出一种耦合复杂约束动态修补策略的IPSO算法,用于优化求解机组出力。

该策略的主要思想为:在获取初始解和每次迭代更新时,对不满足约束条件的粒子进行修正, 使其尽量满足约束条件,对于部分难以修正的约束,采用罚函数法转化为无约束优化问题。具体的修补原则如下。

原则1：调整机组出力使其满足机组出力上下限约束。

(29)

原则2：如果违反机组爬坡速率约束,则按以下原则调整。

(30)

原则3：当t时段违反功率平衡约束时,计算功率偏差值。

(31)

若ΔPt>0,标记t时段出力值达到下限的机组序号(假设为k),按照式(32)将功率偏差值分配到各个机组;若ΔPt<0,标记t时段出力值达到上限的机组序号(假设为n),按照式(32)将分配功率偏差值。

(32)

在分配完成后如若违反出力上下限和爬坡速率约束,按照原则1和2调整机组出力。反复调整机组出力,直至ΔPt=0或r=Rset(r为截至当前的调整次数,Rset为设定的最大调整次数),则停止迭代。

如果达到设定的调整次数, 仍然不能满足功率平衡约束,说明该粒子本次迭代得到的解并非可行解(但已经尽量靠近了可行解区域)。同样,上调和下调灵活性约束也难以同时满足,因此,本文在适应度函数中加入功率平衡约束和系统灵活性约束的罚函数,保证在下次迭代时将粒子尽可能吸引到可行解的区域中。相应的适应度函数为:

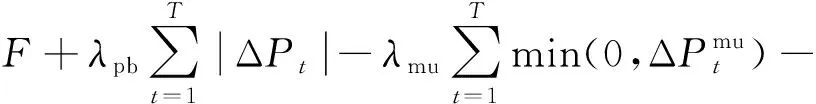
(33)

式中:λpb,λmu,λmd分别为功率平衡约束、上调灵活性约束和下调灵活性约束的惩罚因子。

若迭代至最后一代时,功率平衡约束或系统灵活性约束仍不满足,则搜索灵活性不足的时段并采取弃风措施,以保障电网安全运行。

关于PSO算法的其他具体步骤请参见文献[24]。

4 实例分析

4.1 工程背景

以中国某省级电网冬季典型日的短期调度方案制作为例,验证本文模型和方法有效性与可行性。

算例包含10个大型风电场、2个梯级水电站、10台燃气机组和36台火电机组(1 000 MW机组4台、 660 MW机组4台、600 MW机组10台、350 MW机组4台、330 MW机组6台、300 MW及以下机组8台)。以1 d为调度周期,1 h为1个调度时段。调度周期内系统负荷和风功率预测数据如附录A表A1所示,负荷与风电预测出力曲线如附录A图A1所示,由图A1可以看出,风电预测出力呈现出一定“反调峰”特性,增加了调度运行的难度。水电站和燃气机组的运行参数分别见附录A表A2和表A3,部分火电机组的运行参数如附录A表A4所示。其他参数ηu=ηd=5%,ηe=8%,ωu=ωd=25%,IPSO算法最大迭代次数取500,粒子数目取50。

4.2 计算结果及分析

采用JAVA语言编制了本文方法的应用程序,在主频2.3 GHz、四核CPU、内存16 GB、硬盘500 GB的Lenovo计算机上连续运行该算法50次,得到的最优值和最差值的偏差仅为0.34%,并且完成一次计算的最长时间为42.6 s,可有效满足电网短期调度的时效性要求。图2和图3分别为风水气火协调优化调度结果和电网实际调度结果,两种场景下均实现了风电全额消纳。

从图3可以看出,水电站和燃气机组在系统负荷高峰时段(10:00—22:00)加大出力,在负荷低谷时段不发电,利用其灵活的调节能力,达到平抑风电随机波动和削减负荷峰谷差的目的,确保余留给火电机组的负荷尽可能平稳。经过水电、气电有效调峰,剩余最高负荷(即火电承担的最高净负荷)为13 911 MW,负荷峰谷差由8 142 MW削减为6 214 MW,负荷均方差由2 874 MW削减为2 265 MW,证明了本文水电、气电优化层的求解策略的有效性。实际调度方案中,由于对水电站运行模型进行了简化,因此安排水电站在16:00—21:00定出力运行,同时安排燃气机组在负荷高峰时段满功率运行,这种运行方式虽然也有效降低了负荷峰谷差(峰谷差削减为6 763 MW),但由于定出力运行,限制了水电和气电的调峰潜力,在10:00—22:00期间余留给火电的负荷仍然有较大波动。

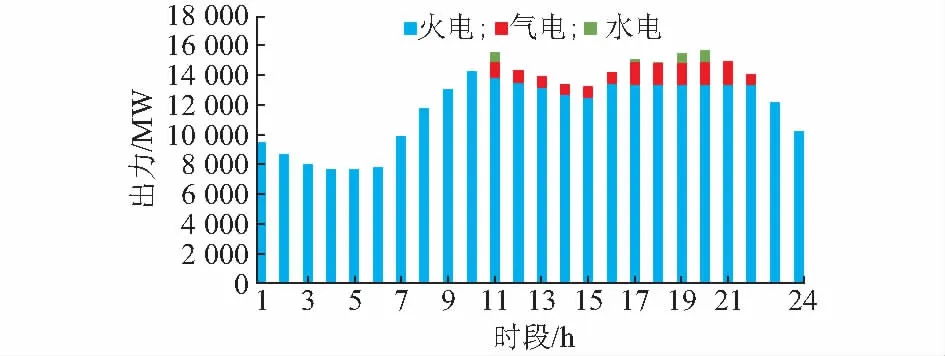
图2 协调优化调度结果Fig.2 Results of coordinated optimal dispatching

图3 实际调度结果Fig.3 Results of actual dispatching

但同时也应该看到,经过优化调度后,火电机组在调度期内出力波动依然较为明显,主要是因为:水电、气电装机比重相对较小,并且正值枯水期,来水量偏少,使得水电站可发电量较少,而燃气机组由于天然气供应不足和自身发电成本限制,也大大影响了其灵活性的发挥。未来随着“西气东输”工程全面实施和电网中燃气机组装机比重不断增加,气电作为灵活性电源在电网中的作用将愈加显著。

将本文优化调度后的结果与该日电网实际调度运行(风电全额并网,备用容量取为最高负荷的固定比例)的结果进行比较, 图4(a)和图4(b)分别为实际调度和本文优化调度的系统上调灵活性裕度和下调灵活性裕度,可以看出,电网实际调度在负荷高峰时段存在大量灵活性(正备用)冗余,而在负荷低谷时段下调灵活性裕度存在不足,在02:00—05:00的灵活性缺额分别达到了128，350，420，251 MW,意味着在这些时段电源的下调能力不足,可能无法快速响应负荷和风功率预测偏差,发生弃风或火电紧急停机的风险较高。而优化调度结果由于在负荷低谷及其相邻时段考虑了系统下调灵活性需求,然后在负荷高峰时段充分利用了水电、气电的上调灵活性优势,使得系统在各个时段均满足灵活性裕度需求。

图4 优化前后灵活性裕度对比Fig.4 Comparison of flexibility margin between before and after optimal operation

统计优化调度后全天的系统污染物排放总量、火电开机台数和开机容量,并与实际调度场景做对比,结果如表1所示。

表1 本文方法与电网实际运行污染物排放对比Table 1 Comparison of pollutant emission between actual operation and the method in this paper

由表1可见,通过对各类型电源出力和备用容量获取方式的优化,在保证风电完全消纳和满足系统灵活性要求的前提下,系统仍然存在污染物减排空间,相对于实际调度场景,排污染排放减少量为341 t,减排率为4.1%。同时,随着系统火电开机容量的大幅降低,使得火电机组在调度周期内的负荷率得到有效提升,进而可达到提高机组运行效率、降低发电煤耗的效果。这一结果主要受益于两个方面:一方面是本文模型引入了电源灵活性指标,对有限的灵活性资源进行了优化分配,大大减少了系统正备用冗余,从而减少了开机机组台数;另一方面是利用了分层求解的思想,针对水电、气电优化调度层分别设计了合理有效的求解方法,最大限度地发挥了其灵活性优势,然后采用IPSO算法实现了火电机组最优负荷分配,避免了PSO算法陷入局部最优解。

由于短期风功率预测技术的限制,风电的日前预测出力和实际出力间必然存在一定的偏差。本文将进一步地考虑风电预测偏差对优化调度结果的影响,验证优化调度结果对系统中不确定性因素的适应性,即所提模型和方法的鲁棒性[25]。

附录A图A2为该日实际的风电出力过程,虽然总体趋势与预测出力过程相近,但在系统负荷低谷时段(04:00—08:00),实际出力要明显高于预测出力,极大地增加了风电低谷消纳的难度。

严格来说,日前制作的调度方案根据实时风功率进行调整时,更多的是属于实时调度的范畴,为了简化计算,本文根据实际的风功率和负荷曲线,固定日前确定的火电机组的开机方式,使用上文介绍的方法重新计算得到了新的调度方案,新的调度方案可近似认为是调整方案,调整后的结果如附录A图A3所示。从图A3可以看出,水电和气电出力在高峰时段根据净负荷的变化趋势及时做出了调整,使得余留给火电的净负荷继续保持平稳,同时为了应对风电在低谷时段的出力突增,部分火电机组在低谷时段降低出力,以接近最低技术出力运行,以保证风电的全额消纳。调整后的调度方案能够重新达到系统功率平衡,验证了本文方法得到的调度方案的鲁棒性。

附录A图A4为优化调度方案调整后的电源灵活性裕度,可看出在实际运行场景下,电源上调灵活性仍存在一定的裕度,但下调灵活性在03:00和04:00已经分别出现了184 MW和320 MW的缺额,表明此时系统中电源的下调灵活性已经达到了极限。随着风电渗透率的不断提高,电网面临的灵活性不足问题将成为限制风电消纳的主要瓶颈之一。因此,在电力系统规划中,应进一步提高电源结构中抽水蓄能、燃气电站等灵活性电源的比重,全面提升电力系统的灵活性以适应高比例可再生能源的运行。

5 结语

本文提出一种基于电源灵活性裕度的含风电力系统多源协调优化调度方法,并将其应用于中国某省级电网的日前发电计划编制,通过实例分析,获得如下结论。

1)提出的电源灵活性裕度指标充分考虑了风电和负荷的波动性和不确定性影响以及水电、气电和火电的灵活性调节能力,可有效评估系统的风电消纳能力,可实现有限灵活性资源的优化分配,大幅减少系统备用冗余,提升机组的负荷率和运行效率。

2)本文方法利用水电、气电灵活性的调节作用有效平抑了风电和负荷的随机波动,并且进一步优化了火电机组的出力过程,在保证风电完全消纳和满足电网灵活性需求的同时,降低了系统的污染物排放水平。

3)通过发电侧多源协调互济是提高电网对间歇性新能源接纳能力的一种有效实用的技术手段,本文提出的风水气火多源相济协调策略,可为大规模风电接入后电网发电调度运行提供借鉴和参考。

高比例可再生能源将成为电力系统未来发展的一个突出特征,因此从灵活性角度看待电力系统运行问题显得尤为必要。本文重点研究了电源灵活性裕度指标以及基于该指标的多源协调调度机制,暂时未考虑网络安全约束,下一步的研究计划是在本文提出模型的基础上加入网络约束,使得建立的多源协调调度模型更符合实际。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

苏承国(1994—),男,博士研究生,主要研究方向:电力系统优化运行、大规模清洁能源消纳技术。E-mail： suchguo@163.com

申建建(1984—),男,通信作者，博士,副教授,主要研究方向:水电及电网调度。E-mail: shenjj@dlut.edu.cn

程春田(1965—),男,博士生导师,长江学者特聘教授,主要研究方向:大水电系统调度、清洁能源电力市场、电网调度与控制等。E-mail: ctcheng@dlut.edu.cn