计及低频采样用电量信号的电器运行情况识别方法
吴烁民, 张凯锋, 王 颖, 李亚平, 黄宇乾
(1. 复杂工程系统测量与控制教育部重点实验室(东南大学), 江苏省南京市 210096; 2. 中国电力科学研究院有限公司(南京), 江苏省南京市 210003)
0 引言
电器运行情况识别(EOI)是负荷分解的一个重要研究方面。负荷分解通常是利用电力入口处的总用电信息对其内部各用电设备进行状态监测与能耗分解;EOI则侧重于识别电器的启停情况。EOI技术有助于构建用户行为模式,这对电力供给方实现更精细的需求侧响应及电力用户了解自身电能消费,降低用电成本均有重要意义[1]。
目前,以非侵入式方法进行负荷分解受到了很大的重视。自Hart[2]起,国内外大量学者基于高频(采样频率超过10 Hz)负荷采样数据,利用其丰富的负荷特征实现负荷分解:文献[3-4]利用有功暂态特征对投切负荷进行辨识。文献[5-6]将负荷分解问题转化为由混合电流信号分解出各负荷独立电流问题。文献[7-9]利用了高频采样下的电流信号、电流的谐波信号以及有功功率特征,完成了负荷分解。
以上方法可以实现精度较高的负荷辨识,但目前大量使用的智能电表,受限于制造成本、传输能力、存储成本等因素,采样间隔较大。例如:Eagle智能电表采样间隔为8 s,英国智能电表采样间隔为10 s[10]。国内智能电表采样间隔通常为10 min级[11-12]。在低频采样下,负荷的有功功率、电流暂态特征等已丢失,上述方法难以实施。
为此,有学者尝试针对低频采样(采样频率不超过1 Hz)负荷分解问题进行研究。文献[13-14]将总负荷有功序列分割为单负荷或多负荷同时运行的子序列,再以动态时间弯曲(dynamic time warping,DTW)距离为相似性量度指标确定识别结果。DTW距离对于局部的幅值差异、序列长度等不敏感,广泛应用于序列间的模式识别中[13-15]。Dinesh等人利用Karhunen-Loeve变换增强各负荷有功稳态特征间的差异性,采用基于最大后验估计的方法完成负荷分解[16-18];文献[10]从多方面对整数规划(IP)进行改造,使其对于低频采样数据有较好的适应性。文献[19]利用负荷有功、无功稳态特征,将负荷分解问题转化为求解最优状态组合的阶乘隐马尔可夫模型(FHMM)解码问题。
尽管上述研究均基于1 Hz以下采样频率的负荷信息,但与国内电表的实际采样间隔仍有较大差距。10 min级的负荷采样数据为一种超离散数据,由于其信息量极低,难以直接对其进行分析研究。目前鲜有基于10 min级采样数据做负荷分解的研究,未见基于10 min级采样数据专门做电器启停情况分析的研究。例如,文献[16-18]的方法无法基于10 min采样数据建立负荷本征子空间,其负荷分解方法难以直接应用;文献[14]结果表明,当采样间隔由1 min改为4 min时,该方法对多负荷序列识别准确率已由85%降至73%以下;文献[13,19]建立FHMM需要大量训练样本,计算成本高。本文认为,若能扩充10 min级负荷采样数据的信息量,就能采用现阶段较为成熟的负荷分解方法对其进行分析研究。
本文认为用电量信号可用于扩充此种超离散数据的信息量,且10 min级的有功功率值和用电量信号均易于获取[11-12]。因而,本文提出一种计及用电量信号的EOI方法。该方法针对采样间隔为10 min的有功数据,利用10 min内的用电量重构负荷采样数据,丰富了负荷特征,为EOI提供便利。本文提出的方法所需数据容易获得,且无须大量训练样本,为低频负荷分解方法提供了一种新的思路。
1 计及用电量信号的EOI方法整体思路
现有的负荷分解算法均直接针对采样数据,若有负荷设备在采样点间投切,抑或在采样点间改变运行状态后复原,此时仅依据采样点处的数据难以复原该过程。而本文所提出的计及用电量信号EOI方法,结合采样点间的用电量信号,估计采样点间有功功率波形趋势,为进一步负荷分解提供便利。
本文所提的算法主要分为两个阶段。
1)基于用电量信号重构总有功功率曲线:利用用电量信号,估计采样点间有功功率曲线走势。构造一条曲线将采样点处各总有功功率值连接起来。本文将这一过程称为“总有功功率曲线的重构”。显然,重构所得有功功率曲线较总有功采样数据拥有更多的信息量。总有功功率曲线的重构方法示意图如图1所示。
图1中,黑色实心点A为第i个采样点,B为第i+1个采样点。Pi表示第i个采样点的纵坐标值,ti表示第i个采样点的横坐标值。若采样间隔为10 min,则ti+1-ti=10 min。A和B是固定点。空心C点为重构曲线上的一个动点,虚线即重构的总有功功率曲线。重构的总有功功率曲线与t轴围成的面积与A和B点间用电量值相等。

图1 总有功功率曲线的重构方法示意图Fig.1 Schematic diagram of reconstructing total active power curve

两阶段流程图详见附录A图A1。需要说明的是,本文中出现的负荷状态是指家用电器某一工作状态所对应的有功功率值。
重构总有功功率曲线在数学上存在多解,但总有功功率曲线的重构是为EOI提供便利,因而在具体求解时可以根据采用的负荷分解方法、负荷状态等对问题解做限定,以保证该问题解的唯一性。由于本文采用的是基于IP的负荷分解方法,因此本文需要将负荷采样得到的总有功数据重构为一连串的方波信号。
2 计及用电量信号的负荷数据重构
由于本文是基于IP的负荷分解算法,因此需要将负荷总有功功率曲线重构为方波。而方波的幅值为若干电器设备处于稳定工作状态时对应的有功功率值的叠加。因而,本文首先描述了各电器稳态情况。
本文算法基于以下两个基本假设:①家中包含的电器设备种类、数目已知;②各电器设备非零稳定工作状态对应的有功功率值已知。
需要说明的是,上述两条基本假设所需数据均可通过现有文献提出的方法获取,因而不影响大规模应用。其中,假设①是基于负荷分解领域中电器识别的研究成果。如文献[20]的负荷分解算法,无须已知用户拥有的电器设备数目、种类等信息,可以从负荷采样数据中抽取特征并与市面上常见的负荷设备特征库比较,分析出用户家中拥有的电器数量、种类等情况。而本文主要是基于电器识别的研究结果,研究EOI。假设②所需数据可以利用K-means聚类[21]等方法对市面上常见品牌、型号的电器设备曲线进行训练,获取电器设备各非零稳定工作状态对应的有功功率值。
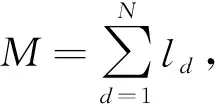
P=[P1,P2,…,PT]存储了总有功功率采样数据,单位为W。其中T为采样点个数。W=[W1,W2,…,WT]存储了总电量采样数据,单位为W·min。w=[w1,w2,…,wT-1]存储了相邻采样点间总负荷消耗的电能值,单位为W·min。其中,wi=Wi+1-Wi,i=1,2,…,T-1。
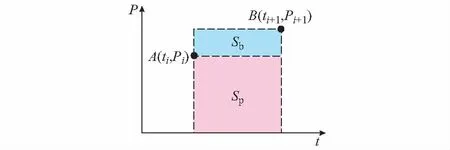
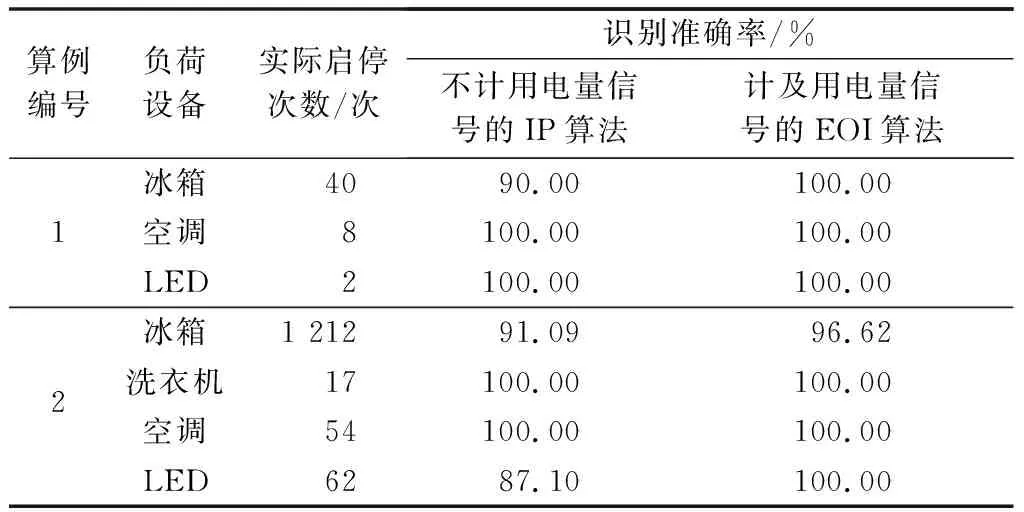
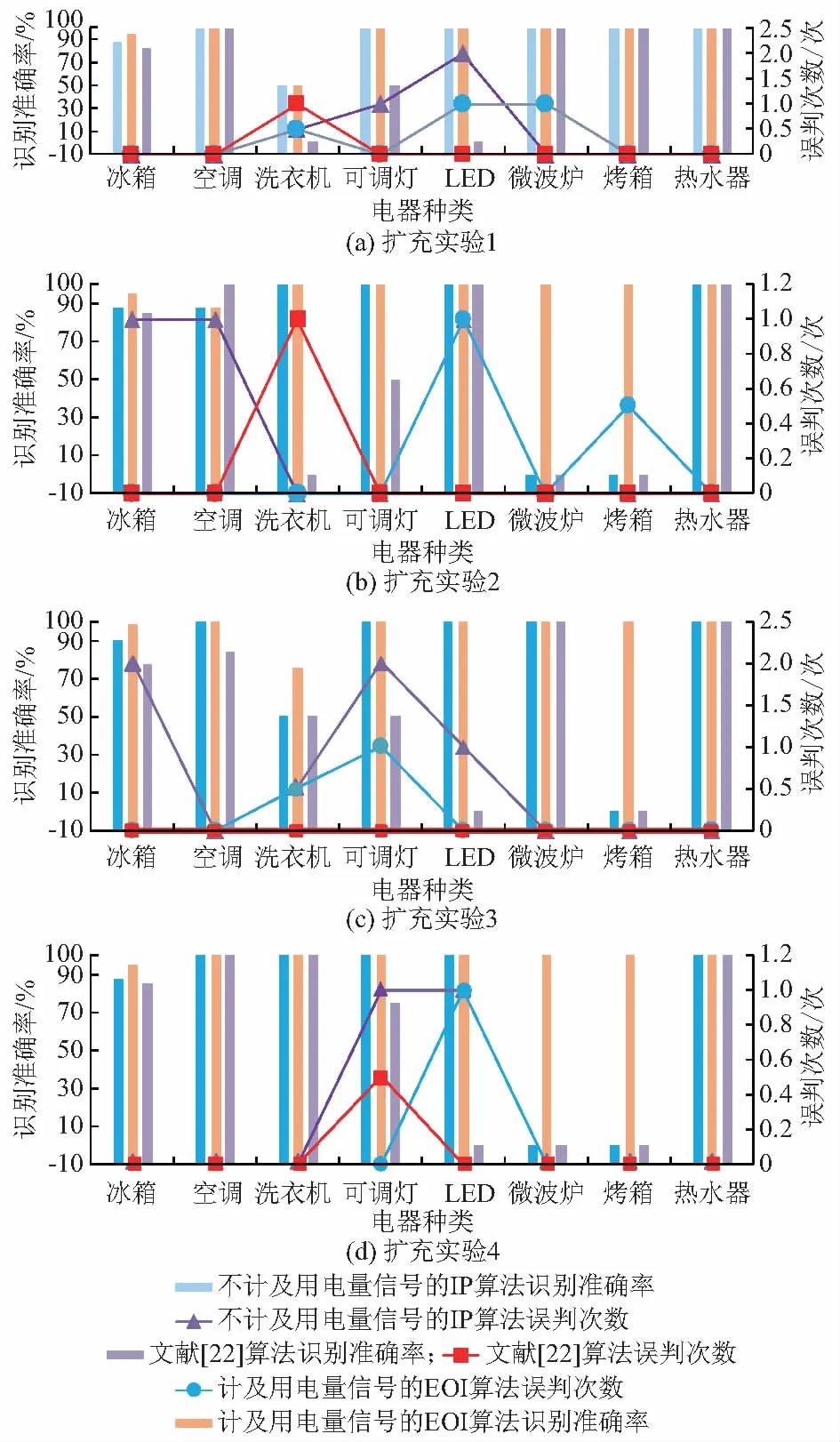
本节给出一种重构总有功曲线的方法,设Pi 假设1:家庭中负荷设备均已知,因此采样点间峰值(谷值)必然对应于负荷状态表中的某个值。 假设2:采样点间最多仅有一种设备发生了工作状态的改变。 假设3:当出现多个候选解时,本文选取与A和B点有功功率差值绝对值最小的为C点纵坐标值。 由假设2可知,A和B点间最多仅有一个峰值(谷值)。由假设1可知: |PC-Pi|=ΔP=|rs-Pi| s=1,2,…,M;i=1,2,…,T (1) 式中:PC为C点有功功率值;Pi为第i个采样点有功功率值;rs为负荷状态表中第s个非零稳定工作状态对应的有功功率值。且A,B,C点确定的曲线是方波,因而,A,B,C确定的曲线共有三种情况,具体如图2所示。 图2 重构后的有功功率曲线示意图Fig.2 Schematic diagram of reconstructed total active power curve 情况1:0≤wi 情况2:wi>Pi+1H。同理,若PC≤Pi+1,则SABC 情况3:PiH≤wi≤Pi+1H。观察图2可得,若PC 由假设3可知,此时A,B,C构成的曲线应如图2(c)所示。算法具体流程如下。 步骤1:计算向量r中任意两元素差值的绝对值。将计算所得结果按照升序排列。将结果存入向量E中。如果存在大小相同元素,仅保留其中一个。记E中的元素为Ej(j=1,2,…,L),其中L为常数。初始化i=1。 步骤2:初始化j=1。计算图3中点区域面积Sp=PiH,划线区域面积Sb=(Pi+1-Pi)H,本文中H=10 min。若wi 图3 步骤2示意图Fig.3 Schematic diagram of step 2 步骤3:取PC=Pi-Ej,若PC<0,PC=0。tC=ti→ti+1。计算A,B,C与横轴围成的面积S=PCΔt+Pi+1(H-Δt),其中Δt=tC-ti。 若|S-wi|<ε,C点坐标确定,按图2(a)所示将A,B,C相连,转去执行步骤6。否则,j=j+1,若j≤L,继续执行步骤3;若j>L,则该问题无解。其中,ε为允许的误差值。 步骤4:取PC=Pi+Ej,若PC>Pmax,PC=Pmax。其中,Pmax=maxPi,其中i=1,2,…,T,tC=ti→ti+1。计算A,B,C与横轴围成的面积S=PiΔt+Pi+1(H-Δt),其中t=tC-ti。 若|S-wi|<ε,C点坐标确定,按照图2(b)所示将三点相连,转去执行步骤6。否则,j=j+1。若j≤L,继续执行步骤4;若j>L,则该问题无解。 步骤5:PC=Pi+1,tC=ti→ti+1。计算A,B,C与横轴围成的面积S=PiΔt+Pi+1(H-Δt),其中t=tC-ti。 若|S-wi|<ε,C点坐标确定,按照图2(c)所示将三点相连,转去执行步骤6。 步骤6:i=i+1,若i 本文对完成重构后的总负荷有功曲线进行抽样,抽样间隔H′=1 min。则抽样得到的总功率时间序列P′=[P1′,P2′,…,PT′′],T′为总抽样点个数。 由于家庭中所有负荷设备已知,因此EOI问题可描述为:在第k(k=1,2,…,T′)个抽样点,对于包含N个电器设备的负荷对象,已知各设备状态对应的有功功率及总负荷有功功率,求取使得设备组合总功率与总有功功率偏差最小的最优组合。 3.1.1目标函数 该问题是一个优化问题,其目标是找到在第k个抽样点哪个设备状态处于开启状态,若记0-1决策变量bk(s)存储第k个抽样点,第s(s=1,2,…,M)种非零稳定工作状态的状态信息,bk(s)=1表示第k个抽样点该工作状态存在,否则该工作状态不存在。则该问题目标函数如式(2)所示[10]。 (2) 给定长时间负荷曲线(如日负荷有功曲线)后,可以预先将其分割成由单设备或者多设备同时运行的多个负荷子序列[14]。由于实际生活中各电器设备开关之间相对独立,各负荷子序列之间相关性较低,因此本文直接对各负荷子序列分别进行负荷分解,优化过程中不计子序列之间的相互影响。 3.1.2先验知识确定约束条件 本文所用先验知识主要有:①每种电器设备在第k个抽样点,最多仅有一个非零稳定工作状态;②通常,电器设备开启后至少运行一个周期;③人类用电具有规律性。如在01:00—04:00,家庭中诸如洗衣机负荷设备通常处于关闭状态。 通常,生活中违背先验知识2和3的情形是很少发生的,因而本文认为在做初步研究时此类情形可忽略不计。向量r中的元素按照附录A图A2所示方式进行排列,则第d台设备负荷状态集应为{rl1+l2+…+ld-1+1,…,rl1+l2+…+ld-1+ld}。 因此,引入记号qd=l1+l2+…+ld-1。为使该记号不失一般性,令l0=0。则第d台设备负荷状态集可表达为{rqd+1,…,rqd+ld}。 由先验知识1确定通用的约束条件:在任意第k个抽样点,第d台设备最多仅有一个非零稳定工作状态。该约束条件如式(3)所示: (3) 式中:d=1,2,…,N;j=1,2,…,Ttotal。 (4) 由先验知识2可得约束条件如式(5)所示。 (5) 由于本文的优化是逐时刻优化,因此式(5)表示的与前后时间相关的约束条件难以直接加入本文优化模型中求解。因此,在对3.1节建立的优化模型进行求解时,本文先对式(5)表示的约束条件进行松弛,对优化模型进行求解。再对求得的模型解进行事后校验,并根据校验结果对不满足式(5)的部分时段优化模型进行修正。 1)对式(5)表示的约束条件进行松弛 根据式(5),若式(6)成立,则在第j个负荷子序列中,第d台设备一定处于零工作状态。此时该约束条件如式(7)所示。 (6) (7) 对上述模型进行求解时,本文利用文献[10]方法,将模型转化为混合IP问题,在MATLAB中建立了相应的优化模型,然后调用CPLEX混合IP算法进行求解。 2)模型解事后校验 对模型解进行遍历,若模型解中第d台设备运行时间小于其正常运行周期,则该解违背式(5),应当被舍弃。 通过对大量错误解的分析,本文发现在该情况下,第d台设备实际处于关闭状态,而此时处于开启状态的某个设备实际上在暂态过程中。 本文设置决策变量Xs(s=1,2,…,M)表示第s种工作状态在暂态过程中实际对应的有功功率值。此时,事后校验部分的目标函数如式(8)所示。 (8) 式中:k=1,2,…,T′;j=1,2,…,Ttotal。 此时约束条件在式(4)和式(7)基础上,再加入式(9)。 (9) 对上述模型进行求解时,本文利用文献[10]方法,将模型转化为混合IP问题,在MATLAB中建立了相应的优化模型,然后调用CPLEX混合IP算法进行求解。 本节首先选取了家庭中最常使用的4种电器设备:冰箱、洗衣机、空调(制冷)、LED灯。其中,冰箱具有2个稳定运行状态,洗衣机具有4个稳定运行状态。 根据家庭用户日常使用习惯构建了典型日日负荷有功曲线以及月度负荷有功曲线。为验证本文算法的有效性,本节分别用不计及用电量信号的IP算法和本文所提的计及用电量信号的EOI算法对上述数据进行数值模拟,数值模拟中比较了两种算法对电器设备启停判断的结果。 接着,为进一步验证本文算法对于实际应用中的复杂场景同样具有参考借鉴意义,本文增加了负荷种类和数量,进行了扩充实验。实验中,本文新增了微波炉、烤箱、热水器以及具有两个运行状态的灯,此外,本文为冰箱新增了一个除霜的运行状态,并更换了一个功率更大的LED灯。其中,微波炉、烤箱、热水器以及除霜状态的冰箱曲线选自国外公开数据集REDD[10],本文模拟用户日常使用习惯操作设备,记录下各设备开关时刻,记录两周。并将各电器设备曲线按照记录下来的时刻进行叠加。本文从中选取了4组典型场景。此外,本文按照文献[22]算法对扩充实验中的场景进行了实验。本文在4.2节中对比分析了文献[22]以及本文算法在相对复杂场景下对电器设备启停判断的结果。 基础实验中选取的冰箱、空调(制冷)、LED灯、洗衣机4种电器设备的有功功率曲线见附录B图B1至图B4。负荷状态表如附录C表C1所示。 1)算例1:典型日求解结果 该场景中包含有冰箱、空调(制冷)以及LED负荷。该场景下冰箱保持持续运行。本文设定07:00—08:00和18:15—19:15冰箱压缩机频繁启停,即停止几秒后重新启动,模拟家庭中做饭时打开冰箱而导致其运行周期改变的现象。白天家中不开启LED负荷。12:00—15:00启动空调负荷,模拟夏季午休时家中开启空调的情形。该场景实际日负荷曲线详见附录B图B5。 表1中算例1部分给出了计及用电量信号的IP算法和本文算法对各负荷设备1日启停次数判断结果,并与实际情况进行了对比。 表1 算例1和算例2负荷启停次数识别准确率Table 1 Load on/off identification accuracies in case 1 and 2 表1算例1部分显示,本文算法对冰箱启停判断准确率提升了10%。原因在于:冰箱压缩机频繁启停时,其启停动作在采样间隔内,不计用电量信号的IP算法仅依据采样点处有功功率值无法检测到该过程,从而发生了漏判。 当实际启停时刻是采样间隔的倍数时,不计用电量信号的IP算法判断相对精确。但若负荷设备在采样间隔内动作时,不计及用电量信号的IP算法无法及时检测到这一动作。而本文提出的算法,考虑了用电量信息,可以在一定程度上刻画出采样间隔内实际有功曲线走势,从而较不计及用电量信号的IP算法更有效。 同时,本文还利用两种算法对空调(制冷)、LED等启停时刻进行判断,并与实际启停情况进行了对比。这里重点考察了判断误差较大(判断时刻与实际时刻误差超过2 min)情况的占比。在不计用电量信号的IP算法的结果中,这一比例为60%,而本文算法仅有25%。具体启停时刻识别结果详见附录C表C2。 2)算例2:月度求解结果 在算例2中,本文先对比了两种算法对各负荷设备一个月中启停次数判断结果,然后随机抽取一个月中的2 d,分别利用两种算法对该日设备启停时刻进行判断。 该场景中包含冰箱、洗衣机、LED以及空调(制冷)负荷,冰箱保持持续运行,早晚会开启LED负荷。部分时段存在空调(制冷)、洗衣机负荷。月负荷曲线详见附录B图B6。表1算例2部分给出了利用不计用电量信号的IP算法和本文算法对各负荷设备月启停次数识别准确率。结果显示,随着负荷启停次数的增加,两种算法对负荷启停识别的准确度均有所下降,但本文计及用电量信号可以估计采样点间有功波形走势,因而本文算法相较于不计用电量信号的IP算法更接近实际。 接下来,本文中在月度数据中随机抽取了2 d,比较两种算法对设备启停时刻判断情况。 1)算例2:时段1(第4日) 该时段下,LED、洗衣机负荷在采样间隔内启停。负荷有功曲线详见附录B图B7。本文统计两种算法对LED、洗衣机启停时刻结果与实际值相差超过2 min的比例,在不计用电量信号的IP算法识别结果中,这一比例为66.67%,而本文算法为0%。具体启停时刻识别结果详见附录C表C3。 2)算例2:时段2(第11日) 该时段中包含4种负荷设备。该时段下,空调启停两次,且存在多种负荷同时投切和运行。负荷有功曲线详见附录B图B8。 本文统计两种算法对LED、洗衣机启停时刻结果与实际值相差超过2 min的比例,在不计用电量信号的IP算法识别结果中,这一比例为50%,而本文算法为20%。具体启停时刻识别结果详见附录C表C4。 本文所提算法准确率较场景1有所降低,原因 在于该场景下有多种负荷同时投切和运行,本文重构的总有功曲线与实际曲线间存在误差,影响了第二阶段负荷分解的准确率。但本文方法在本算例中对设备启停时刻识别准确率同样较高。 总体而言,由于本文所提算法考虑了采样点间用电量信息,重构了总有功曲线,当负荷设备的动作发生在采样间隔内时,本文所提算法能够复原这一过程,从而较不计及用电量信号的IP算法更有效。 在扩充实验中,本文选取了家庭中8种电器设备:冰箱、洗衣机、空调(制冷)、烤箱、微波炉、热水器、大功率LED灯以及可调光的灯负荷。冰箱新增了一个除霜状态。烤箱、微波炉、热水器、冰箱除霜状态的有功功率曲线见附录B图B9至图B12。其他电器波形和基础实验中所述类似,本文这里不再赘述。选取的8种电器设备的负荷状态表如附录C表C5所示。 1)扩充实验1 该场景下夜间家中开了灯,以方便起夜,没有使用烤箱和空调。微波炉在07:55开启,持续5 min,采样点可以捕捉到其启停。负荷有功曲线详见附录B图B13。 图4(a)至(d)中柱形图分别给出了扩充实验1至4中,不计用电量信号的IP算法、本文算法以及文献[22]算法对电器启停次数识别准确率;折线图显示的是三种算法对电器启停发生误判的情况。需要说明的是,为了在柱形图中显示识别结果为零的数据,本节将图4中的纵坐标值设置从负数开始。 文献[22]算法进行负荷辨识时,分别将功率值以及运行时间与特征库中的特征进行匹配,若匹配不成功则认为该电器设备是未知设备。由图4(a)可见,该算法对已知电器设备启停的平均误判次数最少。但在10 min级别采样间隔下,采样得到的电器设备有功功率曲线会存在不同程度的失真,尤其是随机性较强,主要受人类活动影响的负荷(如可调灯等)以及波动较大的负荷(如洗衣机负荷),其运行时间或功率值与特征库中的差别较大,易被误认为是未知设备,引起漏判。该方法对洗衣机、可调灯和LED负荷的识别率均不高。不计用电量信号的IP算法由于不对失真信号做整体上的分析,加上该场景相对简单,没有大量电器设备同时运行,反而比文献[22]算法取得了较好的启停识别准确率。本文算法考虑用电量信号,可以估计负荷有功功率曲线走势,一定程度上还原设备运行特征,因而在三种算法中取得了最高的识别准确率。 图4 扩充实验1至4中三种算法对电器启停次数识别情况Fig.4 Identification of on/off times for electric appliance by three algorithms in expansion experiments 1 to 4 2)扩充实验2 该场景中,微波炉于08:31开启,运行时间为294 s;烤箱于14:33开启,运行时间为6 min。两种电器均在采样间隔内完成了启停动作。负荷有功曲线详见附录B图B14。 对比图4(a)和(b)可明显看出,在该场景中,三种算法对冰箱、空调、热水器的启停次数识别准确率相差不大,但是仅有本文算法可以检测到微波炉、烤箱的启停。仔细分析发现,由于微波炉、烤箱均在采样间隔内完成了启停动作,采样得到的负荷总有功功率数据中不包含这两种电器运行数据,因而其他两种算法不可能从采样数据中分析出微波炉和烤箱的启停信息。 但在微波炉和烤箱的运行段,用电量值有明显增加,本文算法基于此能估计出这两段中存在大功率负荷设备启停,在总有功功率曲线重构环节一定程度上还原出微波炉、烤箱的运行情况。该场景下用电量信号图详见附录A图A3。 3)扩充实验3 该场景波动性较强,一方面是在场景中增大了随机噪声,另一方面增加了波动性较强的负荷设备启停次数(本文指的是洗衣机负荷)。此外,该场景中微波炉在21:29开启,运行时间为5 min,烤箱则在14:33开启,运行时间为6 min。负荷有功曲线详见附录B图B15。三种算法对各电器设备启停次数识别准确率以及误判次数如图4(c)所示。 结合图4(a)至(c)可见,本文算法在波动性较强的环境下同样比较稳定,对各电器设备启停识别准确率与其他场景相当,且对各电器启停误判次数也没有出现明显上升,可以较好地应对实际中存在的一些波动性较大的场景。 4)扩充实验4 该场景与扩充实验2的类似,微波炉、烤箱均在采样间隔内完成了启停动作。但该场景多电器设备同时运行的时刻较少,电器启停识别整体上难度不大。负荷有功曲线详见附录B图B16。图4(d)中三种算法对电器启停次数识别准确率同样验证了这一点。除微波炉和烤箱外,对电器启停次数识别准确率均超过了91%,但三种算法中仍然只有本文算法可以检测到在采样间隔内启停的负荷设备。这在实际生活中是相当常见的场景,因此本文算法对于实际应用具有参考借鉴的意义。 扩充实验中,三种算法对电器设备启停次数识别整体平均准确率分别为79.33%,95.14%和58.95%。三种算法对扩充实验1至4不同场景下的识别平均准确率情况详见附录C表C6。 综上分析可见,在4种不同场景下,本文算法对各电器设备识别准确率比较稳定,启停次数识别整体平均准确率在95%以上。而当场景中包含有在采样间隔内完成启停动作的电器设备时,与其他两种算法相比,本文算法优势显著。 本节将讨论本文的算法的复杂度和运行效率。本文算法在I7-6700处理器,8 GB内存,Windows下的MATLAB 2012b平台上运行。 重构有功功率曲线的算法代码平均执行次数为[(M(M-1)/2+0)/2+1](T-1),整体时间复杂度为O(M2T)。 优化模型求解的算法受每次模型的具体情况影响,通过多次试验可以看出优化模型整体求解时间以及事后校验部分求解时间。具体而言,扩充实验1至4优化模型平均求解时间为316.505 s,事后校验部分平均运行时间为95.93 s。各场景的时间详见附录C表C7。事后校验部分每个时刻简化过的0-1变量数平均为19,需要重新求解的时刻数平均为12。各场景下0-1变量数及需要重新求解的时刻数详见附录C表C8。 此外,本文还对本文算法适用的采样间隔范围进行了测试。需要说明的是,本文算法适用的采样间隔范围与用户家中电器设备运行特性有关,本文结果代表的是在扩充实验中4组场景下进行测试的结果。本文中定义平均误差率(average error,AVE)来衡量曲线与实际曲线逼近程度。记实际曲线上点为Pi(i=1,2,…,K,K为实际曲线数据个数),待评估的曲线上点为Pi′(i=1,2,…,K),则平均误差率AVE计算公式如式(10)所示。 (10) 测试结果显示,当采样间隔在4 min以下时,总有功功率采样曲线与实际曲线的AVE值较小,不需要进行总有功功率曲线重构。而随着采样间隔的增大,重构曲线与实际曲线的AVE值总体随之上升。当采样间隔大于13 min时,AVE最大值已经超过28%。因此,本文算法适合于采样间隔在4~13 min的情形。测试结果详见附录A图A4至图A5。 本文利用用电量信号重构了有功功率信号,从而扩充了基于10 min级稀疏采样下的超离散有功功率信号的信息量。数值模拟的结果表明,利用用电量信号来扩充超离散负荷采样数据信息量的方法是可行的。本文提出的算法具有一定普适性,在不同场景下对于电器启停次数、启停时刻等均有较好的识别准确率,且能够在一定程度上复原负荷在采样间隔内的动作,从而较不计用电量信号的算法更有效。目前本文算法仅对电器启停情况进行判断,下一步将考虑如何实现对电器种类的识别。此外,如何充分利用功率波形特点等事前先验知识进一步逼近实际有功功率曲线是需要进一步研究的问题。 本文受到国家自然科学基金(51577031)和中国电力科学研究院有限公司自筹项目(DZ83-17-007)“快速响应负荷动态仿真模拟技术研究及开发”资助,特此感谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 吴烁民(1993—),男,硕士研究生,主要研究方向:电力调度、智能用电。E-mail: wushuomin2006@163.com 张凯锋(1977—),男,通信作者,博士,教授,博士生导师,主要研究方向:电力系统调度与控制、电力市场。E-mail: kaifengzhang@seu.edu.cn 王 颖(1989—),女,博士,讲师,主要研究方向:电力调度。E-mail: wangyingrice@126.com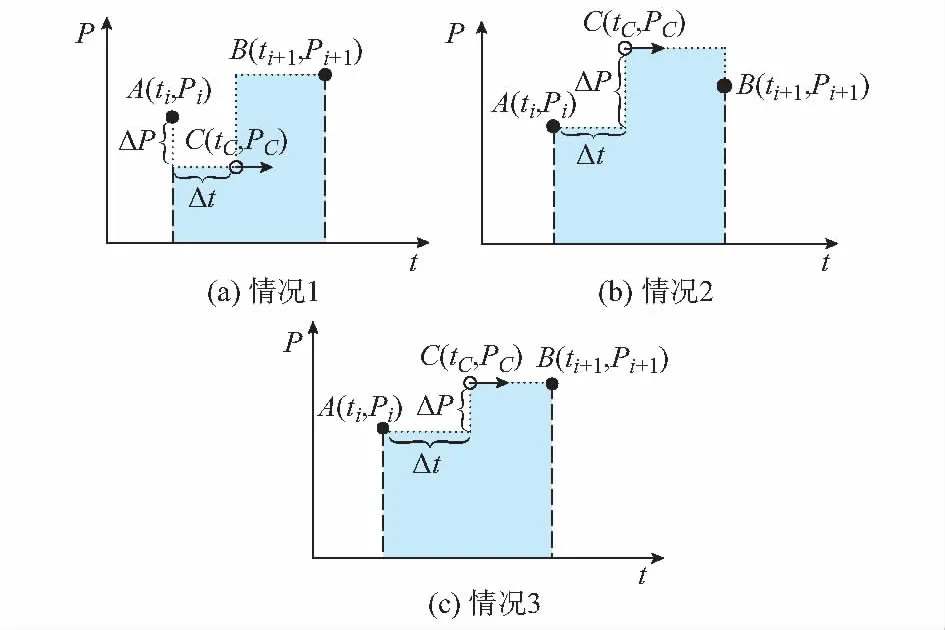
3 计及用电量信号EOI模型
3.1 优化模型建立

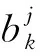
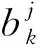
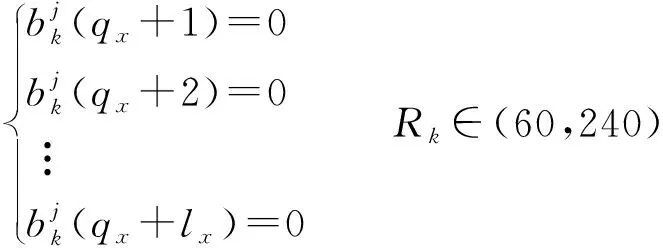
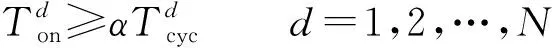
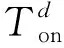
3.2 优化模型求解
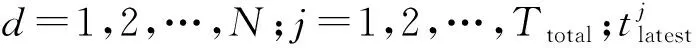

4 仿真与分析
4.1 基础实验
4.2 扩充实验
4.3 算法复杂度与运行效率
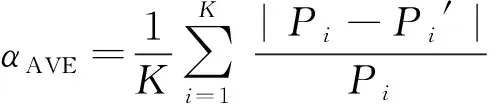
5 结语

