基波—谐波双通路并行感应耦合电能传输系统的电磁耦合机构

夏晨阳, 马 念, 陈 锐, 郑 凯, 任思源, 陈 俊

(1. 江苏省煤矿电气与自动化工程实验室(中国矿业大学), 江苏省徐州市 221116; 2. 南京南瑞继保电气有限公司, 江苏省南京市 211102)

0 引言

社会的快速发展对实现能源的高效传输及利用提出了更高的要求,如何实现电能高效、方便、安全的传输一直是学者们所关注的重点。无线电能传输(wireless power transfer,WPT)模式相比于以导线为媒介的传统有线电能传输模式,具有不易磨损、无接触火花、易维护、供电灵活等传统电能传输无可比拟的优点[1-2]。基于电磁感应原理的无线电能传输技术,即感应耦合电能传输(inductively coupled power transfer,ICPT)技术以其功率传输容量大、效率高等特点,在医疗设备[3-5]、手机[6]、家用电器[7]、电动汽车充电[8-10]等领域得到了广泛关注与研究。

ICPT系统在工作过程中,通常需要根据负载所需电压不同,对系统的输出电压进行控制[11],较为典型的方法有:①逆变器前或副边拾取侧之后加入DC-DC变换环节[12];②对高频逆变器进行移相控制[13];③加入辅助线圈,通过辅助线圈短路产生的磁通抵消主磁通[14]。上述方法虽然均可实现对系统输出电压进行调节,但依然存在相应的不足:方式①由于功率变换环节过多导致系统传输效率降低;方式②存在逆变器移相角不能过大的问题;方式③则存在控制精度低,系统损耗增大,系统传输效率降低等问题。

基波—谐波双通路并行ICPT系统以其输出电压范围宽、电能传输效率高和电压调节精度高等优势,逐步得到开展和应用[15-16]。然而由于基波—谐波双通路并行ICPT系统中特定的4线圈电磁耦合机构,4个线圈之间存在6种耦合关系,使得系统设计与分析复杂。为降低系统设计、建模与分析的难度,通常只考虑两通道对应线圈之间的耦合系数而忽略通道间交叉耦合系数对系统的影响[15-16]。现有常用的电磁耦合机构例如圆形、方形[17-18]可以应用在基波—谐波双通路并行ICPT系统中,但必须将基波能量通路(fundamental energy path,FEP)与谐波能量通路(harmonic energy path,HEP)的电磁耦合机构之间隔开较远距离,虽然可以实现双通路交叉耦合系数减小,但是电磁耦合机构属于分离式设计,造成其体积过大,因此在实际中的应用价值较低。DDQ和BPP[19-20]电磁耦合机构在原副边正对时也可实现FEP与HEP解耦,但在原副边发生横向或纵向偏移时,FEP与HFP之间的交叉耦合依然存在。因此,迫切需要一种新型的电磁耦合机构来满足基波—谐波双通路并行ICPT系统的需要。

本文借鉴DD型线圈结构[17],并基于正交磁场交叉无耦合的设计思想提出并设计了一种可以应用在基波—谐波双通路并行ICPT系统中的双通路正交DD电磁耦合机构。首先,介绍了该电磁耦合机构的结构组成,接着分析了其实现FEP与HEP两通路电磁耦合机构的解耦机理,并对其结构参数进行了优化分析，给出了优化设计方案,之后对该电磁耦合机构的偏移特性进行了研究。最后,搭建了完整的系统实验平台验证该电磁耦合机构的可行性。

1 基波—谐波双通路并行ICPT系统

图1所示为基波—谐波双通路并行ICPT系统原理图,在高频逆变器的输出端分别建立并联工作的FEP和HEP,两通路经过整流滤波电路之后,共同为负载提供电能。其中FEP与HEP均采用LCCL-S补偿拓扑以实现系统恒压输出[21-22],Uin为输入直流电压,Rp1为Lp1的内阻,Rp2为Lp2的内阻,R为负载,C1为FEP输出滤波电容,Vo1为FEP的输出电压,C2为HEP输出滤波电容,Vo2为HEP的输出电压,C3为总输出滤波电容,Vo为负载电压。

图1 基波-谐波双通路并行ICPT系统原理图Fig.1 Schematic diagram of ICPT system with two-path parallel transmission of fundamental wave and harmonic wave

图1中蓝色部分表示该系统中的电磁耦合机构及其互感耦合关系,其中k1和k2为FEP和HEP的有效耦合系数,k3,k4,k5,k6为通道间的交叉耦合系数。交叉耦合系数的存在增加了系统设计、建模、分析的难度,为降低系统设计的难度,本文设计了一种可以应用在基波—谐波双通路并行ICPT系统中的双通路正交DD电磁耦合机构,可以使系统中只存在有效耦合系数,不存在交叉耦合系数。

2 双通路正交DD电磁耦合机构

2.1 结构组成

图2所示为本文提出的双通路正交DD电磁耦合机构,可以实现基波—谐波双通路并行ICPT系统中FEP与HEP之间的电磁解耦,其由完全相同的FEP(红色)的电磁耦合机构与HEP(蓝色)的电磁耦合机构正交叠放组成,FEP的原边发射端与副边拾取端分别放置在HEP的原边发射端与副边拾取端的上方,灰色部分为条状磁芯,FEP与HEP的原边发射端与副边拾取端均由DD线圈组成。

图2 双通路正交DD电磁耦合机构Fig.2 Two-path orthogonal DD electromagnetic coupler

图2中：线圈的长度为l1,线圈的宽度为W,两个矩形线圈之间的距离为S1,原边发射端与副边拾取端的距离为S,线圈采用直径为d的利兹线缠绕而成,线圈匝数为N;磁芯条的长度为l2,磁芯条的厚度为h,磁芯条的宽度为W1,相邻磁芯条之间的距离为S2,定义邻近两个磁芯条之间的距离S2与线圈内轮廓的长度(l1-2dN)的比值为c,其表明磁芯的分布均匀度大小,其中磁芯条的个数为N1。

由于该磁路机构具有高度的中心对称性,结合图1与图2,显然6种耦合系数存在如下关系:k1=k2,k3=k4,k5=k6,因此为分析该电磁耦合机构中的FEP与HEP两通路之间的耦合关系,只需要对k1,k3,k5进行分析即可。

2.2 解耦分析

从本质上来讲,对两个耦合线圈1和2,当线圈1通过电流i时,两线圈之间耦合系数大小k可以通过其磁通分布来反映,其耦合系数如下:

(1)

式中:Φ为线圈1在线圈2中产生的耦合磁通;i为线圈1中的电流;L1为线圈1的自感;L2为线圈2的自感。

因此,对图2中电磁耦合机构存在的耦合系数进行分析，可以通过其磁通分布来获得。

为进一步分析该电磁耦合机构的磁通分布特性,利用有限元仿真软件对图2所示的电磁耦合机构进行仿真,在FEP的原边发射端中均通入电流ip1,则FEP原边发射端产生的磁通分布如图3所示,其中ΦM为FEP原副边的耦合磁通,Φa,Φb,Φc,Φd均为漏磁通,为简化分析,在图3(b)中并未绘制出漏磁通Φc和Φd。

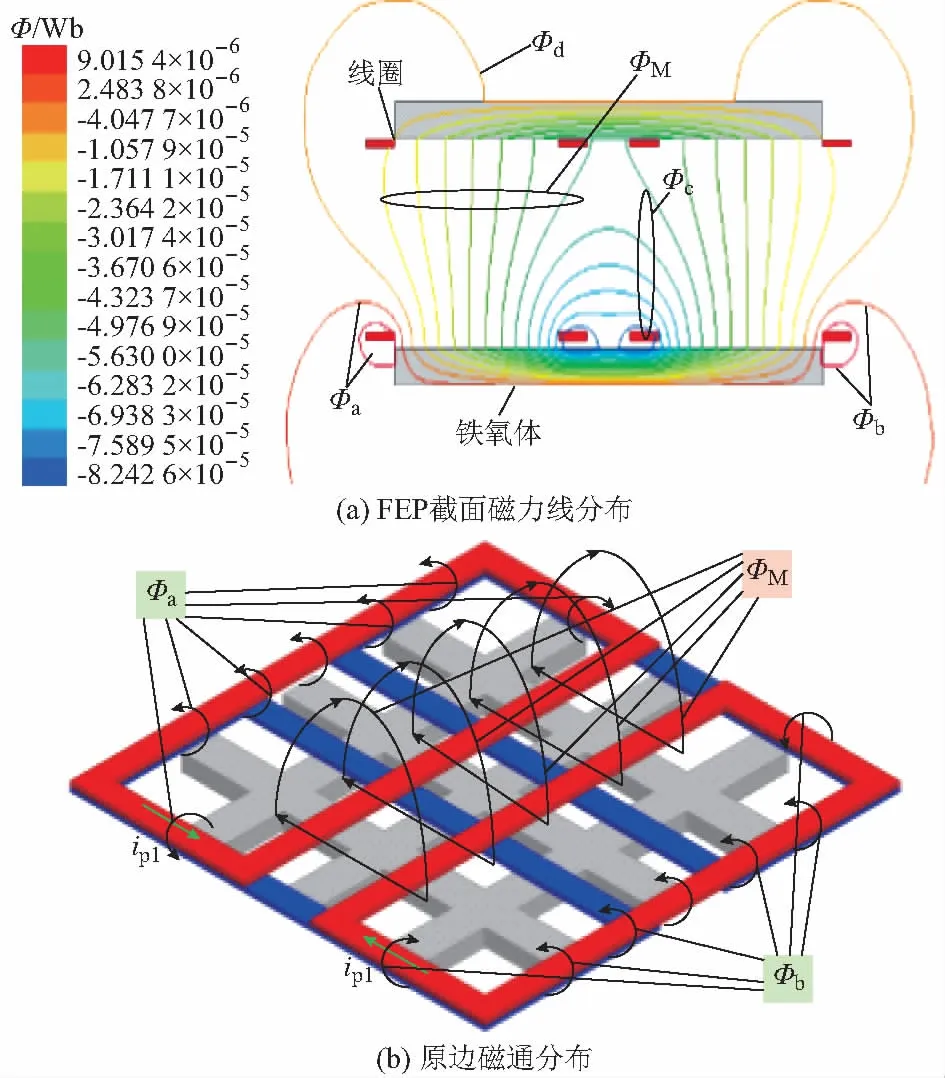
图3 双通路正交DD电磁耦合机构磁通分布Fig.3 Magnetic flux distribution of two-path orthogonal DD electromagnetic coupler

同时,为分析k1,k3,k5的大小,依据图3(a)所示的磁力线分布绘制出双通路正交DD电磁耦合机构的等效磁路模型如图4所示,则耦合系数有一种新的表达形式，如式(2)和式(3)所示。

(2)

(3)

式中:NIp1为磁动势;Rδ1,Rδ2,Rδ3为气隙磁阻;RFe1和RFe2为铁氧体磁阻,其相比于气隙磁阻很小,一般可以忽略不计;RL1和RL2均为漏磁阻;Ip1为电流ip1的有效值。

k1为有效耦合系数,k3为交叉耦合系数,其值大小均与磁动势、气隙磁阻、铁氧体磁阻、漏磁阻有关,结合图3(b)与图4可以得出,Φa=NIp1/RL1,Φb=NIp1/RL2,磁通Φa和Φb大小相等,方向相反,因此可知交叉耦合系数k3的值为零,同时HEP的副边拾取端与原边发射端在z轴方向上是平行放置的,因此交叉耦合系数k5的表达式与式(3)相似,其值也为零。

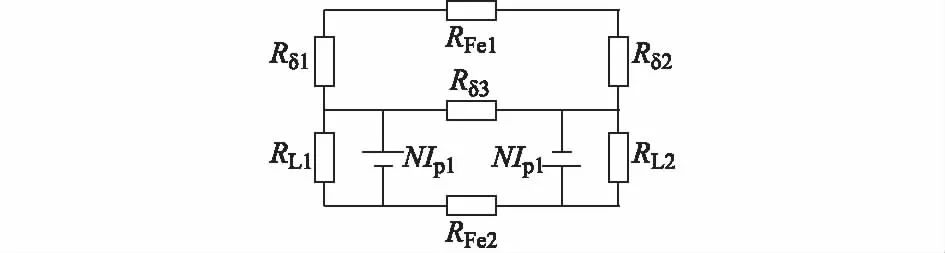
图4 电磁耦合机构FEP磁通分布等效磁路Fig.4 Equivalent magnetic circuit of magnetic flux distribution of FEP in electromagnetic coupler

因此,由理论分析可知,该双通路正交DD电磁耦合机构中交叉耦合系数均为0,可以达到基波—谐波双通路并行ICPT系统中FEP与HEP电磁解耦的目的。

3 仿真分析

3.1 优化分析

为使该电磁耦合机构中FEP与HEP的耦合系数均达到最优,利用有限元仿真软件Maxwell对该电磁耦合机构的关键结构参数(如图2所示)进行优化。

在该电磁耦合机构未使用磁芯的条件下,首先分析线圈的各个参数变化对电磁耦合机构耦合系数的影响,如附录A图A1所示。在优化过程中原边发射端与副边拾取端的间隙S为100 mm。

附录A图A1(a)和(b)表明电磁耦合机构的有效耦合系数随着矩形线圈长度与宽度的增加而增加,但是相比于长度的变化,线圈的宽度变化对电磁耦合机构的耦合系数有着较大的影响;图A1(c)是在DD线圈的长度l1为800 mm,W为400 mm的条件下研究电磁耦合机构的有效耦合系数随着DD线圈间距的变化情况,可以发现,电磁耦合机构的有效耦合系数随着DD线圈间距增加先增大后减小,间距在150 mm,即S1=(3/8)W时耦合系数最大,图A1(d)是在线圈的长度l1为950 mm,线圈的宽度W为400 mm,2个矩形线圈之间的距离S1为150 mm的条件下研究电磁耦合机构的有效耦合系数随着线圈的匝数N的变化情况,可以发现电磁耦合机构的有效耦合系数随着线圈匝数的增加而增加,几乎呈线性比例。

其次，分析磁芯条结构参数的变化对该电磁耦合机构有效耦合系数的影响,在优化过程中保持原副边间隙S为100 mm,线圈的长度l1为950 mm,线圈的宽度W为400 mm,两个矩形线圈之间的距离S1为150 mm,所用的磁芯是西安三联磁业科技有限公司生产的铁氧体,型号是sp3,附录A图A2所示是磁芯条的结构参数对电磁耦合机构耦合系数k的影响。

由附录A图A2可以看出,加入磁芯后电磁耦合机构的有效耦合系数明显提高,图A2(a)中电磁耦合机构的有效耦合系数随着磁芯条长度的增加先增加后减小,在磁芯条的长度达到870 mm时,同时此数值与矩形线圈的内轮廓的长度相等,电磁耦合机构的耦合系数达到最大值0.366;图A2(b)中磁芯条厚度增加到30 mm时,电磁耦合机构的有效耦合系数增加到最大值0.366,之后随着磁芯条的厚度再增加,电磁耦合机构的耦合系数不再增加而是维持在最大值;图A2(c)中使用总体积相同,长度、厚度相同,宽度不同的一系列磁芯条时,研究发现磁芯条的间距越小即磁芯分布越均匀,电磁耦合机构的耦合系数越高。

3.2 电磁耦合机构优化设计流程

由3.1节可知,通过优化分析可以使该电磁耦合机构具有最优的结构参数。在一个实际的基波—谐波双通路并行ICPT系统中,会给定电磁耦合机构的充电区域、原副边距离、互感及耦合系数大小作为电磁耦合机构设计的约束条件,因此按照3.1节的优化分析,可利用有限元仿真软件对该电磁耦合机构的结构参数进行优化设计,优化设计流程图如附录A图A3所示。

3.3 偏移研究

3.3.1偏移解耦分析

在实际应用场合中,电磁耦合机构原副边会不可避免地出现偏移情况,比如电动汽车静态和动态无线充电。因此,对该电磁耦合机构的偏移研究十分必要。

基于3.1节的优化分析,选取具有附录B表B1所示参数的电磁耦合机构,对其横向偏移与纵向特性进行研究,在该电磁耦合机构发生横向(x轴)和纵向(y轴)偏移时,6种耦合关系存在如下关系:k1≠k2,k3=k4,k5=k6。因此,该电磁耦合机构原副边发生偏移时,在图5中只绘制k1,k2,k3,k5的变化情况。

从图5可以看出,随着偏移距离的增加,该电磁耦合机构中交叉耦合系数k3和k5的值仍然维持在0附近,只是发生横向偏移时k1的下降速度快,而发生纵向偏移时k2的下降速度快,该电磁耦合机构依然可以实现FEP与HEP之间的电磁解耦。

3.3.2抗偏移度分析

依据3.3.1节的分析,虽然该电磁耦合机构原副边发生横向偏移或纵向偏移时,依然可以实现FEP与HEP之间的解耦,但是发生横向偏移或纵

图5 电磁耦合机构偏移对耦合系数k的影响Fig.5 Effect of electromagnetic coupler offset on the coupling coefficient k

向偏移时对有效耦合系数k1与k2的影响是不同的,因此横向偏移和纵向偏移会对系统输出电压有不同的影响,导致该电磁耦合机构具有不同的横向和纵向偏移特性。

结合文献[15]可知,基波—谐波双通路并行ICPT系统中FEP提供的输出电压与HEP提供的输出电压分别如式(4)和式(5)所示。

Vo1=ωaM1Ip1

(4)

Vo2=3ωaM2Ip2

(5)

在该电磁耦合机构正对时,令Vo1=εVo2,结合式(4)和式(5)可得系统输出电压如下:

Vo=Vo1+Vo2=3aωM2Ip2(ε+1)

(6)

同理可得在该电磁耦合机构发生横向或纵向偏移时系统的输出电压如下:

(7)

式中:M1′为电磁耦合机构偏移时Lp1与Ls1之间的互感;M2′为电磁耦合机构偏移时Lp2与Ls2之间的互感。

在发生偏移时,对系统输出电压做归一化处理,结合式(6)和式(7),可得:

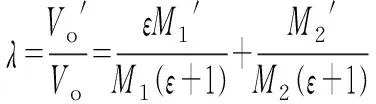
(8)

式中:λ为归一化电压。

附录A图A4是在电磁耦合机构原副边发生横向(x轴)和纵向(y轴)偏移的情况下,系统输出电压的归一化处理结果,其中ε值为3。从该图可以看出:在ε为3时,发生横向偏移时,系统的输出电压下降较为快速;发生纵向偏移时,系统的输出电压下降较为缓慢。同时,在满足系统输出电压在0～5%的范围波动时,其横向偏移度为7.05%,纵向偏移度为9.09%。

4 实验验证

为验证本文提出的双通路正交DD电磁耦合机构的可行性,依据文献[15]的设计方法,在不采用移相控制,FEP与HEP同时工作的条件下搭建了一个逆变器工作频率为30 kHz、输出功率为300 W的系统,系统中各个元件的参数如附录B表B2所示,同时依据3.2节的优化设计流程方案对所需的电磁耦合机构的结构参数进行设计,电磁耦合机构的结构参数如附录B表B3所示,依据表B2与表B3的参数搭建的实验平台如附录A图A5所示。

附录B表B4测得的是在原副边距离为100 mm的条件下,该电磁耦合机构的各个耦合系数的仿真结果与实验结果,从中可以看出,交叉耦合系数k3,k4,k5,k6的值均很小,为有效耦合系数k1和k2的1/148～1/370,可忽略不计,仿真结果与实验结果相差很小。

附录A图A6为实验平台采用的电磁耦合机构在原副边发生横向和纵向偏移时其耦合系数的实际变化情况。从该图可以看出,在该电磁耦合机构发生横向和纵向偏移时,交叉耦合系数依然为0,因此可以实现FEP与HEP之间的电磁解耦。

附录A图A7是实验平台系统中各关键点的电压与电流波形,从图A7(a)和(b)可以看出,FEP与HEP电路均略呈感性,可以实现逆变器软开关,减小开关损耗;从图A7(c)和(d)可以看出,FEP的选频特性较好,而HEP的选频特性效果不是太理想,是由于HEP中的FTH相较于FEP中的HTF较大(HTF表示FEP中的三次谐波电流与基波电流的比值,FTH表示HEP中的基波电流与三次谐波电流的比值),同时方波中基波含量较大,使得HEP中的基波分量不能完全滤除[15];从图A7(e)可以看出，FEP提供输出电压67.5 V,HEP提供输出电压19.8 V,则系统的总输出电压为87.3 V,传输功率为304.8 W,系统效率为90.48%。

附录A图A8为电磁耦合机构发生偏移时系统输出电压的变化情况,可以看出在该实验平台发生横向偏移或纵向偏移时,系统的输出电压均会出现下降的情况,若要保证输出电压在0～5%的范围内波动,则最大的横向偏移距离与纵向偏移距离分别为27.99 mm和36.17 mm,则本系统的横向偏移度为6.99%、纵向偏移度为9.04%。相比于横向偏移,该电磁耦合机构纵向偏移容忍度较好,可以较好地与3.3.2节的理论分析相印证。

5 结语

对于本文所提出的双通路正交DD电磁耦合机构,通过理论分析、优化研究,在该电磁耦合机构实现基波—谐波双通路并行ICPT系统FEP与HEP电磁解耦的同时,通过优化电磁耦合机构的结构参数可以使其有效耦合系数达到最优,在该电磁机构发生横向或纵向偏移的情况下依然可以实现电磁解耦,只是对系统的输出电压有不同的影响而且该电磁耦合机构具有较好的纵向偏移容忍度,本文搭建的300 W系统实验平台也表明该电磁耦合机构的可行性。由于本文电磁耦合机构中线圈采用手工绕制、磁芯采用小型的铁氧体拼凑而成,导致电磁耦合机构与理论仿真之间存在一定的误差。下一步的工作是针对某一特定场合的负载,例如电动汽车,在满足输出功率的条件下,设计一套具有高抗偏移容忍特性的基波—谐波双通路并行ICPT系统。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

夏晨阳(1982—),男,通信作者,博士,副教授,硕士生导师,主要研究方向:无线电能传输技术、自动控制技术、开关电源技术、电磁兼容等。E-mail： bluesky198210@163.com

马 念(1993—),男,硕士研究生,主要研究方向:无线电能传输技术及其应用。E-mail: 1597605432@qq.com

陈 锐(1991—),男,硕士研究生,主要研究方向:无线电能传输技术及其应用。E-mail: 578077169@qq.com