一种低单盘故障恢复开销的局部修复码

萧 枫，唐 聃，范 迪，白宁超

1.成都信息工程大学 软件工程学院，成都 610225

2.四川省计算机研究院，成都 610041

1 引言

近年来，随着信息技术的快速发展，世界上的数据量正不断增长，而存储系统的规模也日益增大，廉价存储设备的应用也逐渐变得广泛。而随着规模的增大、廉价磁盘数目的增多，存储系统中磁盘发生故障的概率也在上升，从而导致存储系统的稳定性所面临更加严峻的挑战。因此大多数存储系统都会为了保障数据的可靠存储而使用容错技术。

常用的容错技术有两种：副本技术和纠删码技术。副本技术是指通过复制原数据并存储其副本，来保障当发生任意小于副本数目的错误时，都可以通过备份的副本来保障数据的完整性和可靠性。副本技术的优点在于算法简单，易于实现，且恢复速度极快。而副本技术最大的缺点在于存储开销过大，需要许多的冗余存储才能够保证数据的可靠。而纠删码技术则是通过相应的算法来生成少量的冗余数据，并与原数据一起存储。当故障发生时，则通过对应的解码算法对于剩余数据和冗余数据进行运算得到原数据。纠删码技术解决了副本技术带来的冗余过多的问题，同时能够在一定程度上保证数据的完整性和可靠性，因此是目前存储系统中主流的容错策略。

在纠删码技术中，阵列纠删码由于基于异或计算，编译码速度快的特点而被广泛应用。典型的阵列码包括 EVENODD[1]、RDP[2]、STAR[3]、RTP[4]等等，而 RDP 码是存储系统中较为常用的一类容两错的阵列码。其原理主要是通过增加额外的两个冗余磁盘来保证数据的完整性，因此RDP能够在任意的两个数据磁盘发生故障后仍正确地恢复出原始数据。

对于RDP编码而言，其优点在于结构简单，编译码过程基于异或运算，因而速度很快。但是其主要缺点之一就是单盘故障恢复所需读取的数据过多，需要读取所有的剩余原数据。而在存储系统的故障失效情况中，单一磁盘故障的比例达到99.75%[5]，而纠删码高额的恢复读取开销会给数据中心原本就紧张的带宽资源[6]带来更大的压力。文献[7]则论述了降低单盘故障的恢复时间可以提高整个存储系统的稳定性。因此为减少读取开销，降低单盘故障恢复时间，提出一种新的RDP单盘故障恢复算法。考虑到传统RDP编码中单数据盘故障的恢复是基于单个校验盘，若增加一个只由部分数据盘计算得到的局部校验盘，能够使得当这些数据盘发生故障时，仅需要读取生成局部校验盘的数据盘就能够恢复，从而达到减少读取开销的目的。

2 RDP介绍

2.1 RDP编码过程

RDP（Row Diagonal Parity）的编码过程是基于一个规模为(p-1)×(p-1)的原数据阵列，其中 p为素数。假设阵列中每一列代表一个磁盘，而磁盘中存储的数据块为ai,j,i和 j分别表示元素的行列坐标，且坐标均从0开始计。

编码过程分为两步，第一步是计算水平冗余列。计算方法是将 p-1个数据列横向进行异或，其编码过程如式（1）所示：

第二步是计算对角冗余列。方法是将由p-1列原数据以及第一步生成的水平冗余列构成的规模为(p-1)×p的新阵列中行列坐标之和模 p结果相同的数据块进行异或构成对角冗余列。其编码过程如式（2）所示：

最终的编码过程如图1所示，最终得到一个包含两列冗余列的规模为(p-1)×(p+1)的阵列。

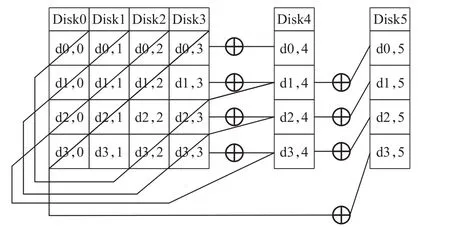
图1 水平冗余和对角线冗余计算过程

2.2 RDP单盘故障恢复过程

传统的RDP单盘故障恢复方法可以根据丢失的列位置分为数据列丢失和冗余列丢失两种类型。

数据列丢失的恢复过程为读取出其他全部的数据列的数据块以及水平冗余列的数据块进行异或运算，得到丢失的数据列。恢复所需要读取的数据盘如图2所示，其中“×”表示丢失的数据块，“○”表示恢复所需要读取的数据块。

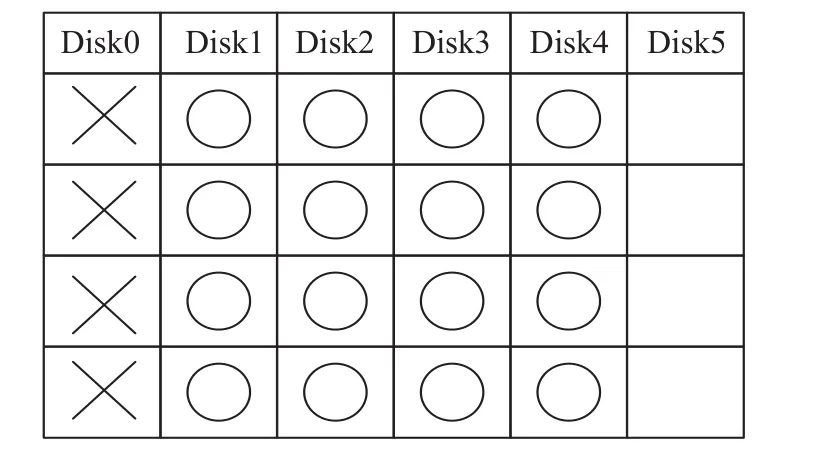
图2 单盘故障恢复所需读取的数据

由图2可知，当数据列发生故障时，需要读取的列数目为p-1，即原阵列中总共的数据列列数。

冗余列丢失的恢复过程同编码过程一致，即通过编码算法再次生成冗余列即可恢复。显然当冗余列发生故障时，需要读取的列数目依然为p-1。

因此对于传统的单盘故障恢复方法而言，无论是数据列丢失还是冗余列丢失，恢复过程所需要读取的列数量均为p-1个。

2.3 RDP相关研究

为了对RDP进行扩展，文献[8]提出在RDP基础上再增加一个冗余列，其计算过程是将斜率为-1的斜线上的数据块进行异或，构造出一种新的三容错RAID码。而文献[9]则同样提出在RDP基础上增加新的冗余列，其计算过程是将斜率为2的斜线上的数据块进行异或，得出了另一种新的三容错RAID码。

而为了降低单盘恢复开销，文献[10]提出，对于RDP编码，当某一个数据盘发生故障时，可以同时使用两个冗余列，即水平冗余与对角线冗余来进行恢复。由于使用不同方法恢复会产生重复读取的数据块，因此可通过缓存这些块来降低读取开销。该文献同时对于理论上的读取下限进行了推导和证明，发现最小的恢复开销是对于一半数据使用水平冗余进行恢复，对另一半数据使用对角线冗余进行恢复。最终计算得到该混合恢复算法理论上恢复开销的下限是总数据量的3/4，即能够节省25%的读取开销。

如图3所示，当Disk0失效时，对于前两个数据块通过水平冗余列来进行恢复，对于后两个数据块通过对角线冗余来进行恢复。其中“○”表示利用水平冗余所需要读取的数据块，而“□”表示利用对角线冗余所需要读取的数据块，而两者都有则表示重复的数据块。

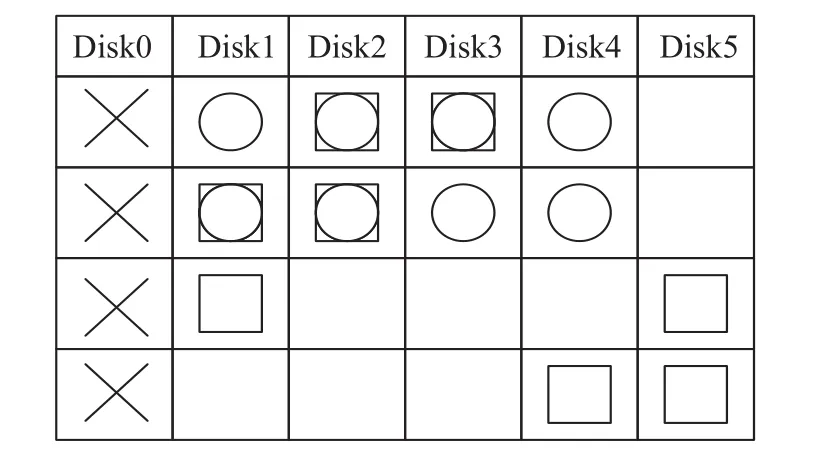
图3 混合恢复算法的单盘故障恢复读取开销

文献[11]则提出了一种针对RDP单盘故障恢复的不同方案。该方法通过将水平上的部分不参与对角冗余计算的数据块进行异或产生额外的冗余块，并使用产生的冗余块来代替原来的多个数据块，从而达到降低数据读取开销的目的。而针对于容三错的阵列码而言，文献[12]同样提出了混合使用三列冗余列来进行单盘故障恢复的方法。其具体方法是通过对于丢失的p-1数据元素选取p-1个合适的校验元素将其恢复，并平均使用3中校验元素，使得校验方程中需要的数据块尽可能多的重合，以此来达到降低数据读取量的目的。

然而混合恢复算法也带来了磁盘随机访问的问题，文献[13]在保证数据读取量最少的前提下，为RDP设计出一种新型的、支持连续读的单磁盘故障修复策略，最大程度上维持了磁盘访问的连续性，加快了单磁盘故障的修复效率。

3 局部修复RDP编码及相关性质

为了进一步地降低RDP码在单盘故障时的恢复读取开销，缩短恢复时间，本文构造了一种LRRDP码（Local Repairable RDP）。

3.1 编码过程

LRRDP码的编码过程如图4所示，相同形状的白色元素生成对应的黑色校验块。

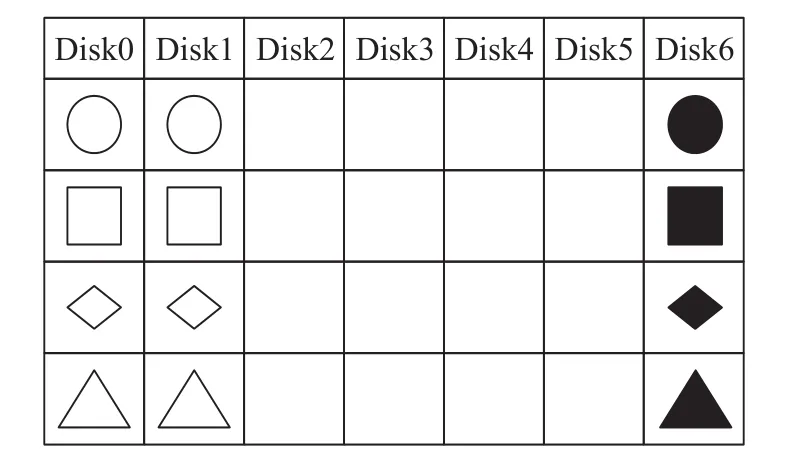
图4 LRRDP编码过程

3.2 编码开销

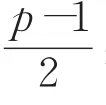
4 局部修复RDP解码

4.1 单盘故障

对于传统的RDP编码，修复单盘故障（非冗余列）的方式是通过读取剩余数据列以及水平冗余列进行异或来恢复。对于LRRDP，修复单盘故障分为4种情况。

4.1.1数据列丢失

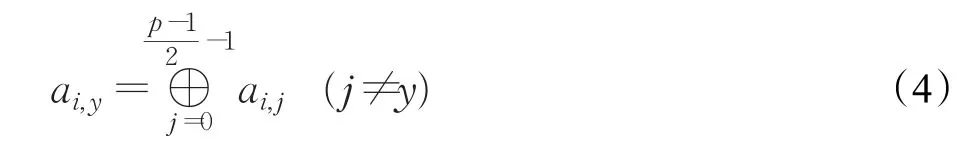
恢复所需的数据块如图5所示，“×”表示丢失的数据块，“○”表示恢复所需要读取的数据块。

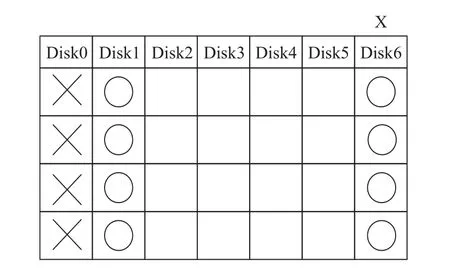
图5 丢失数据列在前半部分时所需读取数据

恢复所需的数据块如图6所示。

图6 丢失数据列在后半部分时所需读取数据

4.1.2 局部冗余列丢失

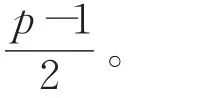
4.1.3 水平冗余列丢失

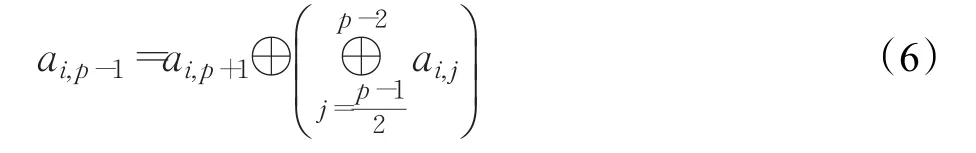
4.1.4对角冗余列丢失

对角冗余列丢失的恢复过程与编码过程相同，恢复的读取开销为 p。同样当 p不断增大时，这种故障在所有单盘故障中所占的比例将不断降低。

对于单盘故障恢复来说，假设每个盘发生故障的概率一致，则扩展后的RDP单盘故障恢复平均开销如式（7）所示：

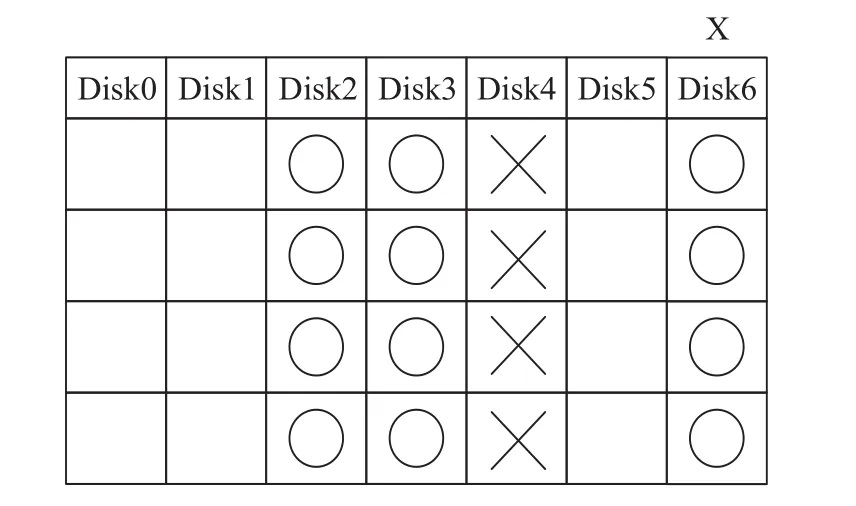
图7 水平冗余列丢失时所需读取数据

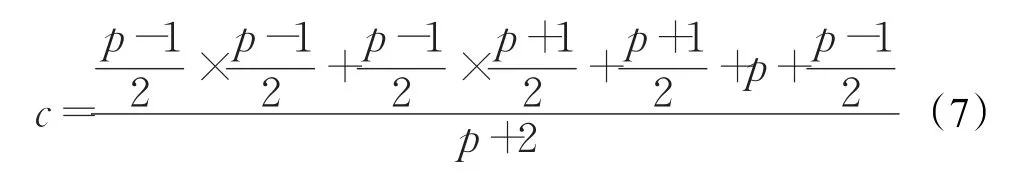
4.2 双盘故障

4.2.1丢失两列数据列

对于扩展后的RDP，丢失两个数据列的恢复过程与传统RDP的双盘故障恢复方法相同，数据的读取开销如式（8）所示：

4.2.2 丢失一列数据列和局部冗余列

设丢失的数据列为y，恢复过程为读取剩余数据列和水平冗余列进行异或恢复出丢失数据列，恢复公式如（9）所示：

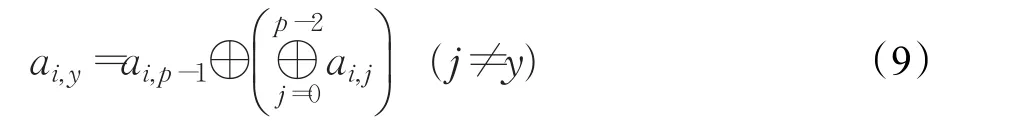
再通过编码方式恢复局部冗余列，恢复完毕。Disk1与局部冗余列列丢失时所需读取的数据块如图8所示。

图8 双盘故障恢复所需读取数据

由式（8）可知，故障恢复数据读取开销为 p-1列。

4.2.3丢失一列数据列和水平或对角线冗余列

恢复过程与传统RDP恢复方法一致，读取开销为p-1列。

4.2.4丢失两列冗余列

恢复过程与编码过程相同，显然，当丢失水平和对角冗余列时，读取开销为 p-1列。当丢失水平和局部冗余列时，读取开销也为p-1列。而当丢失对角和局部冗余列时，读取开销为p列。

综上，对于任意的双盘故障，LRRDP能够保证数据的完整性和可靠性。同时，LRRDP的双盘故障恢复读取开销与传统RDP保持基本一致。

4.3 三盘故障

LRRDP中的三个冗余列的计算可由式（10）～（12）表示：

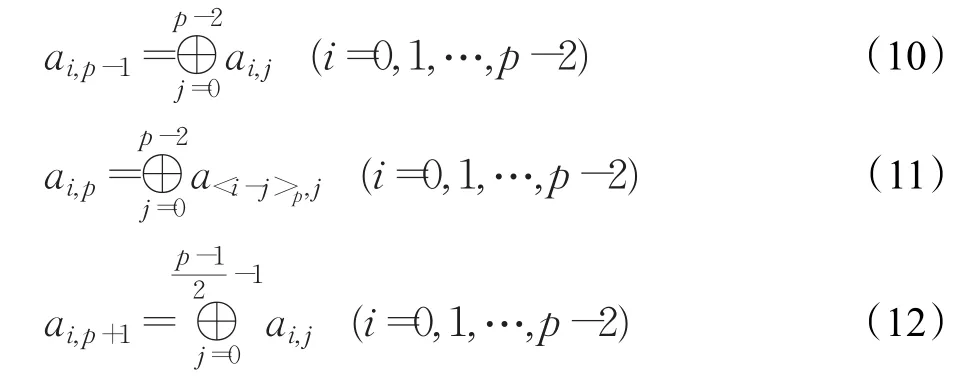
同时设每个磁盘发生故障的概率为γ。

在LRRDP中，三盘故障恢复的关键在于将三盘故障转换为传统的RDP双盘故障情况。对于传统的RDP双盘故障恢复过程，文献[2]中有具体描述，不再赘述。

4.3.1 丢失的三列均为数据列

当丢失的均为数据列时，按照三个数据列的位置分布可以分为三种情况。

这种情况不可恢复。

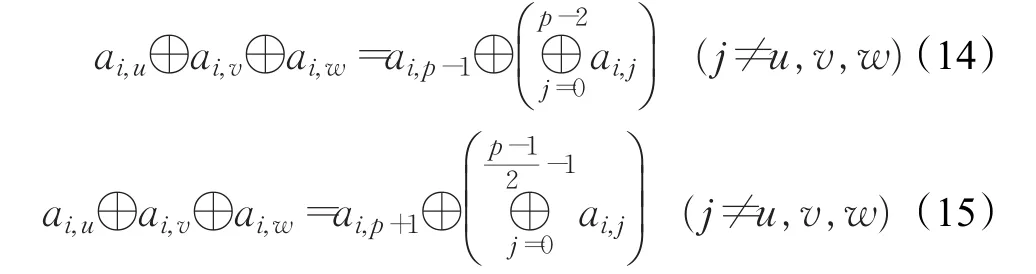
对式（14）经过变换后可得式（16）：

将式（16）代入式（15）得式（17）：

显然式（17）为恒等式，即ai,u、ai,v和ai,w有无穷多解，所以不可恢复。

恢复过程为通过局部冗余列恢复丢失列y，恢复公式如式（19）：

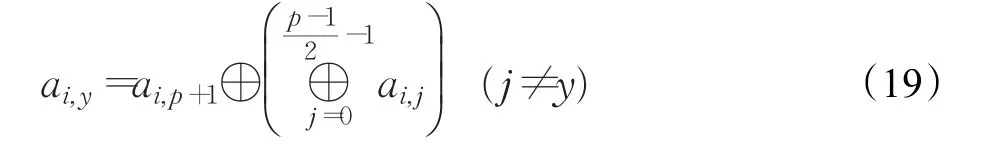
再通过传统RDP解码方法恢复剩余两个丢失列，恢复完毕。

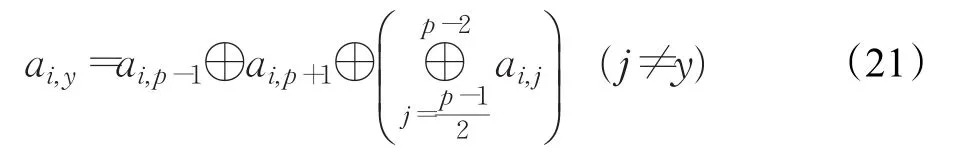
再通过传统RDP解码方法恢复剩余两个丢失列，恢复完毕。

4.3.2 丢失的两列为数据列，一列为冗余列

当丢失三个列，其中有两个是数据列，另外一个是冗余列，根据冗余列类型可分为三种情况。

第一种情况是局部冗余列丢失，发生的概率如式（22）：

恢复过程为通过传统RDP解码方法恢复丢失的两个数据列，之后通过编码方法重新生成局部冗余列。

第二种情况是水平冗余列丢失，根据丢失的两个列的位置可分为两类。

这种情况无法恢复。

再通过传统RDP解码方法恢复丢失的数据列和水平冗余列，恢复完毕。

第三种情况是对角冗余列丢失，根据丢失的数据列的分布情况也可以分为两类。

这种情况无法恢复。

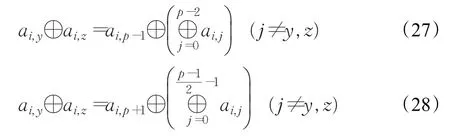
其中对式（27）经过变换后可得式（29）：

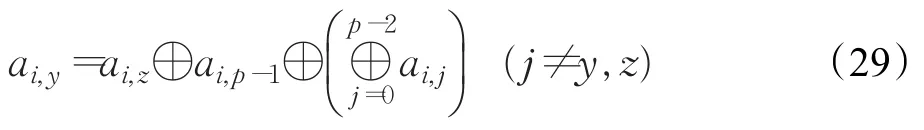
将式（29）代入式（28）得式（30）：

显然式（30）为恒等式，即 ai,y、ai,z有无穷多解，所以不可恢复。

4.3.3 丢失一个数据列，两个冗余列

根据剩余的冗余列类型可以分为两种情况。

第一种情况是剩余的冗余列是水平冗余列或对角冗余列，发生的概率如式（32）：

恢复过程为通过传统的RDP双盘恢复方式恢复两个丢失的数据列，再通过编码的方式重新生成局部冗余列，恢复完毕。

第二种情况是剩余的冗余列为局部冗余列，根据丢失的数据列位置可以分为两类。

恢复过程为利用局部冗余盘来将丢失的数据列恢复，恢复公式如式（25）所示。再通过编码方式恢复其他的冗余盘，恢复完毕。

这种情况无法恢复。

证明设丢失的数据列为y，显然，在构成局部冗余列的方程式（12）中，并不包含元素ai,y，因此不可恢复。

4.3.4 丢失三列冗余列

丢失的三列均为冗余列，发生的概率如式（35）：

恢复过程为通过编码再次生成三个冗余列。

由以上的讨论可得，不可恢复的情况概率之和如式（36）：

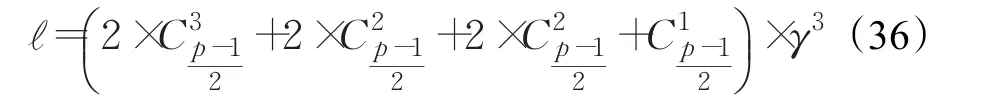
而出现三盘故障的概率如式（37）：

因此不可恢复的情况占所有三盘故障情况的比例如式（38）：

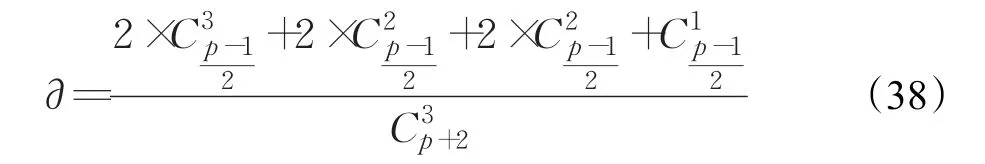
5 性能测试

本章通过在集群环境下测试比较RDP与LRRDP的单盘故障恢复性能。实验环境集群中的机器参数为：CPU Intel Core i7-3632、内存8 GB、磁盘500 GB、测试文件大小10 MB。

5.1 编码测试

图9给出了当确定文件块大小时，素数p取不同值时所需的编码时间。

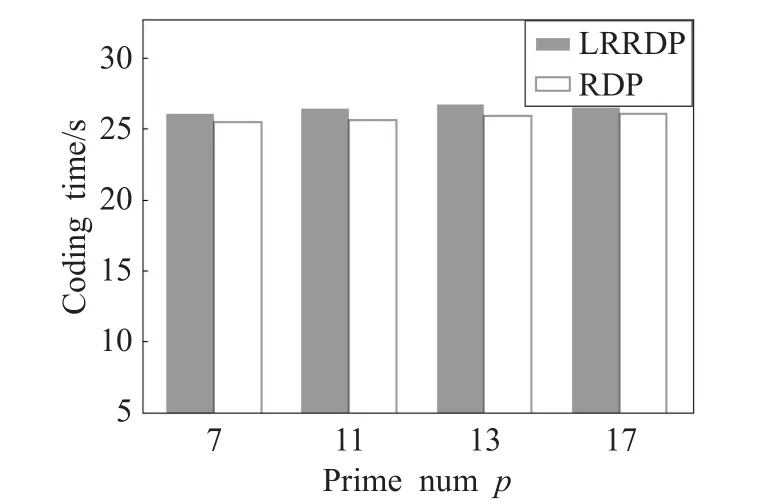
图9 编码时间比较

由图9可知，LRRDP编码时间仅比传统RDP编码时间略多。

5.2 单盘故障恢复测试

图10为 p取不同值时RDP与改进后的RDP的单盘故障恢复开销在理论上的对比。

图10 理论上单盘故障恢复读取开销对比

而图11则给出了实际测试过程中，单盘故障恢复时RDP和LRRDP所需要读取的文件块数的比较。

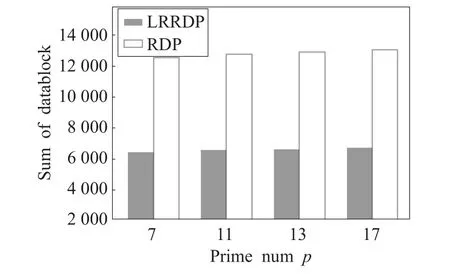
图11 单盘故障恢复读取开销对比

通过图11可知，LRRDP在单盘故障恢复中所需的数据块个数接近于RDP的50%。

图12给出了当确定素数 p时，块文件大小不同时的单盘故障恢复时间，而图13则给出了当素数 p取不同值时的单盘故障恢复时间。

图12 p不同时单盘故障恢复时间对比

图13 块大小不同时单盘故障恢复时间对比

通过测试结果可得，当 p取值增大，块文件大小增大时，单盘故障恢复读取开销降低的越多。当 p=17、块文件大小取5 000 Byte时，开销降低达到了45%。

5.3 双盘故障恢复测试

图14给出了当确定文件块大小时，素数 p取不同值时所需的双盘故障恢复时间。

图14 双盘故障恢复时间对比

5.4 三盘故障恢复测试

图15 给出了当发生10 000次三盘故障，素数 p取不同值时的不可恢复情况发生的次数。

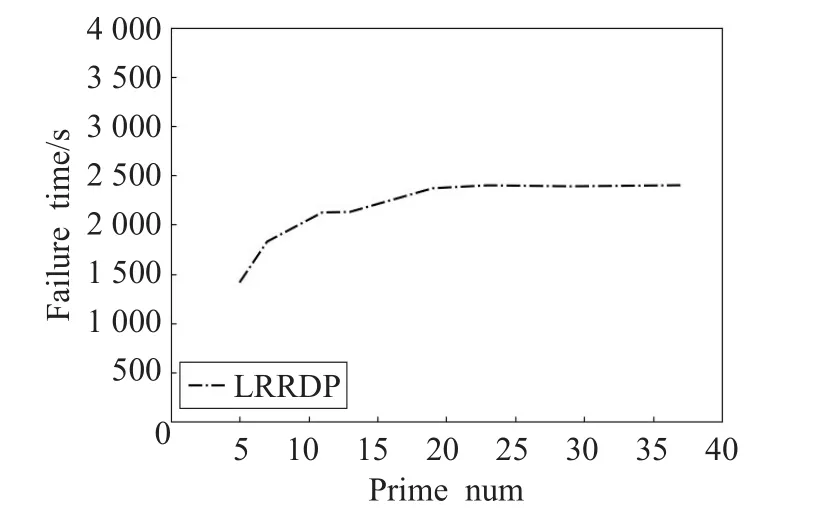
图15 不可恢复的三盘故障次数

由图15可知，当 p逐渐增大，不可恢复的次数逐渐稳定接近于2 500次，即三盘故障总次数的25%。

图16给出了当确定文件块大小时，素数 p取不同值时所需的三盘故障平均恢复时间。

图16 三盘故障平均恢复时间

6 结束语

本文针对RDP编码存在的单盘故障恢复读取开销比较大的问题，对其进行了改造。结合LRC对于RS码的改造，构造了一种局部修复码LRRDP。LRRDP码通过加入一列新的冗余列来减少单盘故障时的读取开销。实验结果显示LRRDP码可以有效降低单盘故障恢复的读取开销，同时可以恢复75%的三盘故障情况，能够提升海量数据存储系统的稳定性和可靠性。实际上，对于EVENODD、STAR以及RTP码等斜率码，都可以采用类似改进方法进行改造，相关证明和测试等工作还有待进一步完成。