基于采样点正交变换的改进CKF算法
赵 丽,薛建平
1.陕西国际商贸学院 商学院,陕西 咸阳 712046
2.空军工程大学 航空航天工程学院,西安 710038
1 引言
从统计学意义上讲,随机量的概率密度函数可以表征所有的统计信息。递归贝叶斯估计(Recursive Bayesian Estimation,RBE)综合利用了概率论中的贝叶斯准则以及随机量的Markov特性,为状态概率密度推演提供了一个最优的、精确的框架模型。但是,在对概率密度进行递归求解时RBE涉及多个多维积分,一般情况下无法求得其解析解。因此,虽然RBE在理论和形式上是“完美的”,但在实际应用中,需进行各种近似以求解出多维积分解析解。
递归贝叶斯估计中多维积分的近似方法一般可以分为两类:全局方法和局部方法。全局方法中不需要对概率密度函数做任何近似,只是将多维积分用特定的数值仿真的方法进行近似求解,例如,网格滤波算法(Grid-based Filter,GBF)[1]和粒子滤波算法(Particle Filter,PF)[2]。局部方法是指对递归贝叶斯估计框架中概率密度函数进行特定假设近似的方法,其中最常用的假设分布是高斯分布,如高斯埃尔米特卡尔曼滤波(Gussian Hermitian Kalman Filter,GHKF)[3]、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[4]、差分滤波(Divided Difference Filter,DDF)[5]、容积卡尔曼滤波(Cubature Kalman Filter,CKF)[6],高阶容积卡尔曼滤波(Highdegree CKF,HCKF)[7]和稀疏网格滤波(Sparse-Grid Quadrature Filter,SGQF)[8]等在内的多种次优非线性滤波方法,在各领域都取得了较好的应用效果[9-11]。
传统UKF算法基于对称采样原则,可调参数选为κ=3-n,可以从无迹变换(Unscened Transform,UT)传递的均值和方差中获得更丰富的高阶矩信息。但若n>3,κ为负值,UT传递方差时易出现非正定问题。为此,文献[6]在高斯滤波框架下提出了一种基于容积变换(Cubature Transform,CT)的CKF算法。实际上,从数值积分角度分析,将UKF的可调参数κ置零,便可得到CKF算法,由此证明CKF是一种特殊的基于对称采样的UKF算法。
事实上,CKF虽然解决了传统UKF的数值不稳定问题,但同时又引入了非局部采样问题。原因在于CKF采样时方差矩阵需乘系数,维数较高时,采样点距中心点的距离变大,影响了滤波精度。因此,如何同时解决UKF算法的数值不稳定和CKF算法的非局部采样是一个值得研究的问题。
为此,在分析CKF采样原理和CKF局限性的基础上,设计出一种正交变换矩阵,通过对CKF的采样点进行变换,进而导出一组新的采样点,并基于此提出了改进的CKF算法,以解决高斯滤波框架下算法存在数值不稳定和非局部采样的问题,最后通过非局部采样问题影响明显的系统模型验证了算法的有效性。
2 UKF与CKF的数值积分
考虑单位高斯分布权函数的数值积分[12-13]

用以下2n个加权采样点构造I[g(x)]的三阶精度的数值积分近似:
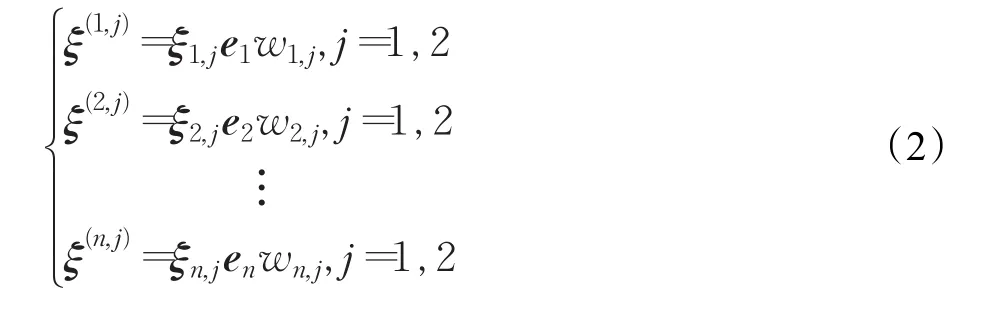
其中,ei表示除第i个分量为1外其他分量全为零的n维向量。式(2)满足以下关系:
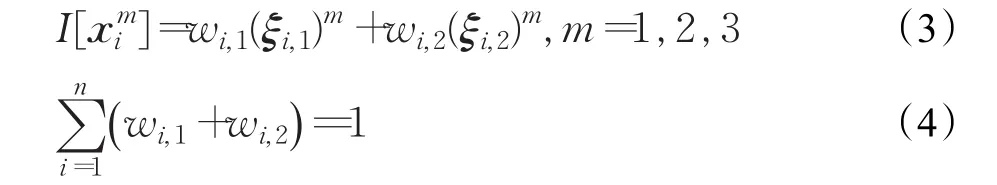
其中,标量xi表示向量x的第i个分量。
文献[4]导出的UKF算法用于近似单位高斯分布权函数的三阶精度数值积分的加权采样点为:

文献[6]导出的CKF算法用于近似单位高斯分布权函数的三阶精度数值积分的加权采样点为:

3 CKF算法的局限性分析
UKF算法中可调参数选为κ=3-n,对于维数n>3的非线性滤波问题,中心点处sigma点的权重为负值,容易导致传递的方差非正定,进而造成滤波算法的数值不稳定。Arasaratnam提出的CKF算法在高维问题中较UKF具有更高的精度和稳定性。
虽然CKF解决了UKF算法数值不稳定性的问题,但是自身又存在非局部采样问题。非局部采样问题是指基于采样点的非线性滤波算法,其使用的采样点偏离中心点(均值处)很大,造成滤波精度的下降。由式(5)看出,UKF中每个采样点与中心点的距离与成比例,κ一般取3-n,因此维数增加不会引发非局部采样问题。由于CKF没有可调参数对状态的扩张进行有效的抵消,每个采样点与中心点的距离与n成比例,随着维数的增加会产生非局部采样问题。
4 改进CKF的导出
为更好地说明非局部采样问题产生的原因,分析一个典型的UT过程。
考察如下非线性传递函数:


将每个sigma点经非线性变换进行传递:

传递后y的均值和方差分别为:

采用多元Taylor级数展开的方法对UT变换的精度进行分析。定义如下变量:

其中,σxi,j是σxi的第 j个分量。对式(9)中任意传递sigma点在处进行Taylor级数展开:

其中,∂/∂xj表示对应于x(jx的第j个分量)的偏导数。当 l=1时,式(14)可以表示为由于sigma点关于均值处是对称的,所以式(13)中所有奇次幂项都是零。根据式(10)和式(13),UT传递后的均值可表示为:

根据文献[14-15],传递后的均值可精确到三阶,而误差只在四阶及其以上的信息中引入。对UT传递均值的第 j个分量,其四阶及以上信息可表示为:

其中,hom()
κ表示这些高阶信息是可调参数κ的函数。对于CKF而言,κ=0,上式可进一步表示为:

从以上公式的推导过程可以看出,随着维数的增加,CKF传递均值的高阶信息显著增加。在实际应用中,真实值的高阶矩信息是未知的,因此使用UKF或CKF计算的均值的高阶矩信息可能更接近真实信息,也可能偏离真实信息[16]。相对于某一算法最优表现,更关心的其最差表现,对于基于采样点的非线性滤波算法而言,使其高阶信息趋于0不失为一种好的选择。基于以上讨论和认识,下面导出本文所要提出的基于采样点正交变换的改进CKF算法。
由式(2)可知:

ξ表示三阶精度数值积分公式中所采用的一组采样点集,满足如下关系式:
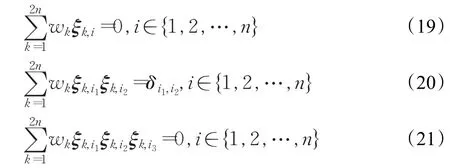
其中,ξk表示ξ点集中的第k个向量,ξk,i表示向量ξk第i个元素。一般研究等权重对称分布的采样点,如果ξ中每个采样点都是等权重对称分布的话,式(19)和式(21)是自然满足的。因此在构造三阶精度数值积分公式中等权重对称分布采样点时只需考虑式(20)。
式(20)对应的矩阵形式为:

对一组采样点进行正交变换不会改变其对性,因此Cξ自然满足式(19)和(21)。将式(22)中ξ替换为Cξ可得

因此Cξ也是三阶精度数值积分公式中所采用的一组采样点,则有如下结论:
假设ξ是三阶精度数值积分公式中所采用的一组采样点集,C是与ξ行维数一致的正交矩阵,则Cξ也是三阶精度数值积分公式中所采用的一组相同权重的采样点集。
定理1n×n矩阵B其列集的形式为:
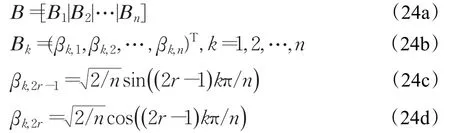
证明(1)首先假设n是偶数,则:
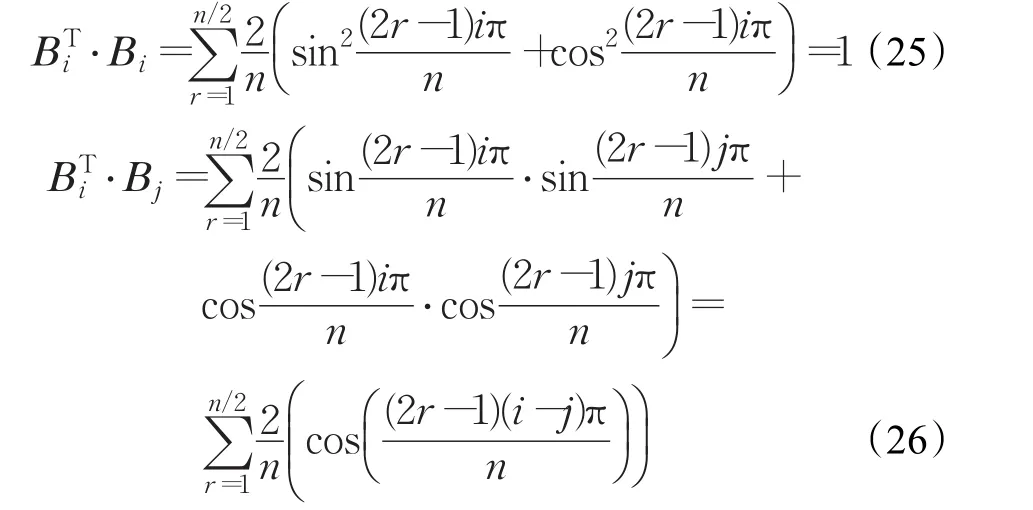
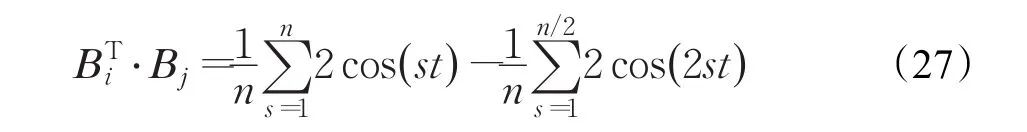

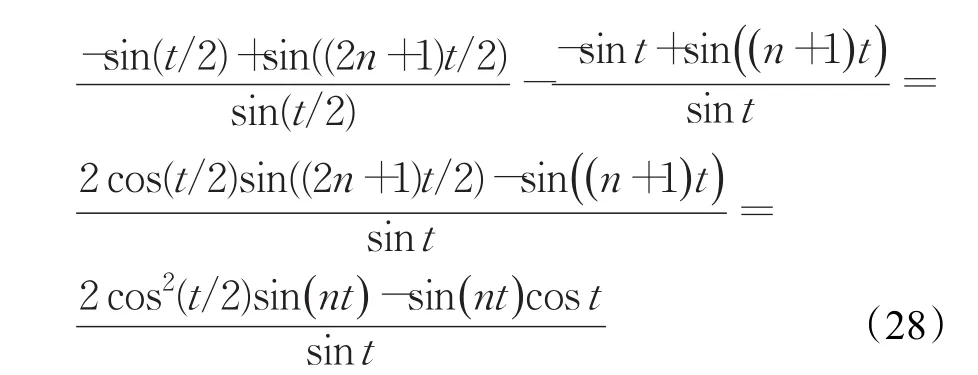


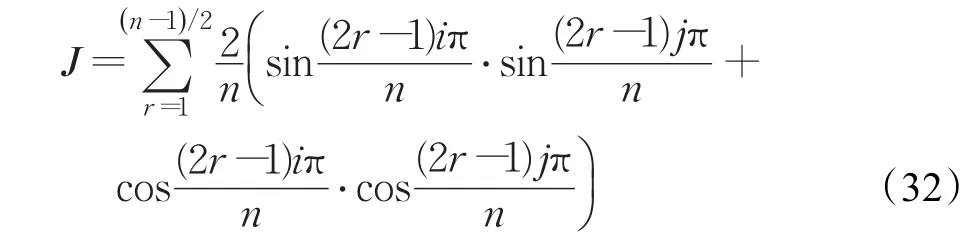

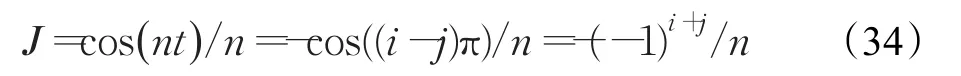
因此

综合式(30)和式(35)可得 B⋅BT=In。综上,定理得证。
可以利用式(24)中的正交矩阵B对CKF中的采样点进行正交变换得到一组新的满足三阶精度数值积分公式的采样点。为了使得到的新的采样点不存在数值不稳定问题,利用B对式(19)中的cubature点进行正交变换。
首先将式(6)中的cubature点表示成矩阵形式:

则ξ经B正交变换后为:

利用正交变换矩阵B对CKF中的sigma进行变换,即可得到一种新的高斯滤波算法——ICKF(Improved CKF)。
5 仿真验证
5.1 维数可变的强非线性系统
考虑如下维数可变的强非线性系统模型:


图1 改进CKF算法流程示意图
其中,xk是n维高斯随机变量,n可变;系统噪声wk-1~N(w;0,In),观测噪声为 vk~N(v;0,1)。为了比较不同维数条件下CKF和ICKF算法的性能,维数n的变化范围选取为1~50。仿真时间K=500,仿真时用于产生仿真数据的初始真值 x0=0.1×1n×1,其中 1n×1表示n×1维矩阵的每一个元素都为1。仿真的初始滤波条件设置为,各滤波算法的性能采用如下定义的评价指标进行比较。

其中,M=50表示Monte Carlo仿真次数,xk(1)表示xk的第一个元素。图2给出了不同维数下EKF、CKF、ICKF三种滤波算法的MRMSE。

图2 不同维数下三种滤波算法的MRMSE
从图2中可以看出,CKF和ICKF的滤波精度始终优于EKF,这是因为CKF和TCKF所使用的CT方法可以精确到三阶,而EKF中所使用的线性传递方法则只能精确到一阶。CKF算法的性能随着维数的增加而逐渐降阶,这说明CKF中通过cubature点传递所捕捉的高阶矩信息与真实值之间逐渐偏离。相反,ICKF算法中通过transformed sigma点传递所捕捉的高阶矩信息基本为0,因此基本不受维数变化的影响。
为了更加充分地说明ICKF相对于CKF的精度优势,图3给出了n=30时三种滤波算法50次Monte Carlo仿真的RMSE,图4给出了RMSE的均值和标准差。
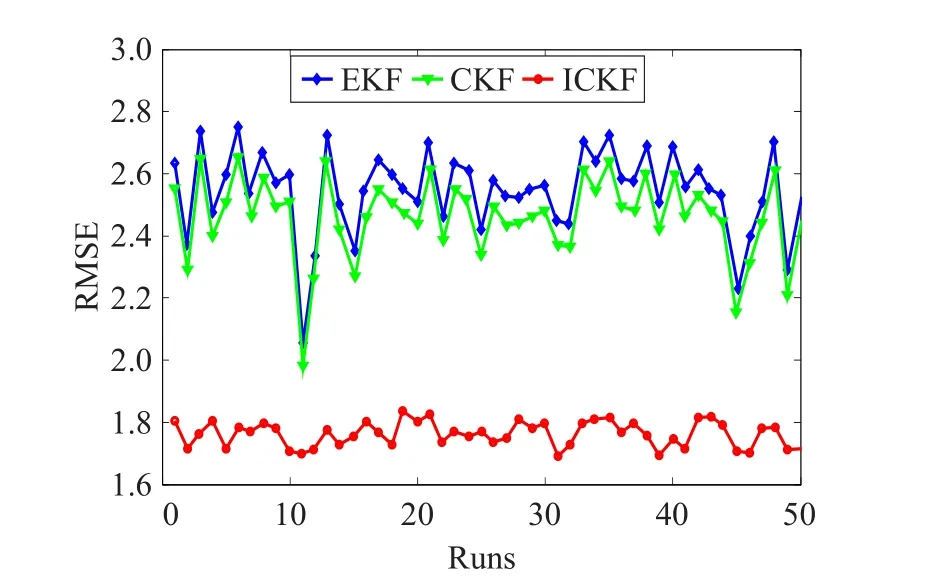
图3 n=30时50次Monte Carlo仿真的RMSEs

图4 50次Monte Carlo仿真的RMSEs均值和标准差
从图中可以明显看出,在高维、强非线性滤波问题中,ICKF相对于CKF具有更高的精度,从而验证了ICKF算法的有效性。
5.2 角测量跟踪模型
角测量模型描述的是一个二维平面内的动态目标跟踪问题,具体数学模型为:



为了公平地比较两种非线性滤波算法,进行100次独立Monte Carlo仿真实验并取其平均,图5给出了动态目标的跟踪轨迹。

图5 运动目标的跟踪轨迹
由图5可见,当初始协方差矩阵误差较大时,CKF和ICKF都能很快收敛,但ICKF的收敛速度更快,初始抖动更小,其跟踪轨迹也更为接近真实轨迹。
定义时刻的位置均方误差为:

类似的,定义k时刻的速度均方误差RMSEvel。位置和速度跟踪均方误差分别如图6和图7所示。

图6 位置跟踪均方误差

图7 速度跟踪均方误差
图6 和图7表明,ICKF对运动目标位置和速度的跟踪效果均更优,其初始误差曲线更为平滑、误差更小。
5.3 空中目标跟踪模型
将ICKF应用到空中目标跟踪系统中,并与CKF进行对比。假设目标在以未知角速度Ω等高度机动飞行,飞行高度h=10 000 m,运动模型为:


其中,T为测量时间间隔;高斯白噪声vk-1~N(0,Qk),协方差阵Qk=diag(M1,M1,M2),M1=q1T[T2/3,T/2;T/2,1],M2=q2TI,q1和q2为过程噪声强度参数。
坐标系原点的测量雷达获取目标的斜距η和方位角θ信息。测量向量为yk=[ηkθk]T,满足:

其中,wk~N(0,Rk)为量测噪声,为协方差阵,ση和σθ为雷达斜距测量噪声和方位角测量噪声的标准差。
定义均方根误差和均方根误差均值为:

表示位置、速度和转速的均方根误差及其均值,用于考察算法的跟踪性能。其中和分别为第i次打靶中第k时刻的目标真实位置和估计值;N为蒙特卡洛仿真次数;ς分别取为pos、vel和omg。每次仿真中所有滤波方法初始状态相同,进行100次蒙特卡洛仿真实验,仿真时间为100 s。
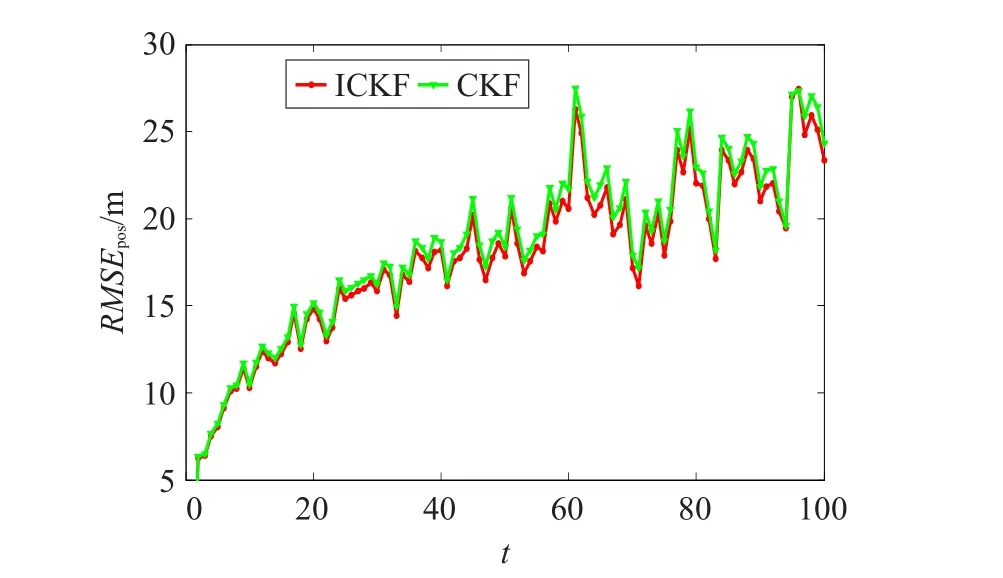
图8 目标位置估计均方根误差

图9 目标速度估计均方根误差

图10 目标角速度估计均方根误差
值得说明的是,所提改进算法是基于正交变化的改进CKF算法,所针对的问题是CKF算法应用于高维问题时出现的非局部采样问题而导致估计精度下降的问题。改进之处体现在对CKF算法的采样点进行了一次正交变换,没有改变采样点的个数和权值,在以上的仿真实验应用中,改进CKF算法所采用的采样点只需要一次定义即可,没有增加计算的复杂度,计算量与CKF相当。
6 结束语
本文提出了一种新的基于采样点正交变换的ICKF算法,由于只是对采样点进行变换,采样点的权值与传统CKF相同,保证了滤波算法的稳定性,经过正交变换后的采样点传递真实均值和方差的高阶矩信息基本为0,从而进一步提高了CKF算法在高维估计问题中的滤波性能。将此方法与现有的各种改进的CKF算法结合,可以取得更好的估计效果。
下一步的工作目标是将所提算法与已有的各种CKF改进算法相结合,更进一步地提高ICKF的滤波性能,并拓展其在诸如动基座的初始对准,惯性导航等领域中的实际工程应用。

