石膏矿矿柱失稳及顶板破坏过程力学分析

田 鹏

(湖南宏业石膏矿业有限公司)

石膏矿房柱式开采过程中的房柱损伤和顶板破坏是影响采矿安全的关键因素。杨涛波等[1]通过对多种铜矿体矿柱的力学分析并结合充人工矿柱强度理论，得到了人工矿柱的安全宽度范围。刘培正等[2]以某锰矿为研究对象，综合采用板梁理论力学分析及经验公式，并考虑矿柱的多重参数，得到了矿柱设计的基本方法且得到了良好的应用。相有兵等[3]针对某金矿矿柱回收致使顶板不稳的情况进行了相应的理论及工程模拟试验分析，得到了相应人工矿柱替代方案。王晓军等[4]通过理论分析得到了影响顶板临界厚度的因素，对各因素对顶板临界厚度的影响进行了数值模拟，最终得到了散体介质下矿柱上采临界厚度的预测公式，并通过工程应用验证了该公式的正确性。张钦礼等[5]以某矿为工程基础，运用尖点突变理论构建了采场破坏失稳模型,得到了导致矿柱失稳的主要因素，并从必要和充分2个方向验证了尖点突变理论的可行性。刘诗杰等[6]以H-K体为岩体本构模型,计算了因矿柱流变造成的顶板沉降过程，得到了沉降过程的稳定及持续时间，通过对某矿事故的过程计算，验证了计算模型的可靠性。卢宏建等[7]利用非接触全场应变检测设备分析了开挖扰动下硬岩矿柱破裂失稳的过程，揭示了矿柱损伤的演变过程，提出了状态监测及相应状态的控制措施。现有研究在不同的角度采用不同的方法对矿山开采过程中的矿柱、顶板稳定性进行了分析，总结了矿柱及顶板破坏失稳的因素，为安全开采提供了帮助[8-9]。涉及顶板稳定性分析的研究中，对顶板的空间效应因素方面考虑较少。针对大跨度矿房失稳，基于以上分析，运用突变尖点理论，得出矿柱失稳判据，将采场顶板视为薄板，运用里茨法分析顶板破断机理。

1 矿柱失稳判据的建立

矿柱在复杂应力反复作用下内部应力也逐渐增加，当达到疲劳破坏的极点，矿柱边缘就会出现垮落破坏，进而会演变为突变性失稳。随着开采活动的进行，矿柱中的应力开始变化，当矿柱内部应力逐渐增加时，矿柱边缘开始垮落，随后，矿柱会发生突变性失稳。从矿柱的应力峰值到矿柱边界这一区段，矿柱应力超过了屈服点，称为屈服带(或塑性区)。见图1。

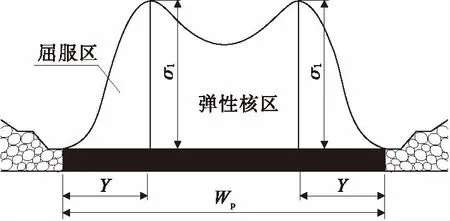
图1 矿柱屈服带及弹性核区

矿柱屈服带向里的石膏岩体应力没有超过屈服点，符合弹性法则，称为矿柱的弹性核区。塑性区宽度为Y，弹性核区宽度为Wp-2Y。设条带开采的采深为H，上覆岩层容重为γ，条带矿柱的宽度为Wp，采宽为Wm，建立条带矿柱的力学模型(图2),则矿柱的实际载荷为

(1)

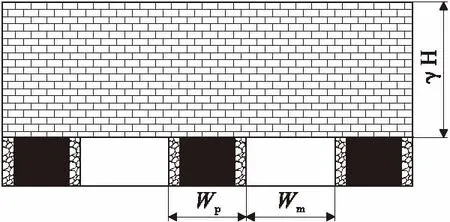
图2 条带矿柱力学模型

矿柱弹性核区与屈服区域的本构关系曲线是不同的。矿柱屈服区域的本构关系为

σ=Eε(1-D) ,

(2)

(3)

式中，ε、εmax为常数;E为初始弹性模量。

在矿柱屈服带内，矿柱高度为h,载荷Ps与变形u之间的关系为

(4)

式中,u0为峰值载荷所对应的变形值。

在矿柱弹性核区，载荷Pe与变形u之间的关系为

(5)

根据上述分析，矿柱内塑性区的应变能V1和弹性核区的弹性势能V2分别为

(6)

(7)

上覆岩层的自重势能V3为

(8)

根据以上力学模型的分析，图2所示模型系统的总势能函数为

(9)

从系统的总势能表达式出发，以u为状态变量进行尖点突变理论分析。对V求一阶倒数，并令其等于零，得到平衡曲面M方程为

(10)

根据平衡曲面的光滑性质，求得尖点，在尖点处有如下关系：

(11)

对方程进行求解最终可得到本系统突变的分叉集方程为

(12)

当Δ≤0时，矿柱失稳;当Δ>0时，矿柱保持稳定。

2 矿房顶板稳定性变化研究

2.1 矿房顶板上覆岩层压力计算

关键层的破坏是造成顶板载荷变化的关键因素。采用组合梁结构计算上覆岩层载荷。设采场覆岩中有m层岩层，从下至上n(n≤m)层同步变形，每层岩层的厚度为hi，体积力为γi(i=0,1,2,3,…,m)。关键层载荷计算模型见图3。

由于有n层岩层能同步变形，由叠梁理论可知

(13)

式中,Mi为第i层岩层的弯矩；Ei为第i层岩层的弹性模量；Ii为第i层岩层的惯性矩。

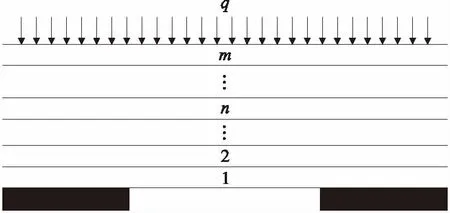
图3 关键层载荷计算模型

由式(13)可得，

(14)

其组合梁弯矩M为

(15)

对于第一层梁来说，将式(14)带入式(15)得到

(16)

薄板的受力微分原理为

(17)

可得

(18)

式中，q为全部(n层)控制岩层的自重载荷。

将q和Ii的具体表达形式带入上式得

(19)

2.2 采场顶板破坏过程力学分析

顶板的空间效应是分析大跨度及某个矿柱失稳导致大面积顶板断裂的关键，目前的理论尚不能较好地解释上述情况。将顶板简化为弾薄板，并运用里茨法理论来分析其破断规律[10]。采矿过程中形成的顶板一般都是矩形。因此，这里采用四边固支矩形薄板对采空区顶板进行分析。假设顶板上覆岩层压力为q1，设矩形薄板的长边为2la，短边为2lb,顶板的厚度为h1，顶板岩体的弹性模量为E，泊松比为μ，抗弯刚度为D，极限弯矩为Ms。四边固支矩形顶板的力学模型见图4。

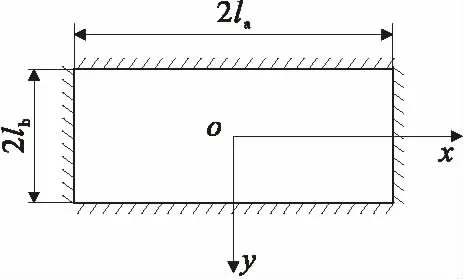
图4 四边固支顶板力学模型

基于弹性力学的最小势能原理，采用里茨法构建满足边界条件的一阶挠曲面方程为

(20)

根据薄板弯曲的直法线假设，求得薄板弯曲总势能为

(21)

由(∂Ep)/(∂A1)=0,得出A1，进而求得ω。

根据弹性力学的内力弯矩公式，求得等厚薄板的弯矩为

(22)

(23)

其中，

(24)

(25)

(26)

运用极限方法对式(22)和式(23)求极值，可以得到矩形薄板的最大弯矩值。最大弯矩在薄板长边中点，因此，若顶板发生破断，最先出现在长边中点，裂纹由中点向边缘扩展，直至整个边缘发生破断。

随着长边裂纹的不断发展，会出现两边固支两边简支的情况。力学模型见图5。

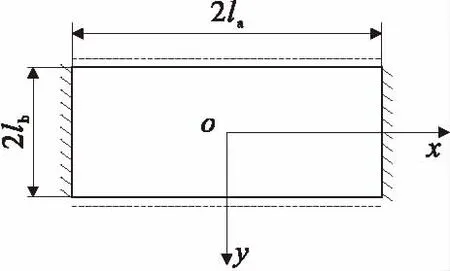
图5 两边固支两边简支顶板力学模型

同样利用里茨法构建满足上述边界条件的一阶挠曲面方程，即

(27)

利用弹性力学的内力弯矩公式，求得薄板的弯矩为

(28)

(29)

计算可得顶板弯矩的最大值点在短边中点，然后逐渐向两端扩展，原固化边形成简支边，顶板形成“O”型破坏。

随着采矿活动的进行，矩形顶板的4条固支边全部发生断裂破坏而成为简支边。此时顶板的破断形式发生改变。因此，需重新构建力学模型，对其破坏规律进行研究。新建模型见图6。

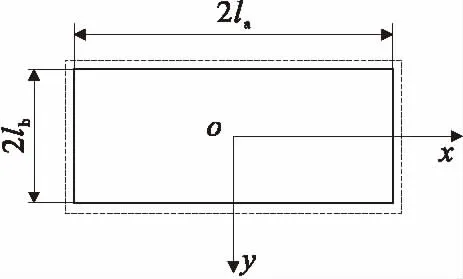
图6 四边简支顶板力学模型

利用里茨法构建满足上述边界条件的一阶挠曲面方程，即

(30)

利用弹性力学的内力弯矩公式，求得薄板的弯矩为

(31)

(32)

计算可得破裂发生在弯矩最大处,即薄板中心，并沿x方向扩展至短边边缘分叉，继续扩展，形成“X”型破断。

最终2种破断形态共同构成“O-X”破断形态。顶板破断的演化过程见图7。

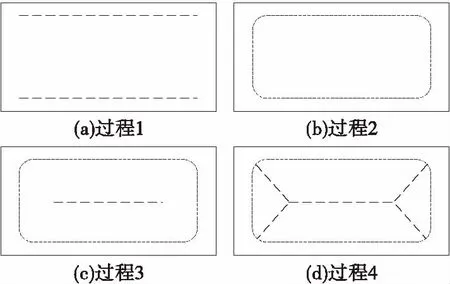
图7 采场顶板“O-X”破断演化过程

3 结 论

通过对矿柱失稳原理进行深入分析，并结合石膏岩体的损伤本构方程，推导出矿柱失稳判据。建立四边固支矩形顶板的力学模型，运用里茨法对石膏矿矿房顶板进行受力分析，随着采矿活动的进行，矩形顶板的4条固支边将发生断裂破坏从而成为简支边。因此，重新构建四边简支矩形顶板的力学模型，并对其进行力学分析。最终得出石膏矿矿房顶板“O-X”型破断的演化过程，为保证矿柱顶板稳定提供了理论参考。