基于半张量积的企业创新网络演化博弈

武利琴，徐勇，王金环，李杰

网络上的演化博弈称为网络演化博弈，能够很好地刻画生物系统、物流系统、社会系统、多智能体系统的演化规律，引起了众多学者的广泛研究，如文献[1-4]就将网络演化博弈与各个系统紧密地联系在了一起。在一个网络演化博弈中，节点和边分别代表玩家和玩家之间的相互关系。在某些特定的策略调整规则下，玩家根据邻居上一时刻的策略和收益，不断更新自己下一时刻的策略。随着时间变化，整个网络演化局势和博弈动态都在不断变化。网络演化博弈理论有助于理解合作的涌现及演化规律，经常被用于研究经济管理方面的问题[5-6]。

当下经济发展背景下，企业唯有不断创新才能长久生存发展下去。由于创新成本高额，部分企业不愿意改变原有模式，每个企业都想追求自己的收益最大，然而对于政府或者整个社会来说，所有企业全部创新，才是最好的局势。当前已有一些对企业间创新博弈的研究方法，如文献[5-8]，通过构建微分方程组，利用给定的初始条件，得到方程组的解。该解描述了企业的总体构成P(创新比例)随时间的演化趋势，并通过数据仿真方法将博弈动态趋势以图的形态呈现[9]，然而并不能展示每一次博弈后整个企业网络的博弈动态。

本文通过构建精确的理论框架来分析和控制企业创新网络演化的博弈动态，获得每次博弈后各企业的收益、策略等性质，主要运用了矩阵半张量积这种新的方法。半张量最先由程代展教授提出，成功应用于逻辑网络的分析与控制[10-13]，包括布尔网络稳定性、可控性、可观测性及最优控制[14-17]。半张量积在网络演化博弈动态行为及策略最优控制方面的研究也取得了显著成果[18-20]，并在智能电网、经济破产机制等实际问题中得到了广泛应用[21-22]。同时，也可用于企业创新方面的研究。

在企业创新网络中，本文将所有企业按规模分为大小两种企业，建立企业创新双层耦合网络。网络中各节点不同时刻采取的策略不同，会影响整个网络的演化趋势。因此可通过政府调控使得整个网络都达到创新的稳定局势，并能永久保持下去。

1 预备知识

本节给出关于半张量积的常用符号、定义和基本性质。

定义1[10]设为与的最小公倍数，那么与的半张量积定义为

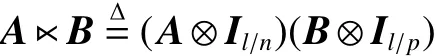
半张量积是普通矩阵乘积的一般化, 因此通常省略半张量符号”。

定义2[10]设。它们的Khatri-Rao 积, 记, 定义为

命题1[11]1)设及为两列向量，则，其中维矩阵被称为换位矩阵, 且；

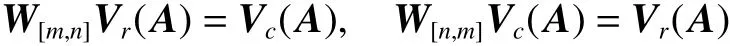
引理1[18]假设和，则有，其中。

引理2[11]设是一伪逻辑函数, 则存在一个唯一的矩阵, 称为的结构矩阵, 满足

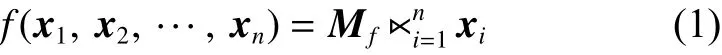
引理3[11]考虑一个值逻辑动态网络：

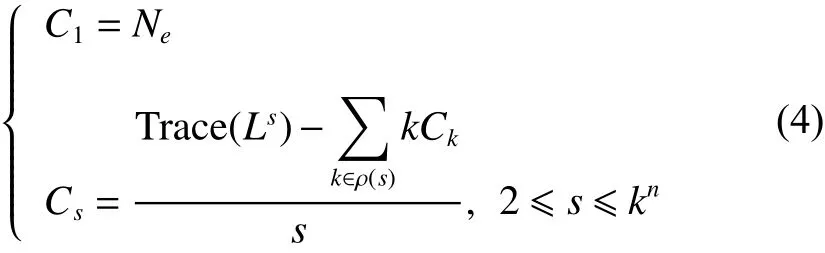
2 企业创新网络演化博弈

本文主要考虑企业群体之间的创新问题。企业创新成本投入和风险承担是必需的，由于其规模不同，导致资金周转与风险抵御能力的差距巨大，因此将“智猪博弈”作为基本博弈是非常适合的。将参与博弈的企业群体按照规模分为两类：大企业和小企业。将每个企业作为网络中参与博弈的玩家，从而构建企业创新双层耦合网络，上层表示大企业群体，下层表示小企业群体。假设双方创新成本为2，收益均为10。博弈分为4种情况：若大小企业都创新，双方获得创新收益比为7∶3；若仅大企业创新，小企业可剽窃大企业的创新成果，并抢先占领市场，两者创新收益比为6∶4；若仅小企业进行创新，大企业可凭借其规模效应获得更大的利润，两者收益比为9∶1；若大小企业都不创新，双方收益均为零。对应基本净收益矩阵：

2.1 企业创新网络博弈模型

对应上述双层网络演化博弈的过程构建模型。

2)基本网络博弈：由两个连通玩家(不同层)形成的基本博弈，且策略集，对应收益双矩阵：

3)策略更新规则：采用确定性无条件模仿策略更新规则。玩家i 在时刻的策略模仿它同层邻居在t时刻最优收益对应的策略，设

则

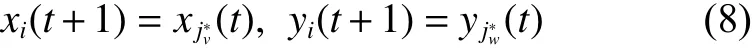
那么整个网络的策略更新表示为

4)策略模仿优先权：若3)内策略更新规则中被模仿的邻居玩家不唯一，令

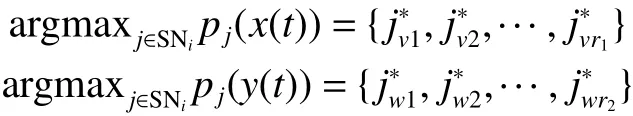
则优先权如式(10)：

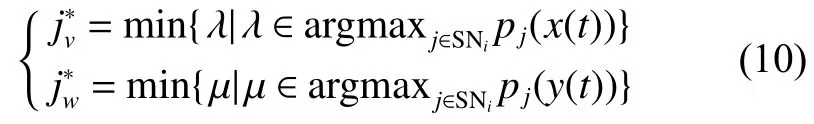
2.2 博弈动态演化分析

网络博弈随着时刻的变化不断更新策略局势，对应收益函数也发生变化，从而形成动态网络演化博弈。根据网络的拓扑结构，可得到企业创新双层耦合网络的邻接矩阵：

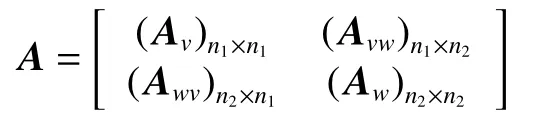
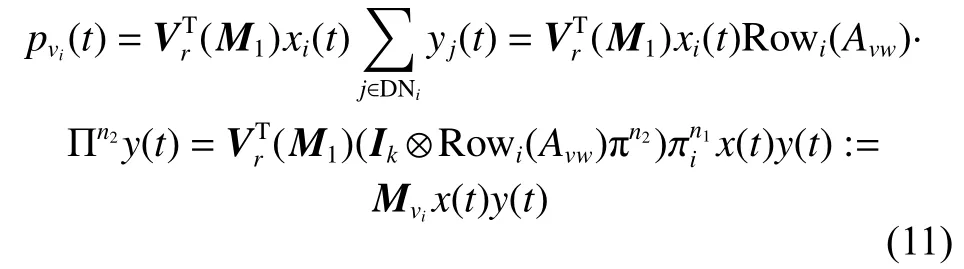
基于上述双层耦合网络演化博弈过程，考虑网络纯策略纳什均衡(本文策略选择是确定型的，因此在后文中全部简称为纳什均衡)的存在性，本文采用确定型策略更新规则。

定义3[18]对于一个博弈，一个策略局势是一个纳什均衡，如果满足对所有的均成立，其中是玩家集，是第i个玩家的策略集，且。

命题2[18]对于任给的，必然存在一个整数满足，其中是值逻辑算子的结构矩阵，且满足

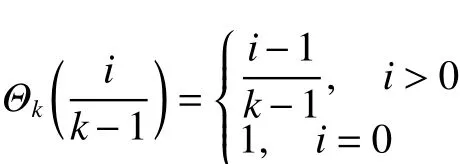
引理4[18]对于双层网络演化博弈G =(S1，S2)，支付函数满足式(11)、(12)，则存在一个纳什均衡，当且仅当存在一个整数，满足0，对应是所有纳什均衡的集合，其中对于，

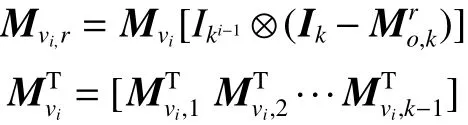
引理4只考虑了某一时刻该网络博弈的纳什均衡，而无法判断随着演化某些不稳定的局势逐渐演化为稳定的纳什均衡局势。因此，计算整个网络演化的转移矩阵是非常有必要的。

由引理2和支付函数表达式(11)、(12),可得到整个网络演化博弈的转移矩阵，步骤如下：

1)重写式 (11)、(12)为

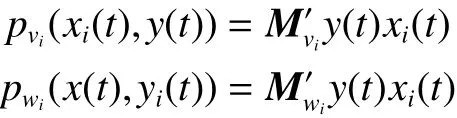
小企业玩家的最优反应策略为

3)根据优先权式(10)模仿同组邻居收益最大玩家的策略，有如下形式：

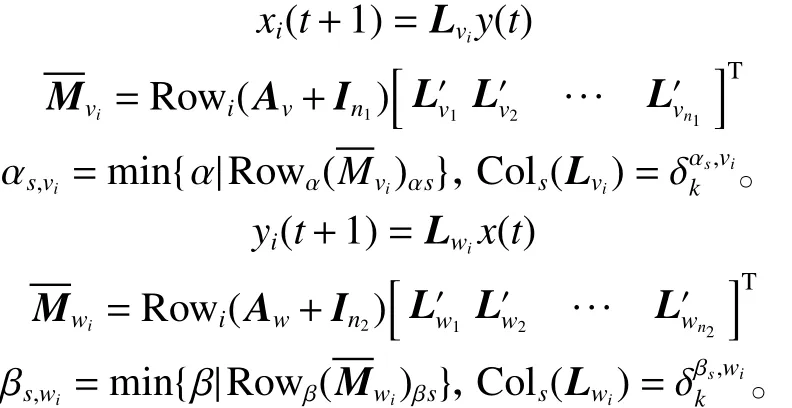
4)将3)中不同层的策略相乘，有

通过半张量积方法，由博弈动态方程式(13)可得到博弈结构矩阵。分析结构矩阵可得到博弈的稳定点、极限环，因此有定理1。

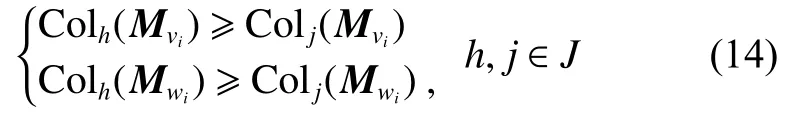
2.3 政府调控下的演化博弈

本部分通过政府调控改变基本博弈矩阵，从而使整个网络的演化达到理想的局势状态，即大小企业全部创新，且为稳定或者最优稳定纳什均衡状态。大小企业选择创新，由于投资成本过高，且收益相对减少，短时不能获取到创新带来的收益，因此政府通过调控诱发企业选择创新策略是非常必要的。控制设计如下。

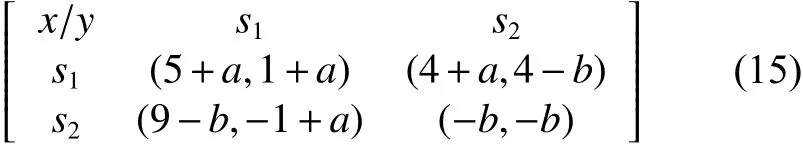
上述控制表示政府对企业的补贴与惩罚是同时进行的。设计控制的宗旨是政府对企业创新只起调控作用，尽可能少地进行投资或者获利。因此可假设补贴力度与惩罚力度相同，即。

博弈矩阵改变后，重新计算式(13)，可得博弈的转移矩阵L，通过定理1和推论1分析博弈的演化性质。若达不到所有企业全部创新的理想状态，则调整控制力度，直到大小企业玩家全部选择创新策略。

上述调控借鉴了“智猪博弈”中防止小猪搭便车，促使大猪小猪都行动的思想，即政府通过同时对创新企业进行补贴，对不创新企业进行惩罚，从而干预企业的创新决策，促使大小企业全部创新。

3 举例分析

本节主要通过举例，研究增加政府调控后整个企业创新网络的演化动态。

为了计算简便，以3个大企业和2个小企业组成的企业创新网络为例，分析演化博弈过程。网络拓扑结构图如图1所示，其中第一层为大企业，；第二层为小企业，。

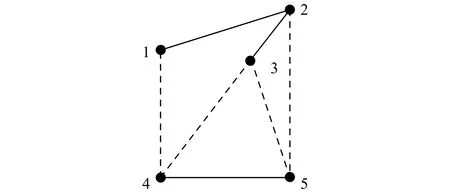
图1 不同规模企业博弈结构图Fig. 1 The game structure graph of different scale enterprises

根据网络拓扑结构图，我们可得到网络的邻接矩阵：

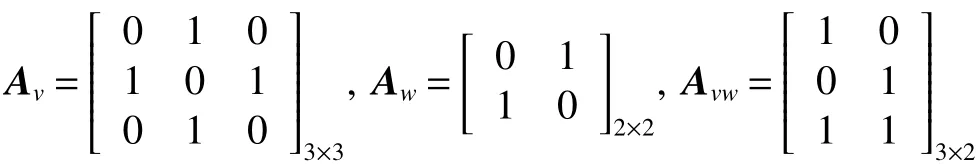
首先，根据引理4中的计算，有

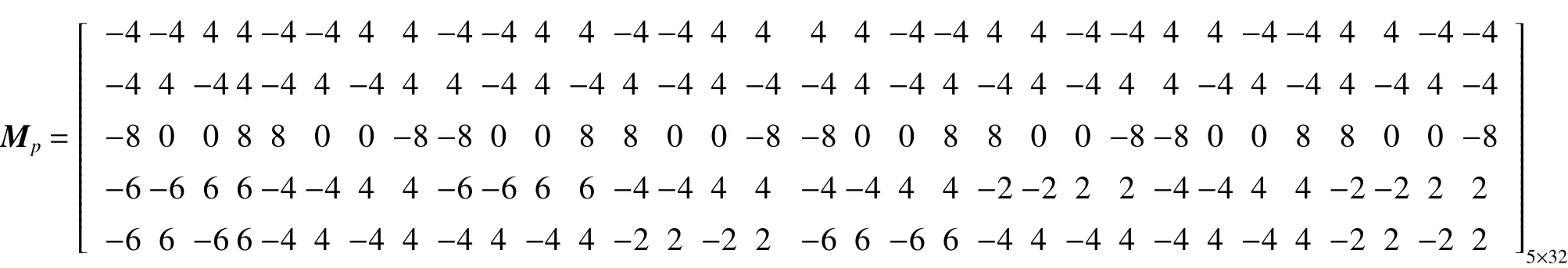
其次，由博弈动态方程

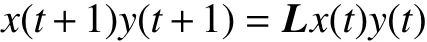
得到L为

比较上述两种情形可知，政府对企业的调控，有效遏制了小企业“搭便车”的行为，从而促使大小企业实现全部创新。

4 结束语

本文将所有企业按规模分为大小两种企业，建立企业创新双层耦合网络。运用矩阵半张量积方法，以“智猪博弈”为基本博弈, 得到每一时刻各企业的策略，整个网络局势演化随时间改变； 根据收益函数得到整个网络的最优稳定纳什均衡点； 最后，通过政府调控, 改变博弈的基本矩阵，从而达到最优稳定纳什均衡状态，即所有企业全部创新。