基于改进型BP神经网络的手部动作识别
尤波,李忠杰,黄玲
高性能仿人型假手对提高数以百万计上肢残疾者的生活水平具有重要意义,整套假手系统最重要的环节就是实现手部动作的快速准确识别。目前市场上绝大部分假手都是基于sEMG进行控制的。于是sEMG信号的采集、降噪、特征提取和分类器的设计等各个环节成为该领域国内外研究人员争相研究的热点,都取得了不错的成果。期间我们也做了大量的相关研究,例如杨文元等[1]用小波理论对sEMG信号进行处理分析,周丽娜等[2]设计了多功能肌电橡胶手识别系统。谢平等[3]采用自排序熵对不同动作模式下的表面肌电信号进行特征提取,并用其作为动作模式分类指标;邱青菊等[4]运用双谱分析法对表面肌电信号进行特征提取与模式识别。
对肌电信号进行降噪与特征提取的目的就是为后面分类器的设计提供更优质的数据,从而大大提高动作分类的准确率。常用于分类器设计的算法有 SVM(支持向量机)[5-8]、AdaBoost算法[9-10]、聚类算法[11-12]及神经网络算法等。张启忠等[5]运用球均值Lyapunov指数计算法,对肢体肌电信号进行特征提取与分类,用二叉树法构造了基于SVM的多类分类器。Kainz 等[13]对sEMG信号的低成本检索方案进行研究,并运用SVM对从传感器获取的信号进行分类。林海波等[14]对高斯核函数进行改进,并采用二叉树方法构建多类支持向量机完成12种上肢姿态的分类。杨帅[15]将AdaBoost算法运用在肌电信号的特征提取与分类上,并研究了在疲劳肌电信号干扰下算法的识别能力。
BP神经网络作为分类器,其应用同样广泛。例如,王尔申等[16]将BP神经网络和基本粒子滤波算法进行有机结合有效地改善了滤波性能;赵漫丹等[17]采用BP神经网络对AR模型的参数特征进行模式识别。近期国内外很多科研人员在研究深度神经网络在模式识别上的应用,识别准确率有了很大的提升。但深度神经网络训练时间长、计算量大、对硬件要求高,不利于识别系统的快速反应。因此,本文并未采用深度神经网络,而是对普通BP神经网络加以改进,以保证动作识别的快速性和准确性。
针对普通BP神经网络在训练过程中出现的学习过程缓慢以及过度拟合的问题,本文引入了交叉熵代价函数并对代价函数进行正则化处理。在实验中对sEMG特征信号进行模式识别,获得了较好的实验效果。
1 动作信号的模式识别
肌电信号识别是肌电研究领域中的一个重要方面,一般采用模式匹配原理来解决。手部动作的识别过程为:首先,将待识别的手部动作的肌电信号输入识别系统,经过预处理后用数学的方法提取sEMG特征信号,提取到的特征信号可以看成该动作的模式;然后将该动作模式同已知的参考模式进行比较,获得的最佳匹配的参考模式作为该动作模式的识别结果。动作识别具体流程如图1所示。
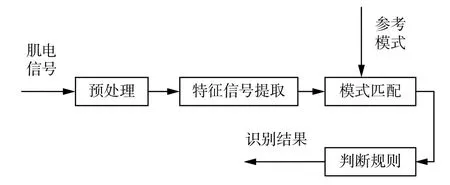
图1 动作识别流程Fig. 1 Motion recognition process
研究选取了环型抓取、捏取、五指伸展、竖拇指4种动作模式,用BP神经网络实现对这4类动作的有效分类,具体动作如图2所示。
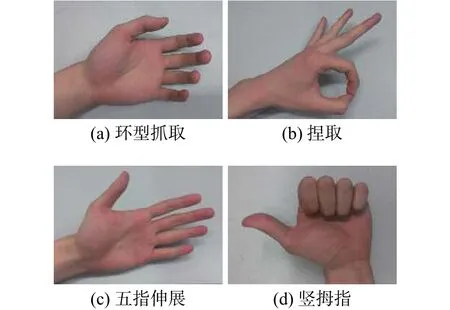
图2 4种手部基本动作Fig. 2 Four basic hand motions
2 改进型BP神经网络的设计
BP神经网络的英文全称为back-propagation neural network,即反向传播神经网络。在隐含层神经元个数可以随意调整的前提下,其可以逼近任意的非线性映射,且具有一定的容错能力,故适合作为肌电信号的分类器。BP神经网络包含输入层、隐含层和输出层3部分,具体网络架构如图3所示。
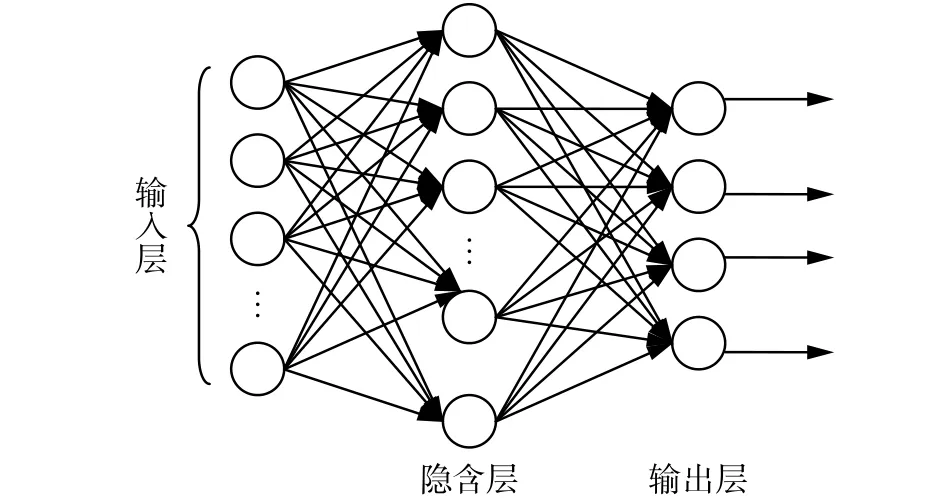
图3 BP神经网络架构示意Fig. 3 Diagram of BP neural network framework
改进型BP神经网络具体设计步骤如下。
1) 输入层和输出层节点的设计
因同一手部动作不同阶段的肌电信号所蕴含的特征存在差异,故可将不同阶段的4维数据进行拼接作为新的输入向量,以便为神经网络提供更多输入特征。但随着输入向量维度的增加计算量也随之增加,为保证系统的实时性,输入向量维度不能任意升高。综合考虑以上因素和实验验证,本文把所采集的N行4列数据重新组合处理成N/3行12列数据,即将4维数据升维至12维作为输入向量,输入节点数设置为12个。
因需要进行分类的手部动作有4种,故输出层的节点数设置为4个。
2) 隐含层节点数的设计
对于BP神经网络,有一个重要定理,即对于任何在闭区间内的一个连续函数都可以用单个隐含层的BP网络逼近,因而一个3层BP网络就可以完成任意的n维到m维的映射。隐含层的节点数目选择是一个十分复杂的问题,往往需要根据设计者的经验和多次实验来确定,因而不存在一个理想的解析式来表示。隐含层单元的数目与问题的要求、输入/输出单元的数目都有着直接的关系。隐含层节点数目太多会导致学习时间过长,误差不一定最佳,也会导致容错性差,不能识别以前没有训练过的样本,即泛化能力差。因此,一定存在一个最佳隐含层单元数。式(1)常用于选择隐含层最佳单元数:

3) 初始值的选取
由于系统是非线性的,由优化理论可知初始值对于学习能否达到局部最小和是否能够收敛的结果关系很大。一个重要的要求是:初始权值在输入累加值时使每个节点的激活值接近于零,权值一般取随机数,数值要比较小。输入样本也同样希望进行归一化处理,使那些比较大的输入仍落在代价函数梯度大的地方。
4) 代价函数的选择与改进
因为节点是通过改变权重和偏置量,并以一个代价函数的偏导数(和)决定的速率进行学习,故当神经网络学习缓慢时,实质是这些偏导数很小。普通BP网络使用的二次代价函数为


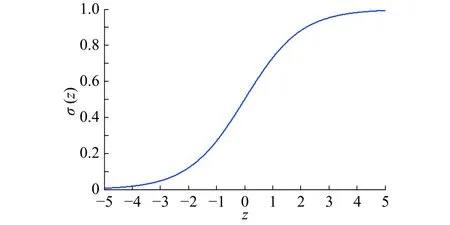
图4 Sigmoid函数Fig. 4 Sigmoid function image
由图4可以得出,当神经元的输出接近1时,曲线变化率接近0,故值很小,进而导致和很小,网络学习速率缓慢。于是,为了抵消对学习速率的影响,本文引入交叉熵代价函数:
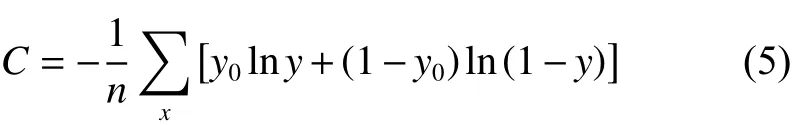
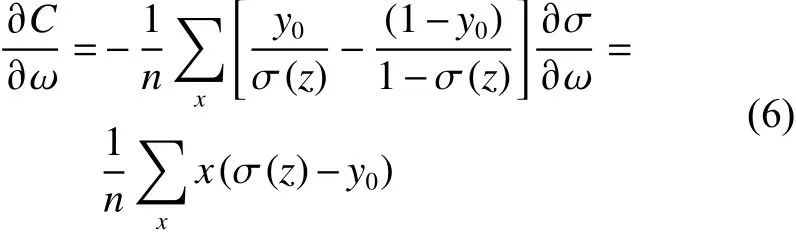
5) 对代价函数进行正则化处理
因测量误差不可避免,必然会导致额外噪声的产生。实验表明,系统学习局部噪声后,对特定的数据点可以表现得很好,但模型最终会在未知数据的泛化上出现问题,出现过度拟合的情况。常用的减轻过度拟合的方法有正则化、弃权和人为增加训练样本等,本文采用正则化方法。
正则化[18-20]后网络的权重相对较小,网络受限于根据训练数据中常见的模式来构造相对简单的模型,而抵抗训练数据中噪声的特性影响,并能够根据已经学到的知识很好地进行泛化。相比之下,未正则化的大权重网络可能会因为输入的微小改变而产生比较大的行为改变,从而会放大噪声对整个网络输出的影响,导致输出误差变大。
正则化具体公式:
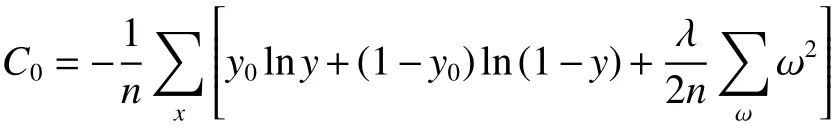
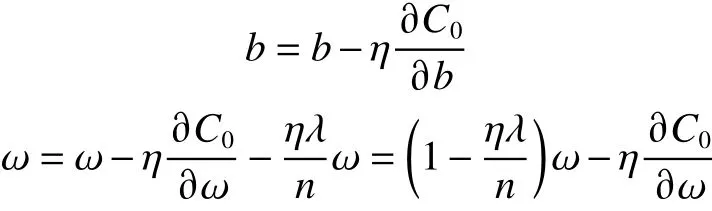
3 实验设计与仿真结果分析
3.1 肌电信号的采集
本文选取环型抓取、捏取、五指伸展、竖拇指等4种在实际生活中常用的手部动作作为模式识别对象。因与手部动作相关的肌肉群数量众多,根据所需识别的动作的特点以及大量实验检测发现,小指固有伸肌、拇长伸肌、指总伸肌、指浅伸肌等4块肌肉信号幅值变化最为明显,可涵盖大部分动作信息,故将其作为采集对象。表面肌电信号具体采集流程如图5所示,图6为采集系统硬件实物图。
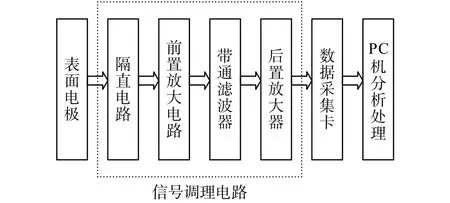
图5 表面肌电信号采集流程图Fig. 5 sEMG signal acquisition flow chart
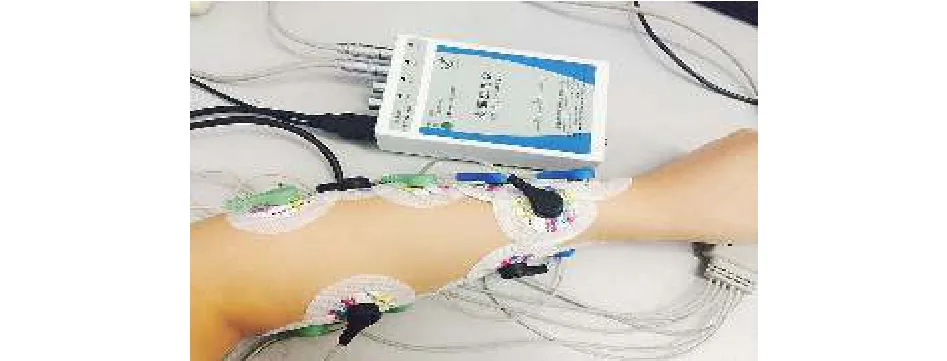
图6 表面肌电信号采集系统实物图Fig. 6 sEMG signal acquisition system physical map
实验选取3个被测试者,保证识别系统具有一定的广泛性。同一种动作模式下对每位测试者均采集500组数据,每组数据由4个通道同时采集,采样频率为1 000 Hz,并将每种动作所采集的数据按顺序标记为1、2、3、4。每完成10次动作后休息30 s,防止因肌肉疲劳产生信号畸变而导致额外噪声的产生。所采集的sEMG动作特征信号如图7所示。
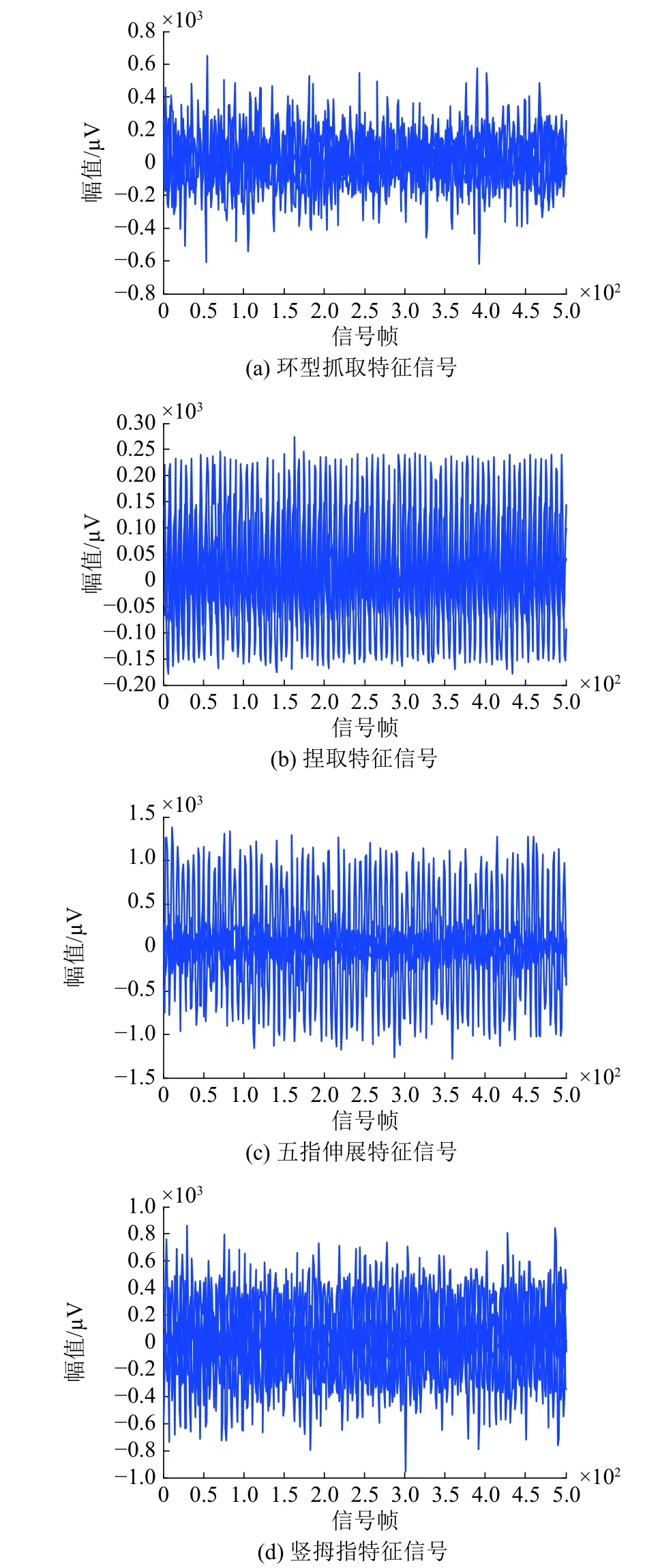
图7 4种手部动作肌电特征信号Fig. 7 Four kinds of hand-motion EMG signals
3.2 肌电信号的特征提取
常用的肌电信号特征提取方法有时域分析法、频域分析法、时频域分析法。由于实时性及可靠性的要求,所以这里采用时域分析法中的方差法,具体计算公式为

式中:N为sEMG信号采集的数据个数,x(i)为采集的数据段内的第i个sEMG数据,μ为有效数据段内肌电信号幅值的均值。在时域的分析与处理中,常采用去均值的白化过程,可以认为采集的sEMG信号是均值为零的平稳随机过程。因此,式(1)可以简化为
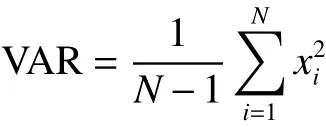
3.3 数据处理及仿真实验结果分析
根据BP神经网络理论,在MATLAB软件中编程实现基于改进型BP神经网络的sEMG特征信号分类算法。在采集手部动作过程的肌电信号时,不同时刻的数值差别很大,为消除各维数据间数量级差别,避免因为输入输出数据数量级差别较大而造成网络预测误差较大,需要对采集到的数据进行归一化处理,将全部数据转化为[0,1]之间的数。常用的归一化方法有最大最小法和平均数方差法。
1)最大最小法

2)平均数方差法
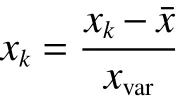
对网络的收敛性进行仿真实验验证,普通BP神经网络与改进型BP神经网络随着迭代次数的增加,代价函数收敛状况分别如图8、9所示。
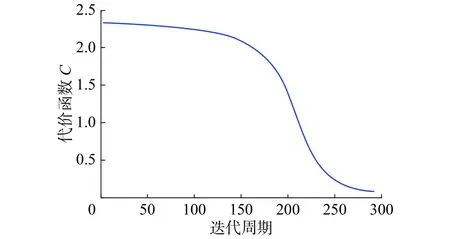
图8 普通BP网络代价函数曲线Fig. 8 Cost function curve of ordinary BP network
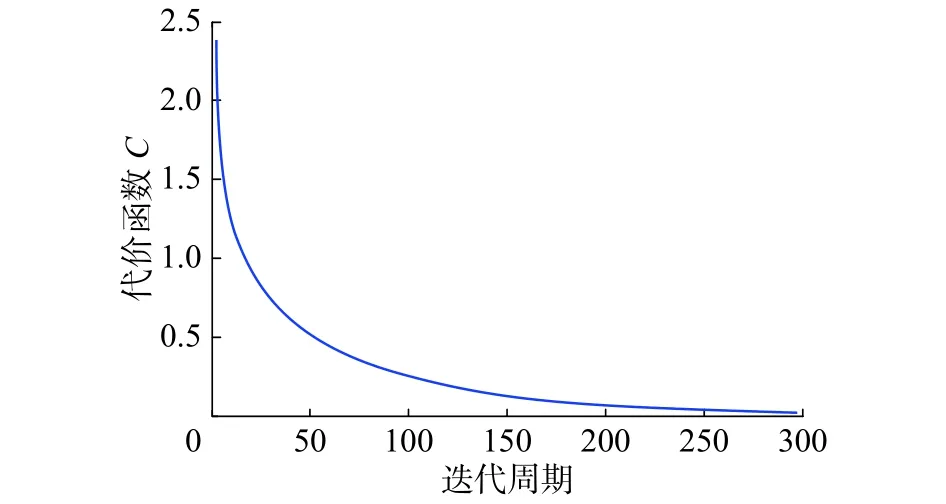
图9 改进型BP网络代价函数曲线Fig. 9 Cost function curve of modified BP network
对比图8和图9可知,改进型神经网络的代价函数是收敛的,而且整体收敛速度要比普通BP神经网络速度快,大大提高了神经网络的训练速度,达到了预期的效果。
BP神经网络分类算法程序具体执行流程如图10所示。
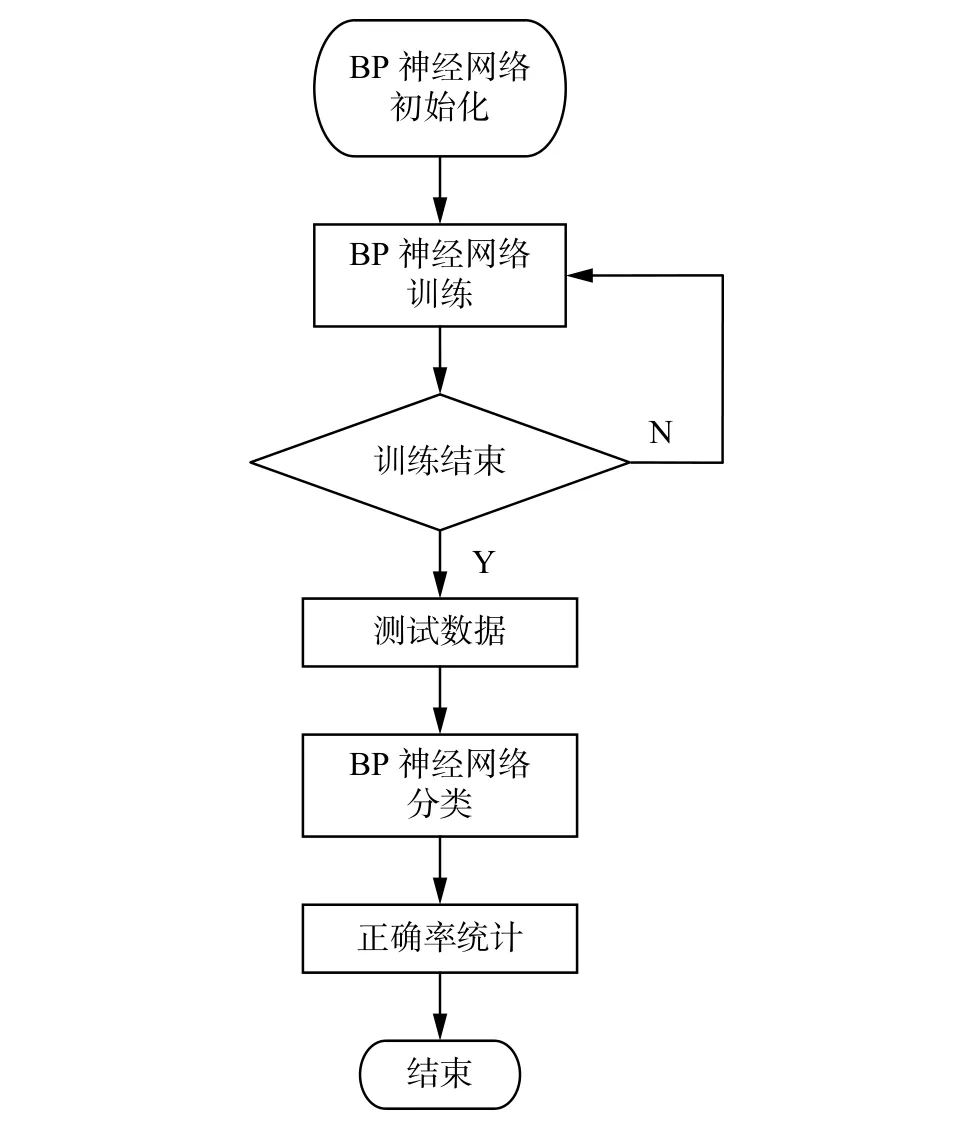
图10 程序执行流程图Fig. 10 Program execution flowchart
正确率统计公式为

为避免识别准确率的偶然性,本实验选取了500组测试数据,以保证样本处于较大状态。分别执行普通BP神经网络和改进后的BP神经网络所对应的程序,分类误差分别如图11和图12所示,横坐标为测试组别序号,对应的识别统计结果如表1所示。
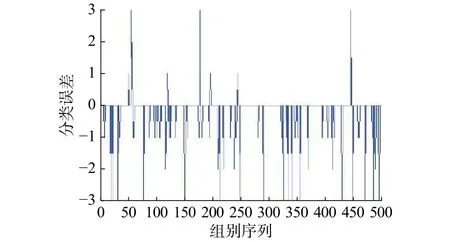
图11 普通BP神经网络分类误差Fig. 11 Classification error of ordinary BP neural network
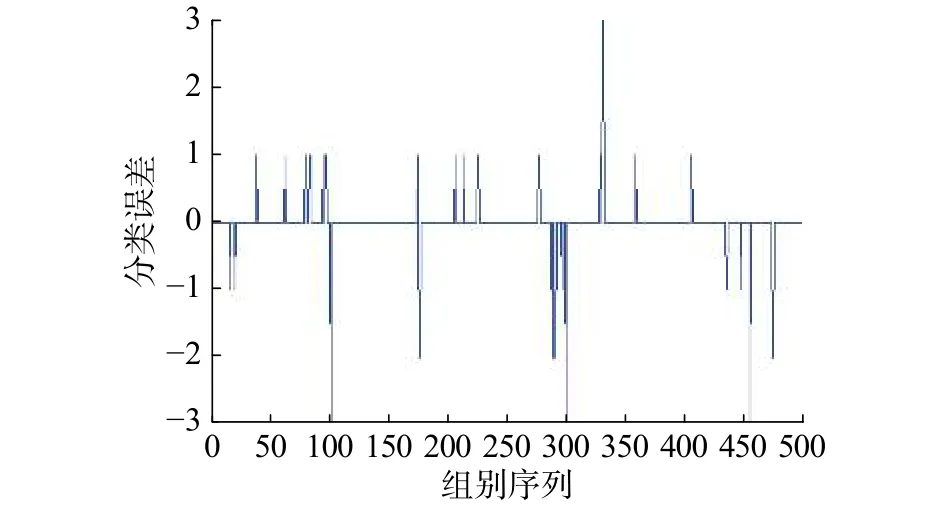
图12 改进型BP神经网络分类误差Fig. 12 Classification error of modified BP neural network
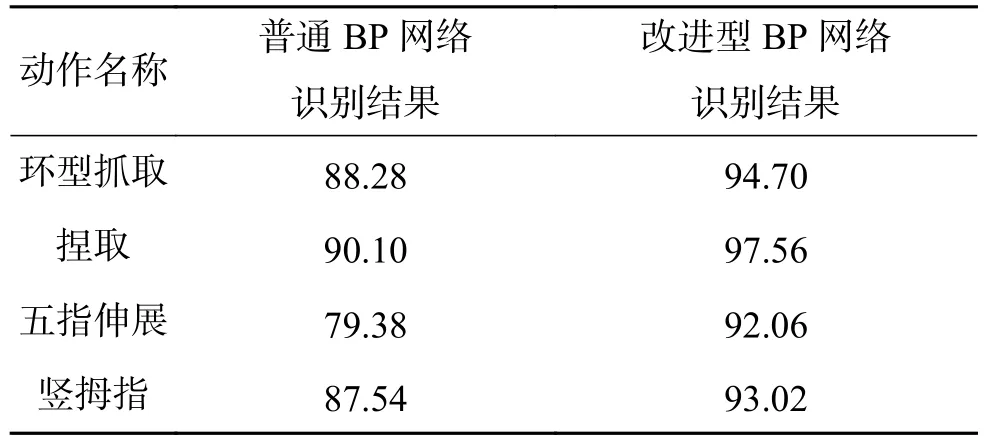
表1 识别准确率统计结果Table 1 Recognition accuracy statistics %
从图11和图12可明显看出,针对500组相同的测试数据进行分类识别,改进型BP神经网络的分类误差要明显小于普通BP神经网络分类误差。同时,表1的统计结果也印证了这一点。
进一步,对普通BP神经网络与改进型BP神经网络的分类时间进行统计。本文采用MATLABR2014a软件自带的计时功能对500组数据的分类时间进行统计,分别为62.387 s和46.869 s。平均每组数据识别所花时间如表2所示,识别耗时完全满足实时性要求。

表2 动作识别耗时结果Table 2 Action recognition time-consumption results
4 结论
本文使用改进型BP神经网络对环型抓取、捏取、五指伸展、竖拇指等4种手部动作进行模式识别,实验结果表明:
1)通过引入交叉熵代价函数,BP神经网络的学习速率得到了有效的提升,经少量迭代后代价函数值便迅速下降;
2)将输入端数据进行人工升维处理并将代价函数正则化后,网络的过度拟合现象得到了控制,泛化能力增强,动作识别准确率也得到了有效的提升。
同时,因高质量的训练数据可以使神经网络有更好的分类效果。故随着肌电信号采集硬件的改善,降噪、抗干扰能力的增强以及特征提取算法的优化,用于训练神经网络的数据质量会更高,改进型BP神经网络的模式识别能力也将会有更好的表现。

