深度神经网络在无源定位中的应用研究
, ,
(北京无线电测量研究所, 北京 100854)
0 引言
对于无源定位系统,常见的定位算法有测向时差定位、时差定位、时差频差定位等,大多数定位系统仅仅利用了不多于两种的测量信息,同时由于测量噪声的统计特性不准确,导致定位精度受到不同程度的影响[1]。
为了加强多源信息融合和定位系统的鲁棒性,文献[2-3]运用神经网络将接收到的信号强度与接收距离之间的非线性关系进行拟合,然后利用接收距离和位置坐标的方程关系进行求解。另外,文献[4]则将测量得到的时差和方向信息输入到神经网络中进行修正,然后利用定位算法进行求解。这些方法大多被运用在室内的无线定位中,空间范围较小,所使用的神经网络的层数也较少。与采用全连接神经网络不同的是,文献[5]使用的是径向基函数(Radial Basis Function, RBF)神经网络,场景和测量参数也比较简单,然而在较为复杂的环境中径向基函数神经网络这种浅层结构的建模能力有限,其拟合效果就明显不如深层的神经网络[6]。同时,上述几乎所有的文献都没有使用相应的泛化方法,仅仅用训练时的样本点作为测试,得到的结果不具有说服力。
本文将使用深度神经网络,将样本点的多种测量信息输入到神经网络中,通过改变输入参数的个数和神经网络的层数,并且运用正则化方法进行泛化,找到了最佳的超参数组合,并且与单层的全连接神经网络和RBF神经网络的定位精度进行了对比,仿真实验证明该深度神经网络模型可以提高定位精度和鲁棒性。
1 时差定位系统
1.1 模型建立
假设有3个雷达接收站,如图1所示,每个雷达接收站的坐标为Si(xi,yi) (i=0, 1, 2),辐射源的坐标为X(x,y),设辐射源到每个雷达接收站的距离为
Δri=||X-Si||,i=0,1,2
(1)
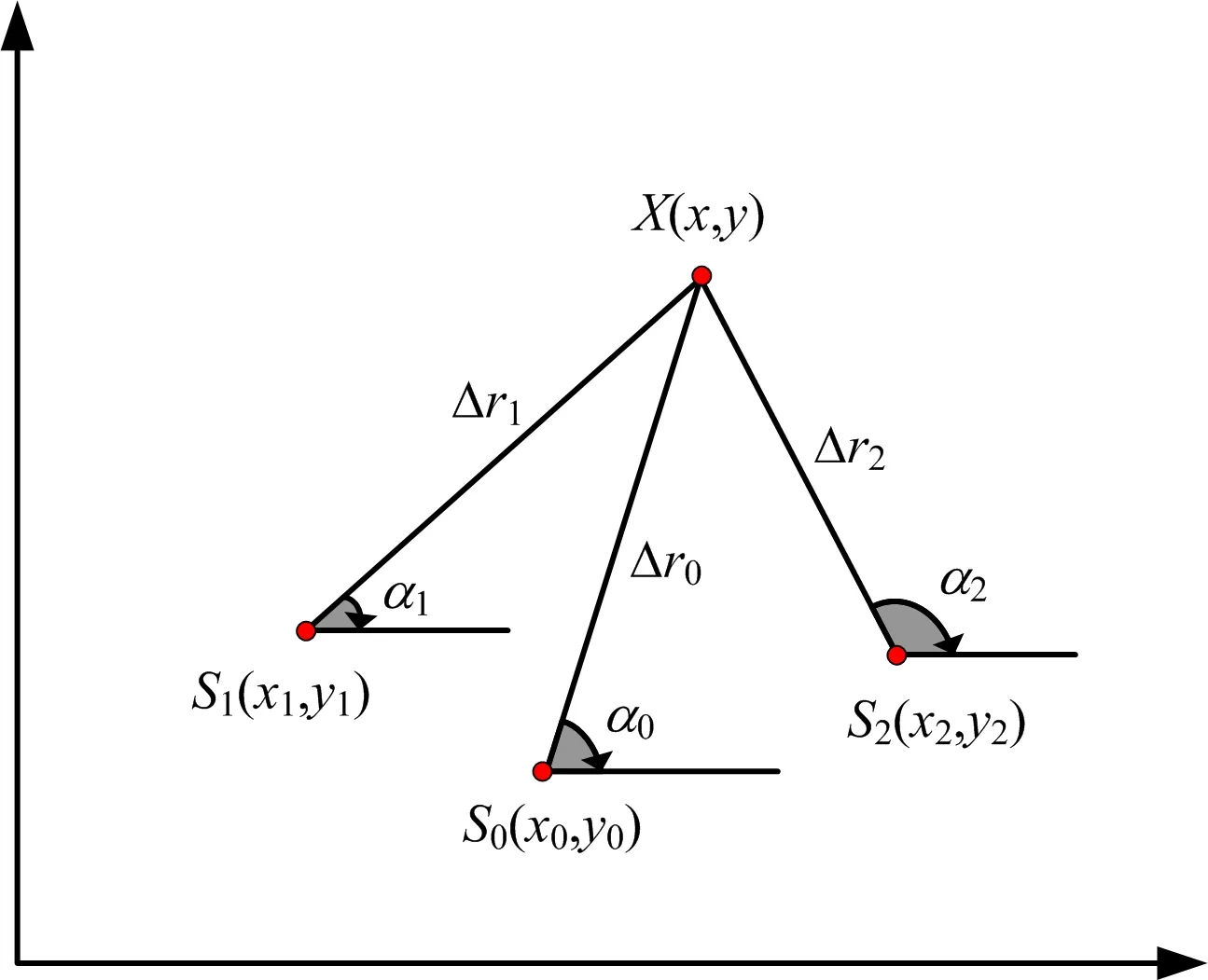
图1 三站时差定位示意图
每个雷达接收站到原点的距离为ri,以算出辐射源到任意两个接收站的距离差为
Δrij=Δri-Δrj,i,j=0,1,2,i≠j
(2)
为了便于分析并且不失一般性,以第一个接收站作为参考,可以得到两个互不相关的距离差:
Δrm0=Δrm-Δr0,m=1,2
(3)
将这些距离差公式组成一个方程组并进行化简,可以得到
(x0-xm)x+(y0-ym)y-Δrm0Δr0-
(4)
解方程得到辐射源的位置估计为
X=(ATA)-1ATF
(5)
式中,
利用式(5),得到x,y关于Δr0的等式。
进一步根据式(6)即可算出辐射源的位置:
(6)
1.2 定位精度分析
定位精度一般用GDOP来表示,也就是定位精度的几何稀释度,其表达式为
(7)
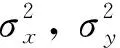
仿真设置:3个基站的坐标分别为S0(0,0) km,S1(0.5×1.732,0.5) km,S2(-0.5×1.732,0.5) km,时差均方根误差为20 ns,基站坐标均方根误差为0.5 m。
GDOP等值线图如图2所示。
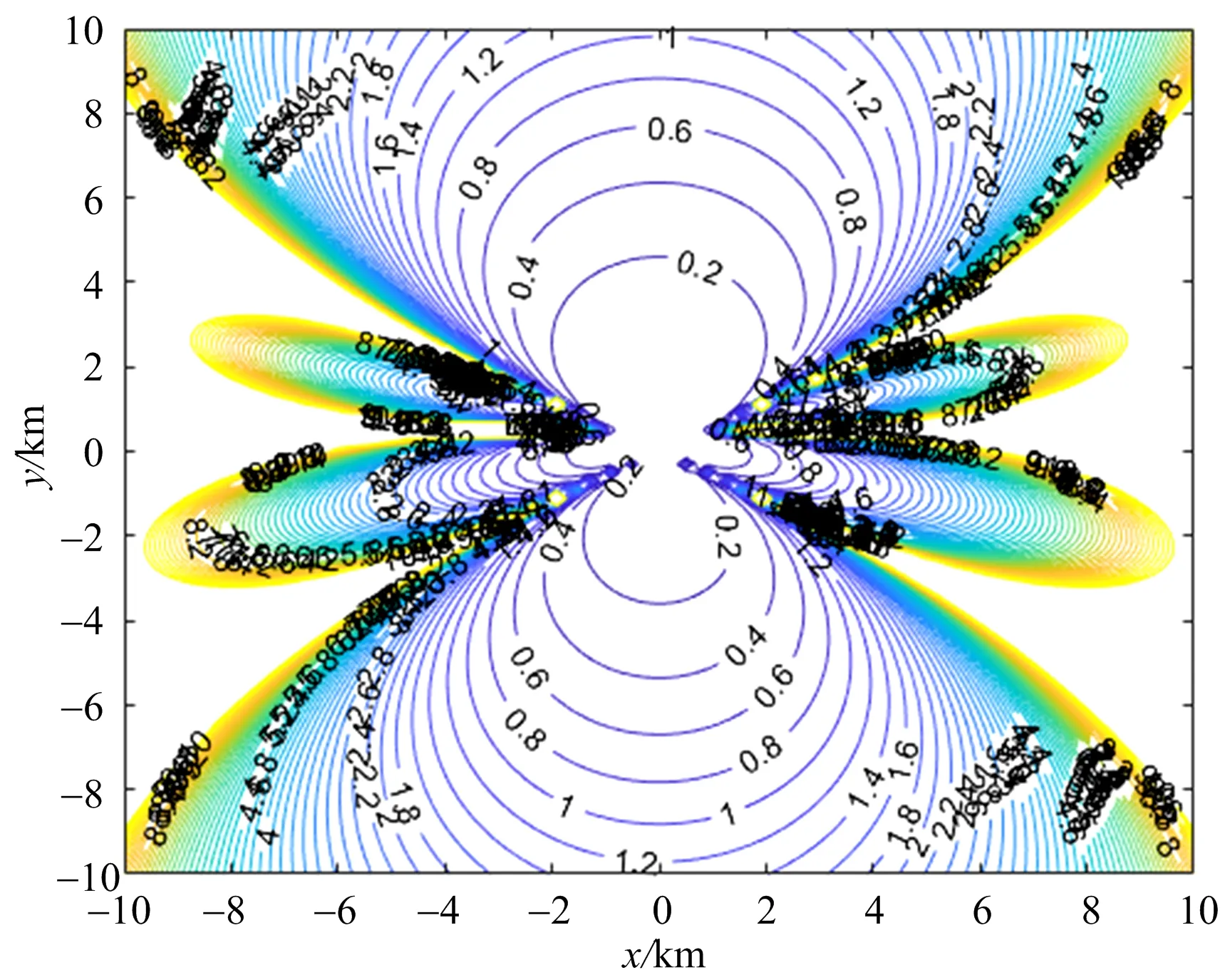
图2 GDOP分布图
2 深度神经网络定位
2.1 模型提出
神经网络是在20世纪提出来的一种模仿动物神经网络行为特征来进行分布式并行信息处理的算法数学模型。应用主要涵盖在图像处理、信号处理、模式识别、机器人控制等方面,其主要优点有:1)信息分布存储在网络内的神经元中,具有很强的鲁棒性和容错性;2)自学习、自组织、自适应性使得网络可以处理不确定或未知的系统;3)具有很强的信息综合能力,能同时处理定量和定性的信息,能很好地协调多种输入信息关系,适用于多信息融合和多媒体技术。
图3是一个含有1个输入层、1个隐藏层和1个输出层的神经网络示意图。其中输入层的神经元有3个,依次将其编号为1,2,3;隐藏层的神经元有4个,依次将其编号为4,5,6,7;输出层的神经元有2个,依次将其编号为8,9。另外在输入层和隐藏层的每一层都有一个偏置单元,图中用+1表示。这个神经网络为一个全连接的神经网络,每个节点都和上一层的所有节点有连接。比如隐藏层的节点4和输入层的3个节点1,2,3都有连接,其连接上的权重分别为w41,w42,w43。节点4的输出值a4的计算公式为
a4=f(w41x1+w42x2+w43x3+w4b)
(8)
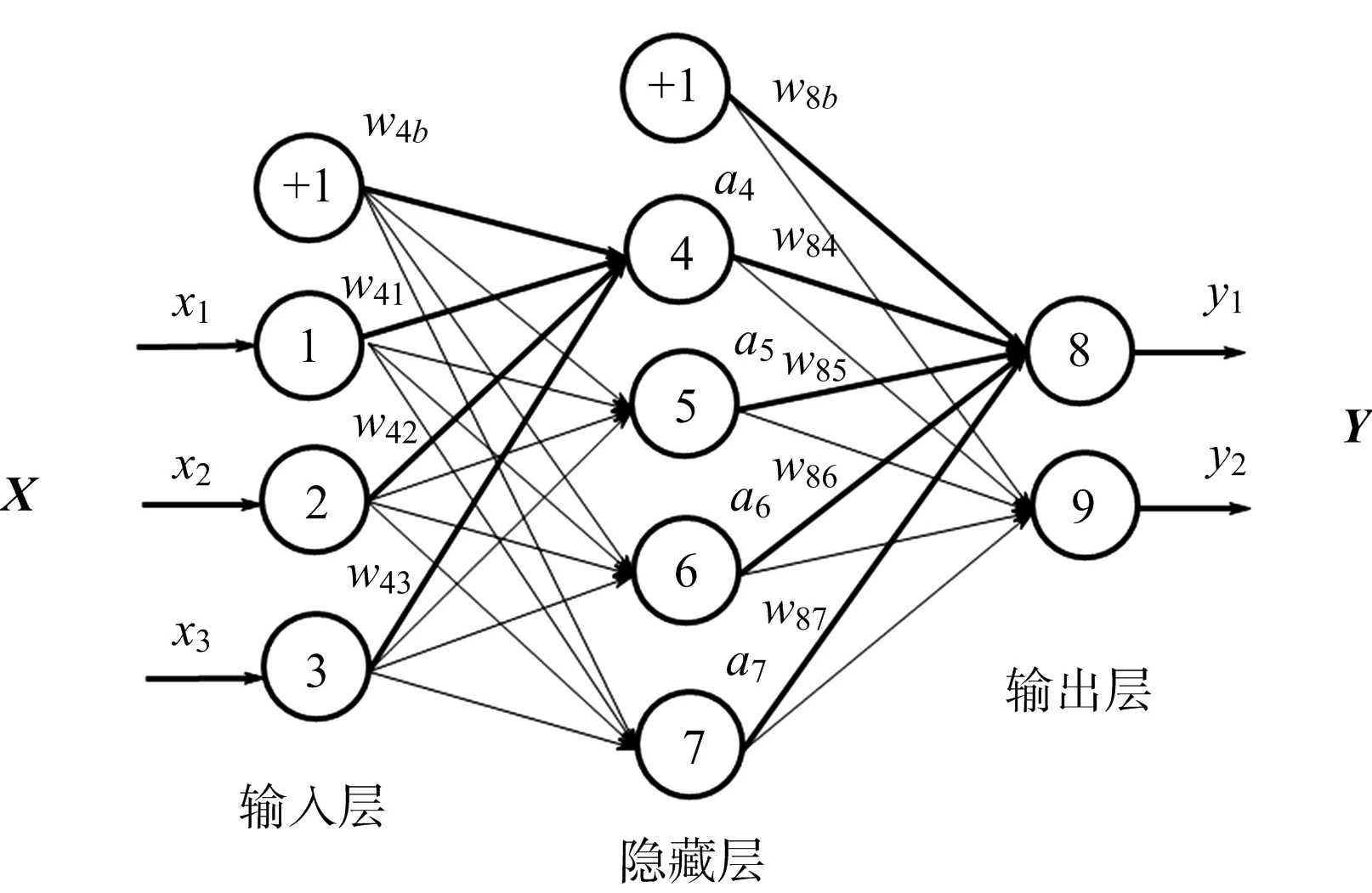
图3 神经网络示意图
式(8)中的w4b为节点4的偏置项,f为神经网络的激活函数,选取在深度神经网络中最常用的修正线性单元(Rectified Linear Unit, ReLU)函数。
同样,通过计算出节点5,6,7的输出值a5,a6,a7,节点8的输出值y1的计算公式为
y1=f(w84a4+w85a5+w86a6+w87a7+w8b)
(9)
图3所示仅为单隐层的神经网络,由于其拟合能力有限,因此可以通过增加隐藏层的个数,使其具有更好的表达能力。
2.2 模型训练
在-10~10 km的方形区域内以均匀分布的概率随机选取1 000个点的坐标值(x,y),然后算出时差值和方向正切值作为测量参数。为了模拟噪声环境并与图2形成对比;参考1.2节中的仿真设置,对时差加上均值为0、均方根误差为20 ns的高斯分布随机数,在方向角度值上加上均值为0、均方根误差为3 mrad的高斯分布随机数。最后得到无噪声和有噪声各1 000个样本点以及其对应的测量参数。
运用式(10)对输入的参数包括时差和方向角正切值进行归一化处理:
(10)
式中,μ为样本均值,σ为样本数据的标准差。
然后将这1 000个样本随机分为3组:训练样本组(600个)、交叉验证样本组(200个)、测试样本组(200个)。
损失函数设置为均方根误差(RMSE):

(11)
式中,x和y分别是样本中的真实坐标,xoutput和youtput分别是神经网络的输出坐标值。
然后将经过归一化处理的测量参数输入到神经网络中,参数个数依次为5(Δt10,Δt20, tanα0, tanα1, tanα2),4(Δt10, Δt20, tanα0, tanα1),3(Δt10,Δt20, tanα0),2(Δt10, Δt20)。
每个隐藏层的神经元个数为100个,得到训练结果如图4和图5所示。

图4 无噪声训练组RMSE与隐藏层个数的关系
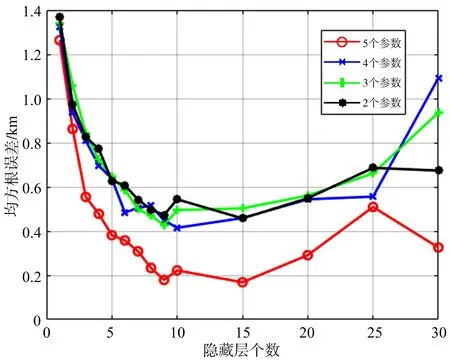
图5 有噪声训练组RMSE与隐藏层个数的关系
图4为无噪声训练组样本的隐藏层个数的增多与RMSE的变化关系曲线,从图4可以看出,随着隐藏层个数的增多,每条曲线的整体趋势是先下降后趋于变化缓慢最后又上升的趋势。在无噪声的情况下,当隐藏层的个数过多时,神经网络已经学习不到样本的特征,甚至会出现性能下降的情况。并且随着输入参数的增多RMSE值在逐渐减小,证明了神经网络对多源信息的综合利用。
图5为有噪声训练组样本的隐藏层个数的增多与RMSE的变化关系曲线,从图5可以看出,随着隐藏层个数的增多,每条曲线呈现出先下降后趋于变化缓慢最后又上升的趋势。说明在有噪声的情况下,当隐藏层的个数过多时,神经网络已经学习不到样本的特征,甚至会出现性能下降的情况。当输入参数个数由2个增加到3个和4个的时候拟合效果没有明显提高,但当增加到5个参数的时候,RMSE值有了明显的下降。
2.3 模型泛化
机器学习中的一个核心问题是设计不仅在训练数据上表现好,而且能在新输入上泛化好的算法。在机器学习中,有许多减少测试误差的策略,这些策略被统称为正则化,其以偏差的增加换取方差的减小。深度学习中正则化方法主要包括有范数正则化、提前终止、集成方法和随机失活(Dropout)[7]等,其中随机失活提供了正则化一大类模型的方法,计算方便但功能强大,是大量深度神经网络的实用集成方法,如文献[8]集成了6个神经网络赢得了ImageNet大规模视觉识别挑战赛(ImageNet Large Scale Visual Recognition Challenge, ILSVRC)。
针对以上几种正则化方法进行分析。提前终止是通过观测训练集和测试集数据的学习曲线进行手动操作的方法,使用简单但是需要大量人为干预,效果提升有限。文献[7]显示,Dropout比范数正则化方法更有效,它的另一个优点是计算方便,训练过程中产生n个随机二进制数与状态相乘,每个样本每次更新只需O(n)的计算复杂度,n代表模型中的神经元总个数。另外,文献[9]中将Dropout与其他的集成方法进行对比并得出结论:相比独立模型集成获得泛化误差,Dropout会带来额外的改进,是对集成方法的一种近似,计算复杂度也较小。
Dropout的另一个显著优点是具有广泛的适用性,几乎在所有分布式表示且可以用随机梯度下降训练的模型以及各种场景中都表现很好。例如文献[10]将其运用在贝叶斯神经网络中,文献[11]讨论了在循环神经网络中的使用情况,文献[12]研究了Dropout在长短期记忆网络中的应用。
无源定位通过对测量参数的运算得到目标的位置,其实质是一个在特定场景下将参数作为输入、将位置坐标作为输出的一个映射系统,又因为上文中提到的Dropout的各种优势,因此本文选择Dropout作为正则化方法来提高深度神经网络的泛化性能。
根据图4无噪声训练组中输入参数为5个的情况,当隐藏层个数在1~4时,RMSE的值都在减小,而在4~10个隐藏层时,RMSE的值存在波动,因此将4~10作为隐藏层个数的备选值。另一方面,随机失活率是一个0~1的概率数字,过大或过小都会反而令测试集的误差升高,尝试将0~0.4作为随机失活率这一维度的备选值,得到的验证组(200个)的RMSE变化曲线如图6所示。
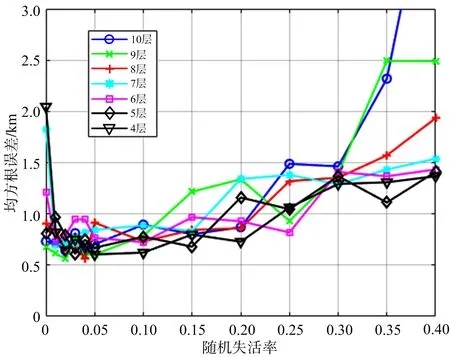
图6 验证组RMSE与Dropout值的关系
从图6可以看出,采用随机失活减少了验证组的RMSE,各曲线的变化趋势为先下降后波动最后上升,图中波动部分的最低处即为最优的参数选择,即当隐藏层数为9层、Dropout值为0.02时,验证组的RMSE数值最小,为0.6 km。
同理,对于有噪声和无噪声情况下不同的参数个数,采用二维搜索,都会得到类似图6的结果,此处不再一一展示,选取图像最低点处作为各自网络模型的最优超参数取值,如表1所示。
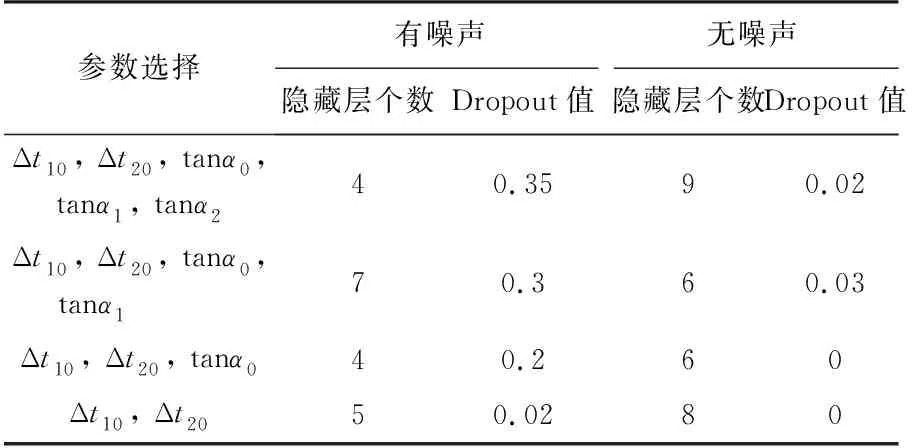
表1 神经网络最优隐藏层数和Dropout值选择
3 仿真分析
3.1 测试组仿真分析
从表1中得到神经网络的最优超参数取值,将有噪声和无噪声测试组的200个样本点分别输入到对应的神经网络中,得到图7中测试组的RMSE图像。从图中可以看出,不管是有噪声组还是无噪声组,随着测量参数个数的增多RMSE值都在降低,证明了神经网络对于多源信息的综合利用。
另外可以计算出在有噪声情况下,测试组的样本点利用1.1节中的方程方法得到的RMSE值为62.03 km。图7显示有噪声测试组中误差的最小和最大值分别为1.52 km和1.65 km,分别对应5个和2个测量参数。
得到结论:使用特定场景下的定位数据训练得到的深度神经网络定位模型,相比于超短基线(如1.2节中雷达间距为1 km)无源雷达定位系统,在此场景下其定位精度可以提高37.70~40.69倍。
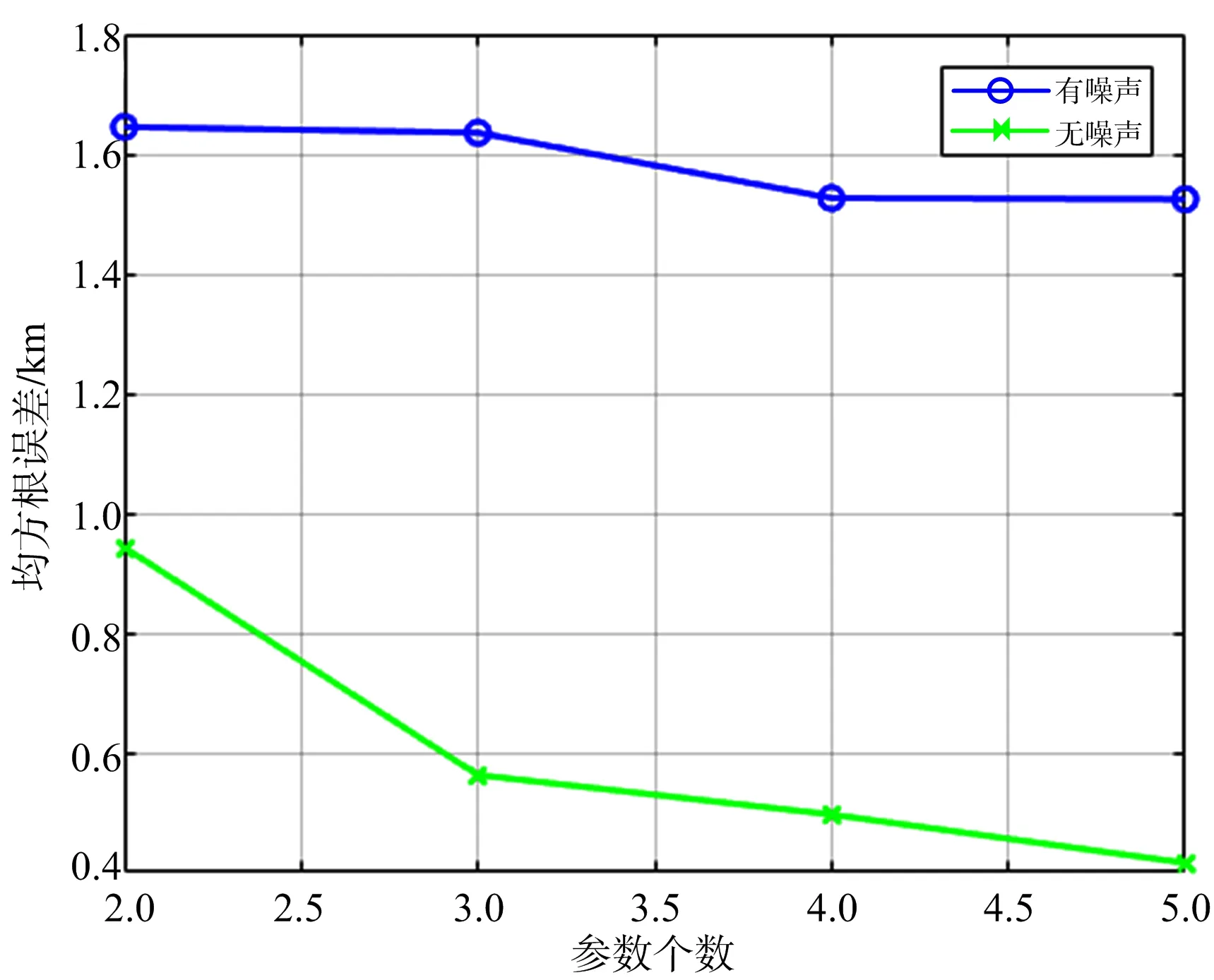
图7 测试组RMSE与参数个数的关系
3.2 对比仿真
分别使用单隐层的全连接神经网络和RBF神经网络对有噪声组样本进行建模,并用测试组样本算出每种方法的RMSE值,最终得到如表2所示的对比结果。
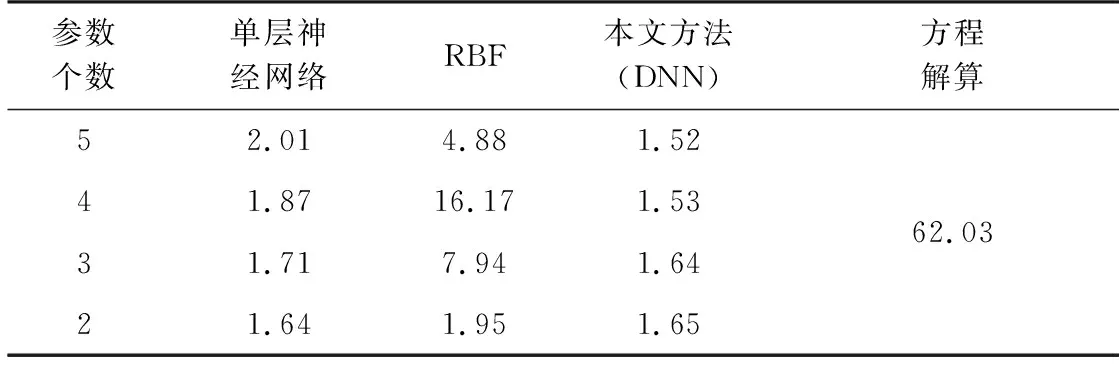
表2 不同方法的RMSE值对比 km
从表2可以看出,浅层的网络结构建模能力有限,在处理大量有噪声的信号样本时,本文提出的深度神经网络模型具有更好的定位精度和多源信息融合能力。
3.3 模型扩展仿真分析
表1中有噪声一栏的超参数组合是用时差噪声均方根为20 ns的样本训练出来的,将这些样本的时差噪声均方根改变,然后输入到此时已经确定超参数的神经网络中,得到如图8和图9所示的结果。
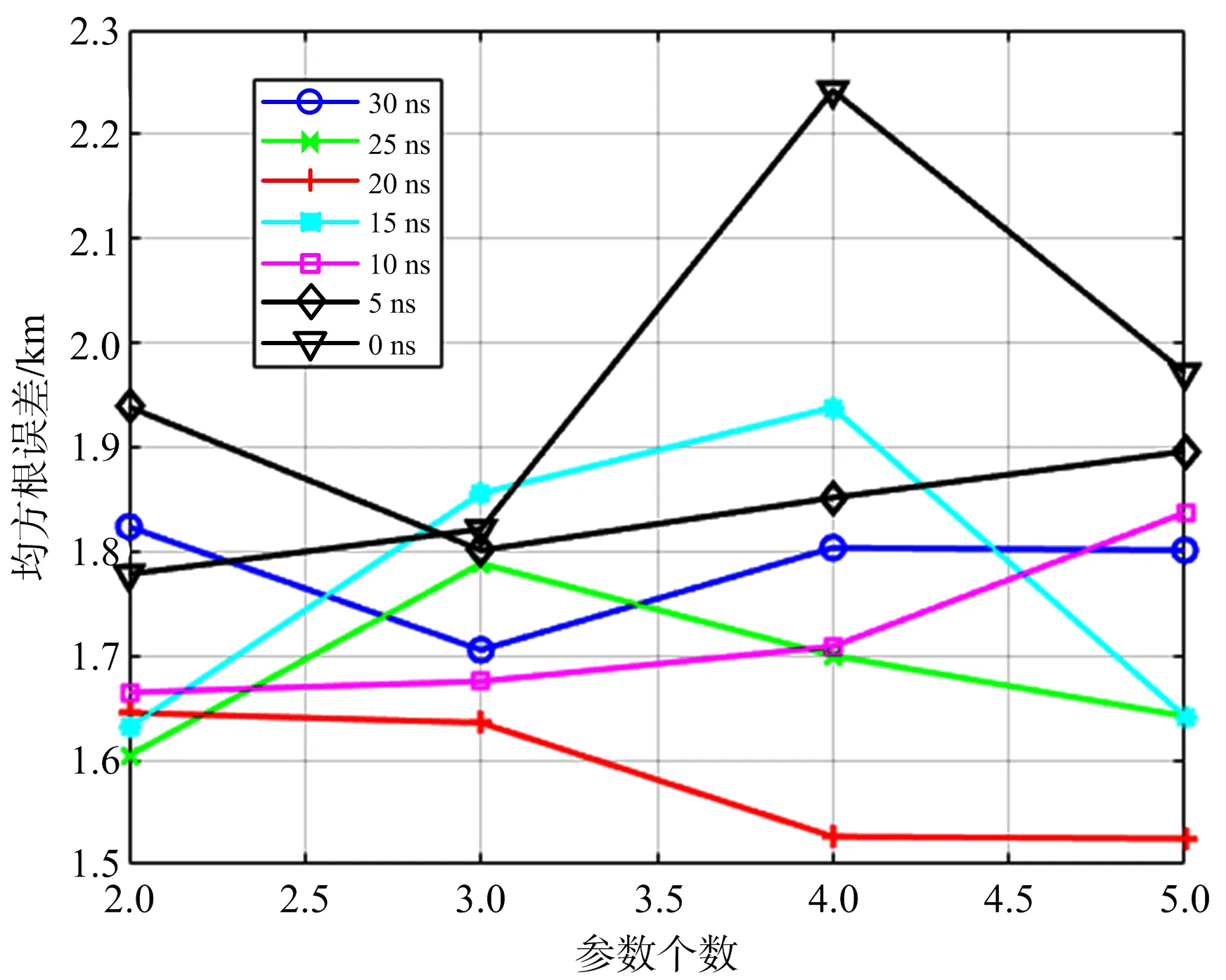
图8 在不同时差噪声均方根取值的情况下RMSE与参数个数的关系
从图8可以看出,虽然神经网络是用噪声均方根为20 ns的样本训练出来的,但也基本适用于不同噪声均方根取值的样本,其RMSE值不超过2.3 km,说明神经网络学习到的不仅是具体的数值,更是对噪声分布的修正。
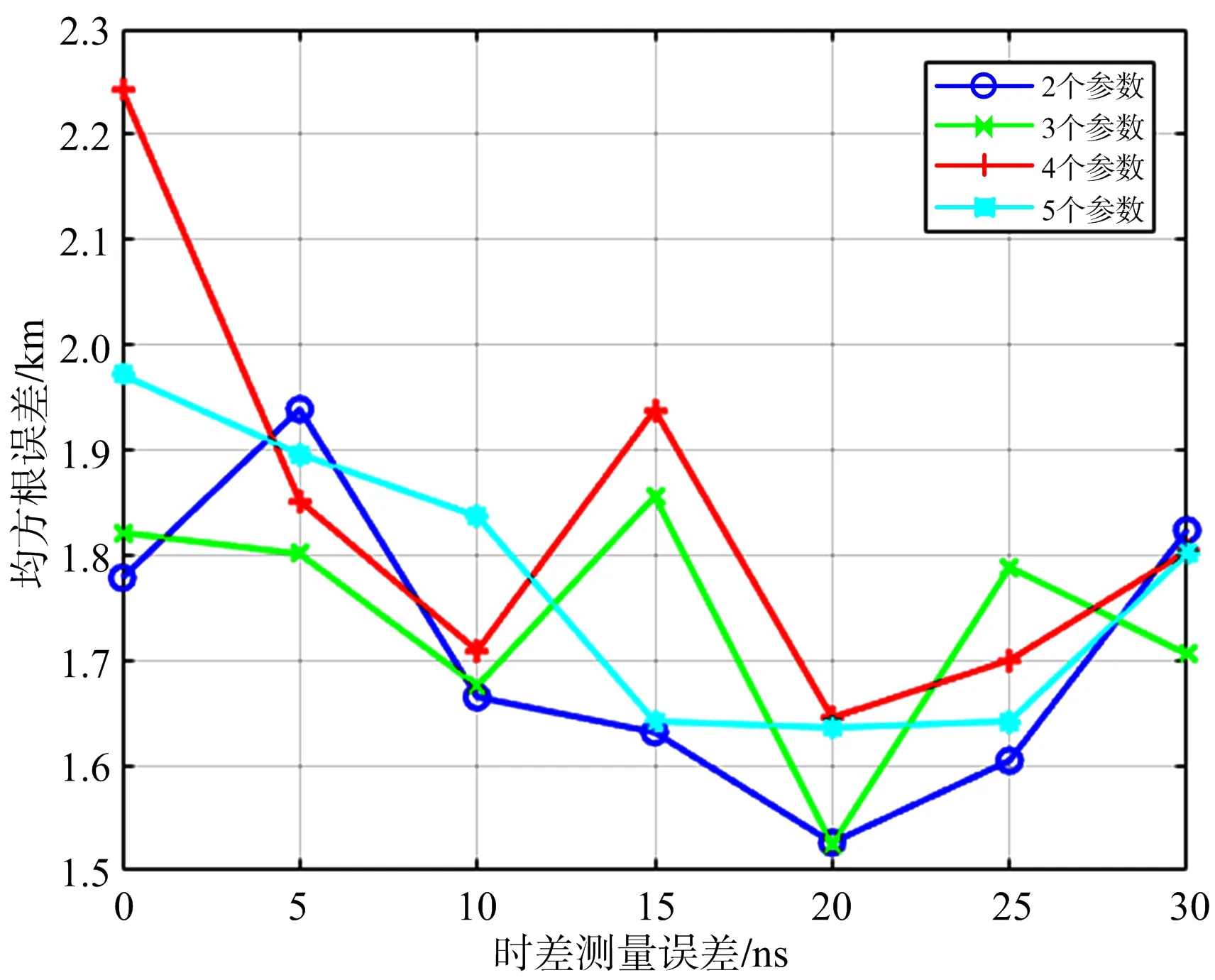
图9 在不同参数个数的情况下RMSE与不同时差噪声均方根取值的关系
从图9可以看出,对于每条曲线,其趋势基本上是从20 ns最低处向两侧进行延伸升高,说明训练数据与测试数据的噪声参数取值越接近,其定位精度越高。
4 结束语
本文提出一种基于深度神经网络的无源定位方法,采用大量样本数据进行经验式学习,以此来替代方程解算这一规则式的定位方法。在离线阶段,通过训练数据和交叉验证数据得到深度神经网络的模型参数。在定位阶段,使用带噪声的不同数量的测量信息进行定位。仿真实验结果表明,该算法可以对多源信息进行综合利用,在噪声统计特性未知的情况下得到更好的定位精度,对特定场景下的超短基线无源雷达定位情况尤其适用。
该方法的主要缺点是需要大量的数据进行训练,误差分布随机性较大,需要和方程定位方法综合使用。

