基于分布式压缩感知的窄带LFMCW旋翼成像方法

, , ,

(空军预警学院, 湖北武汉 430019)

0 引言

直升机旋翼旋转作为微动的一种典型运动[1]，其雷达回波中包含着旋翼图像等信息。研究窄带雷达的直升机旋翼成像方法具有重要的军事价值，因此这一问题引起了众多学者的关注[2-5]。LFMCW雷达具有体积小、重量轻、功耗低等优势，可用于小型预警装备。但“走-停”假设在LFMCW雷达不再适用，必须考虑散射点的脉内运动，因此传统的脉冲式窄带雷达旋翼成像方法不能完全应用至LFMCW雷达中，需要研究针对LFMCW雷达的旋翼成像方法。

目前对于旋翼的成像方法可以主要分为两类，一类是满足方位采样条件[6]的成像方法，如文献[2]中利用基于层析投影算法对旋翼目标进行成像，文献[3]中利用复数后向投影算法对旋翼进行成像，但这些方法在方位欠采样条件下成像会出现虚假点。另一类是不满足采样条件的成像方法，如文献[3,5-6]等方法中，运用到了压缩感知(CS)理论来进行自旋目标成像；这些方法的共同特点是：首先假设转速已知，然后提取出自旋目标所在距离单元的回波，构建相应的稀疏表示模型，最后稀疏重构从而对目标进行成像。当LFMCW雷达脉冲重复频率较低时，会出现方位欠采样的情况，此时采用满足采样条件的传统成像方法会导致成像效果恶化甚至方法失效。而采用如文献[3,5-6]中基于CS理论的方法虽然可以对旋翼进行成像，但这样的方法存在两方面问题：一是如果在信号脉压后使用CS重构散射点，那么当旋翼上散射点线速度过大时，快时间二次项的变化将导致构建的稀疏基不准；二是如果在信号脉压前使用CS重构散射点，那么只能逐一使用单个信号的稀疏特性进行重构，而后将所有信号的重构结果进行叠加，并没有使用信号的联合稀疏特性，从而在某种程度上损失了目标部分信息，导致了虚假点的出现。这些方法大都假设转速已知，而实际中需要估计转速。常见的窄带雷达转速估计方法有时频分析方法[7]、正交匹配追踪算法[7]、高阶矩函数分析法[8-9]、自相关方法[10]等。这些方法存在多普勒频率模糊、计算量大、低信噪比下成像质量变差等问题，其中自相关方法效率较高,具有一定低信噪比条件下的转速估计能力，但是将它用于形状规则的直升机旋翼转速估计时，真实转速与估计转速存在着整数倍误差，该误差倍数等于旋翼对称轴个数。因此，窄带LFMCW雷达直升机旋翼成像方法和转速估计方法有待进一步研究。

针对上述问题，本文结合自相关方法并充分考虑旋翼的形状，首先依据搜索得到的转速估计值对Dechirp后的信号构建联合稀疏表示模型，然后通过分布式压缩感知(DCS)方法进行散射点重构，最后将得到的成像结果分别计算熵值，最小的熵值即对应了最终转速和成像结果。在算法性能上，一方面，由于算法利用了所有距离单元的回波信号以及高阶相位项构建稀疏基，同时利用DCS方法进行重构，因此在低信噪比下具有较好的成像性能；另一方面，由于旋翼对称轴个数是有限的，即最小熵的搜索范围较小，所以本文方法具有较小的计算量。理论分析和仿真结果表明了算法的可行性和有效性。

1 窄带LFMCW雷达旋翼回波建模

直升机叶片模型如图1所示，假设对直升机旋翼回波已经完成平动补偿，此时直升机等效为悬停状态。将雷达、旋翼都投影到一个平面内，雷达到旋翼旋转中心的距离为RC,旋翼上的散射点P到旋翼中心的距离为r，P点到雷达的距离为RP，P点以角速度ω绕C旋转，初始时刻P点的初始旋转角为θ。目标的旋转中心C点位于x轴上，其初始坐标为(xC,0)。选取C为参考点，即Rref=RC。

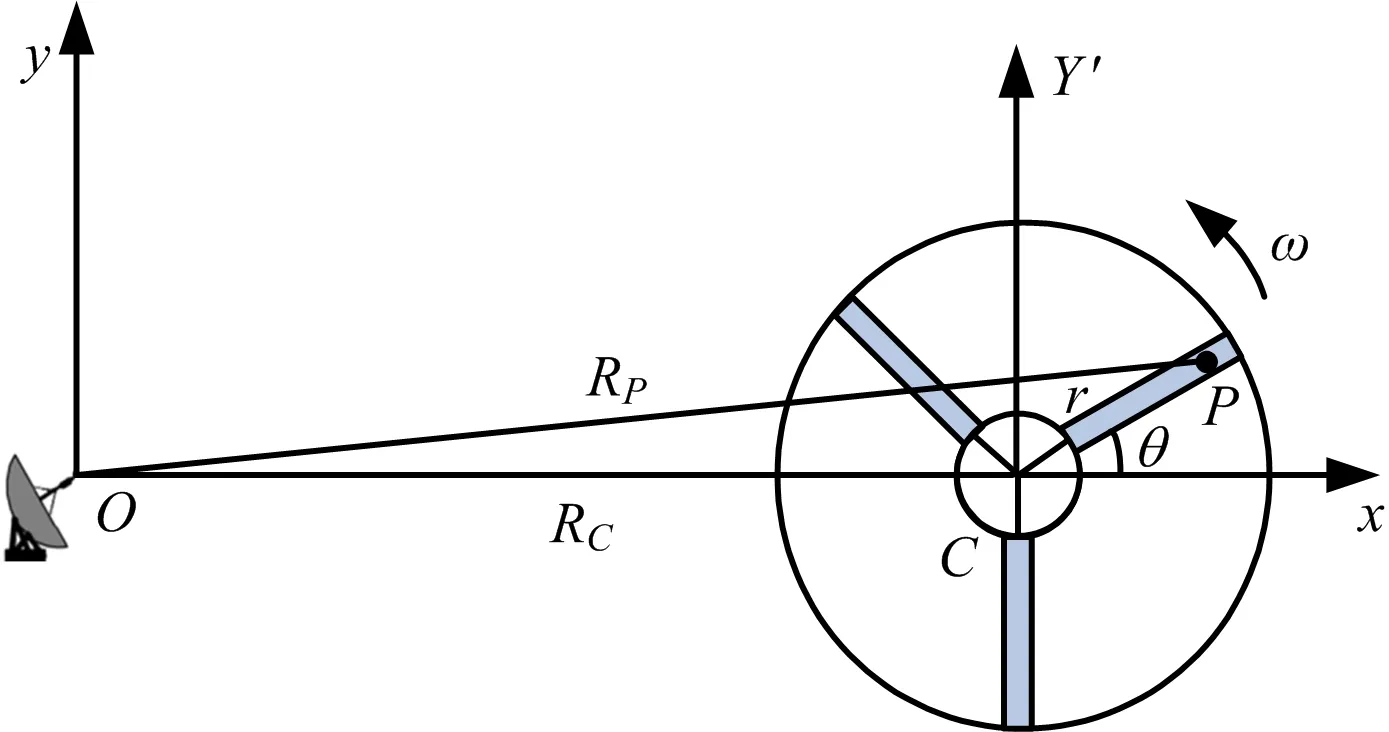
图1 雷达与旋翼关系示意图

雷达发射窄带LFMCW信号，旋翼目标回波[11]为

(1)

参考信号为

(2)

式中，τref为参考时间，τref=2Rref/c。对线性调频连续波Dechirp后的回波[11-12]为

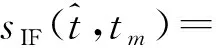
exp[Φ1+Φ2+Φ3+Φ4+Φ5+Φ6]

(3)

现有方法[3,5-6]中，当旋翼转速较低时，Φ5，Φ6可以忽略。因此将式(3)变换至快时间频域，可得到

(4)

式中，RP(tm)=RC+rcos(ωtm+θ)。对于窄带雷达而言，脉压后其回波集中在同一个距离单元内，不会发生越距离单元走动[7]，此时可以利用CS的方法对该距离单元的信号进行散射点重构。

实际上，当旋翼旋转速度较高时，Φ5,Φ6不能忽略，此时式(4)中的相位信息会发生改变。此时稀疏基构建的CS成像方法失效，这是由于快时间二次项的系数是随慢时间变化的，不能得到准确的脉压表达式。因此无法利用CS方法对脉压后的信号进行散射点重构，只能利用式(3)(脉压前的信号)的相位信息进行散射点重构。但这样将带来信号利用不完全的问题，只能逐一通过单个信号的稀疏信息重构散射点，从而导致虚假散射点的产生。本文为了在高速旋转下有效成像，充分考虑信号的联合稀疏信息，建立准确的稀疏基，并结合分布式压缩感知思想进行LFMCW雷达旋翼目标的成像。

2 基于分布式压缩感知的窄带LFMCW雷达旋翼成像

本节首先对LFMCW雷达的旋翼回波联合稀疏性进行分析，并解释可以使用DCS对散射点进行稀疏重构的原因；再依据假设已知的转速信息(实际中转速需要进行估计，本文将在2.3节提出一种估计方法)，构建联合稀疏表示模型，最后利用DSOMP算法对旋翼散射点进行重构。

2.1 联合稀疏性分析

从式(3)可以看出，旋翼的回波信息被分到了每一个快时间点上。对于不同的快时间，式(3)可以改写为

sIF(n,tm)=exp[φ(n,tm)]

(5)

式中:φ(n,tm)=Φ1+Φ2+Φ3+Φ4+Φ5+Φ6；n为快时间的第n个采样点，共有Nr个采样点。式(5)可以进一步表示为

(6)

从式(6)可以看出，该信号可以等效为包含了Nr个散射点距离单元，对于这Nr个散射点距离单元而言，每个信号所携带的信息是相同的，它们都包含了叶片散射点的位置和幅度信息，具有方位向联合稀疏特征。而DCS的思想是利用信号的联合稀疏特性，不是只利用单个信号的稀疏特性对散射点进行重构。相比于CS只利用一个信号的稀疏特性的思想，DCS利用信号联合稀疏特点的思想可以降低散射点错误重构的概率，使得虚假点减少。因此，对于方位向上欠采样的信号利用DCS的思想可以得到完整的成像结果。如图2所示，欠采样矩阵中白色的方格代表有效数据，灰色的代表缺损数据；横轴对应方位向慢时间，纵轴对应距离向快时间。从图中可以看出,不同的快时间点对应着欠采样回波矩阵的一个向量，该向量中包含着散射点的不同的幅度信息和相同的位置信息。而对于这总共Nr个散射点，它们包含的散射点位置信息都是相同的。例如其中某一个信号中包含着某散射点的位置信息，那么其他信号中也应该包含着该散射点的位置信息。通过这个思想，就可以利用信号的联合稀疏性对旋翼进行成像。

图2 联合稀疏模型示意图

2.2 联合稀疏模型建立

首先将目标场景划为维度N×Na的网格，其中在距离向上共有N个单元，在方位向共有Na个单元。式(3)中的ΔR=rcos(ωtm+θ),vr(tm)=rωsin(ωtm+θ)可分别表示为ΔR=xcos(ωtm)-ysin(ωtm)，vr(tm)=ω[xsin(ωtm)+ycos(ωtm)]，其中x=rcosθ,y=rsinθ，x,y是散射点在直角坐标系上的位置。然后对场景进行向量化处理，即令x=vec(X)=[σ1,σ2,…,σK,…]NNa×1，那么对于第n个快时间点而言，其回波的稀疏表示结果[6]为

Sn(m)=Ψn(m,ω)X+e

(7)

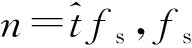
Ψn(m,ω)=exp[A1xkcos(ωmTp)+

A2xksin(ωmTp)]⊗

exp[A3ykcos(ωmTp)+

A4yksin(ωmTp)]

(8)

(9)

式中，X为待重构的图像，||X||2,0为非零行的个数。由式(9)的构建过程可知，该过程与DCS理论相吻合[13]，因此式(9)可视为是一个DCS数学表示模型。典型的DCS重构算法有DSOMP[14]和DSP[15]等，本文采用DSOMP算法进行散射点重构。值得说明的是，重构完成后得到的矩阵维度为NNa×Nr，其中N为快时间的采样点数。将该矩阵的每一列相加得到维度为NNa×1的向量，再将该向量按顺序重新恢复为N×Na的矩阵，该矩阵就是重构的图像。从式(9)可以看出，构建完整的稀疏基首先需要对旋翼转速进行估计，然后再进行DCS重构，即可实现成像。

2.3 基于图像最小熵的旋翼转速估计方法

在本节的成像方法中，转速信息是成像的关键参数，转速估计的精度直接决定了成像的质量。自相关方法具有计算简单、抗噪性能较好等优点，因此可以考虑使用自相关的方法提取直升机旋翼转速[16-17]。首先提取出脉压后目标所在距离单元的信号，然后求取自相关函数，如式(10)所示：

(10)

通过该函数可以求得转速估计值：

(11)

但是，该方法没有考虑直升机的旋翼叶片是对称分布的。而旋翼的叶片数的正确估计有利于旋翼的成像。本文根据直升机的旋翼回波的特点，提出了一种基于窄带LFMCW雷达同时估计旋翼目标叶片数和转速的方法，描述如下。

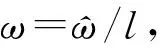
(12)

熵值越小代表图像的聚焦效果越好。综上，直升机旋翼转速和叶片数估计步骤如表1所示。

表1 转速估计算法

综上所述，对应的成像过程算法如图3所示。

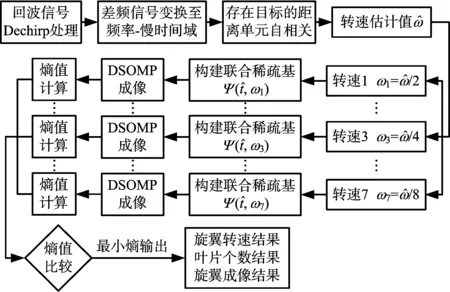
图3 窄带LFMCW雷达成像流程图

本文方法在方位满采样和方位欠采样的条件下均可实现对LFMCW雷达的旋翼目标成像，而这样的效果是其他传统方法所不能达到的，通过第3节的对比仿真可以看出本文算法的优越性。

3 仿真与分析

本文所有实验都是在操作系统为Windows 7的个人计算机上实现的，仿真平台为Matlab R2008b，计算机的主要参数如下：处理器为Intel酷睿E7500，主频为2.93 GHz，内存为2 GB。仿真内容为基于DCS的LFMCW雷达的旋翼成像，直升机距离雷达20 km，转速10π(31.42) rad/s，叶片长度为5 m，形状为四叶片旋翼(对称轴为4个)，直升机旋翼叶片散射点分布如图4所示，散射点之间的距离间隔为1 m。

图4 直升机旋翼模型

本文仿真内容中的噪声为信号脉压后添加的高斯白噪声，信噪比定义为

(13)

3.1 窄带LFMCW旋翼目标回波的时频分布

设置仿真参数如下：发射信号为载频1 GHz、带宽1 MHz、时宽1 ms(重频为1 000 Hz)的LFMCW信号。图5(a)为旋翼在转速为2πrad/s时的时频分布，图5(b)为旋翼在转速为10π rad/s时的时频分布。当自旋速度为2π rad/s时，此时最大的多普勒频率为fdmax=2ωrmax/λ=418.88 Hz，满足采样条件PRF≥2fdmax。当自旋速度为10π时，fdmax=2ωrmax/λ=2 094.4 Hz，不满足采样条件PRF≥2fdmax，此时欠采样倍数为2.09。

图5是对旋翼回波时频分析的结果。通过对比可以发现，在旋翼转速较低时，低重频LFMCW雷达可以通过时频分析的方法对旋翼回波进行时频分析，此时在图5(a)中可以看到有清晰的“正弦”时频曲线；但是在旋翼转速较高时，低重频LFMCW雷达就不能对旋翼回波进行时频分析，此时时频分析方法将会失效；从图5(b)可以看出时频分布图已经模糊，对于传统方法而言，只能对图5(a)中的情况进行旋翼成像，对于图5(b)中的情况算法将失效。本文所提方法不但可以对方位满采样条件下的旋翼目标进行成像，而且可以对图5(b)方位欠采样条件下的LFMCW雷达旋翼进行成像。

(a) 旋翼转速为2π rad/s的时频分布图

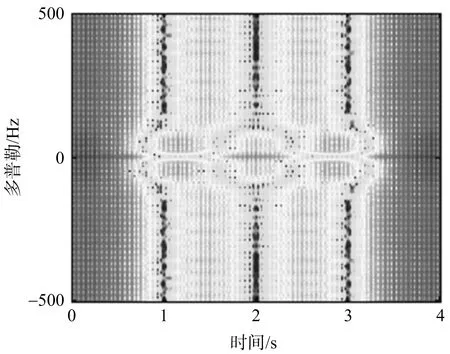
(b) 旋翼转速为10π rad/s的时频分布图图5 旋翼在慢速旋转和快速旋转下的时频分布图

3.2 窄带LFMCW的转速估计

当观测时间为0.5 s时，图6是自相关的结果和图像的熵值曲线。

从图6(a)可以看出，由于旋翼叶片的形状是规则的，此时出现的第二峰值距离中心峰值的时间为0.050 1 s，对应的转速为125.41 rad/s。因此需要使用第2.3节中的方法，基于最小熵原理对旋翼可能的旋转速度进行搜索，计算不同转速下的熵值。如图6(b)所示，当转速为31.45 rad/s时熵值最小，此时对应的转速就是估计的转速。

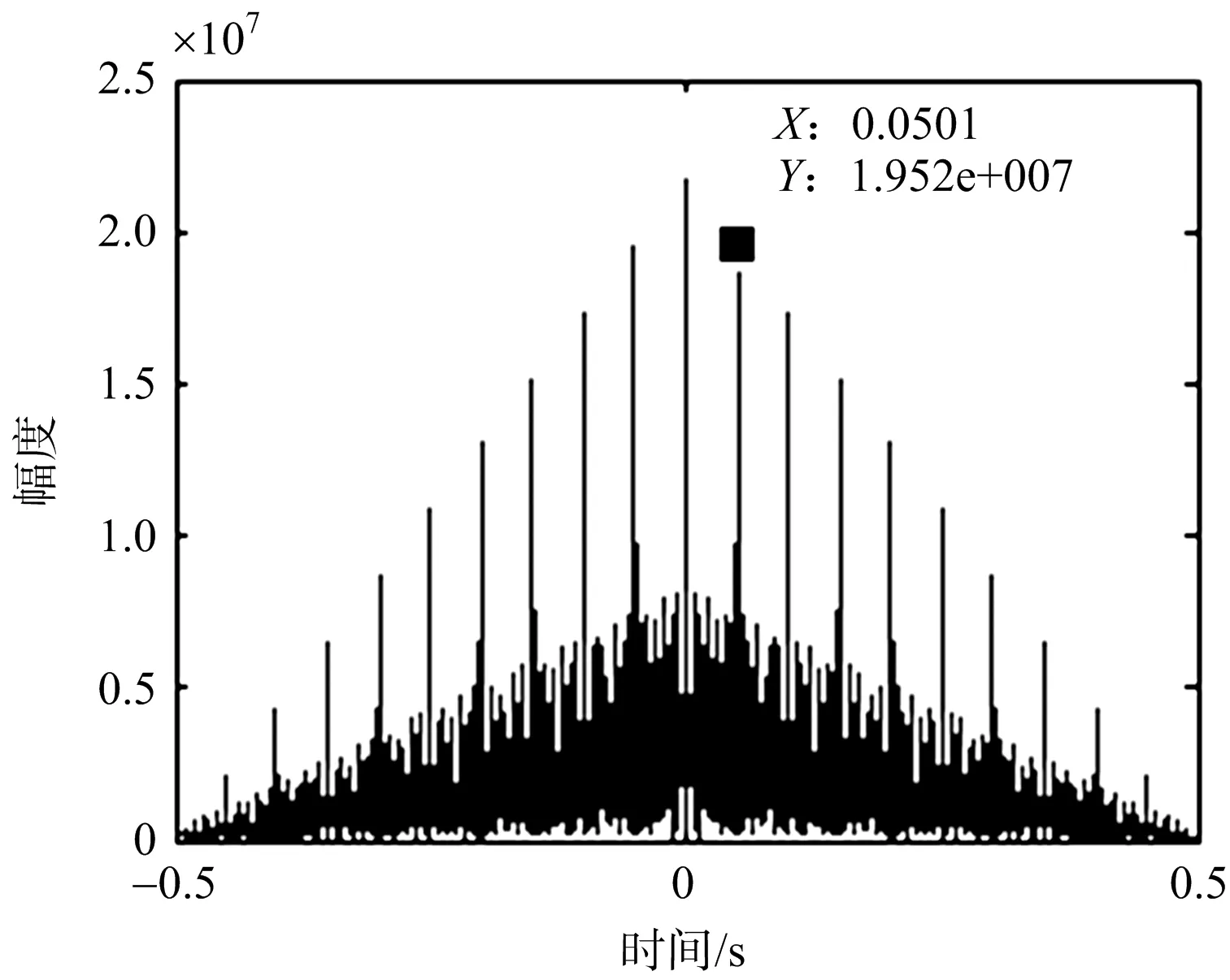
(a) 自相关结果

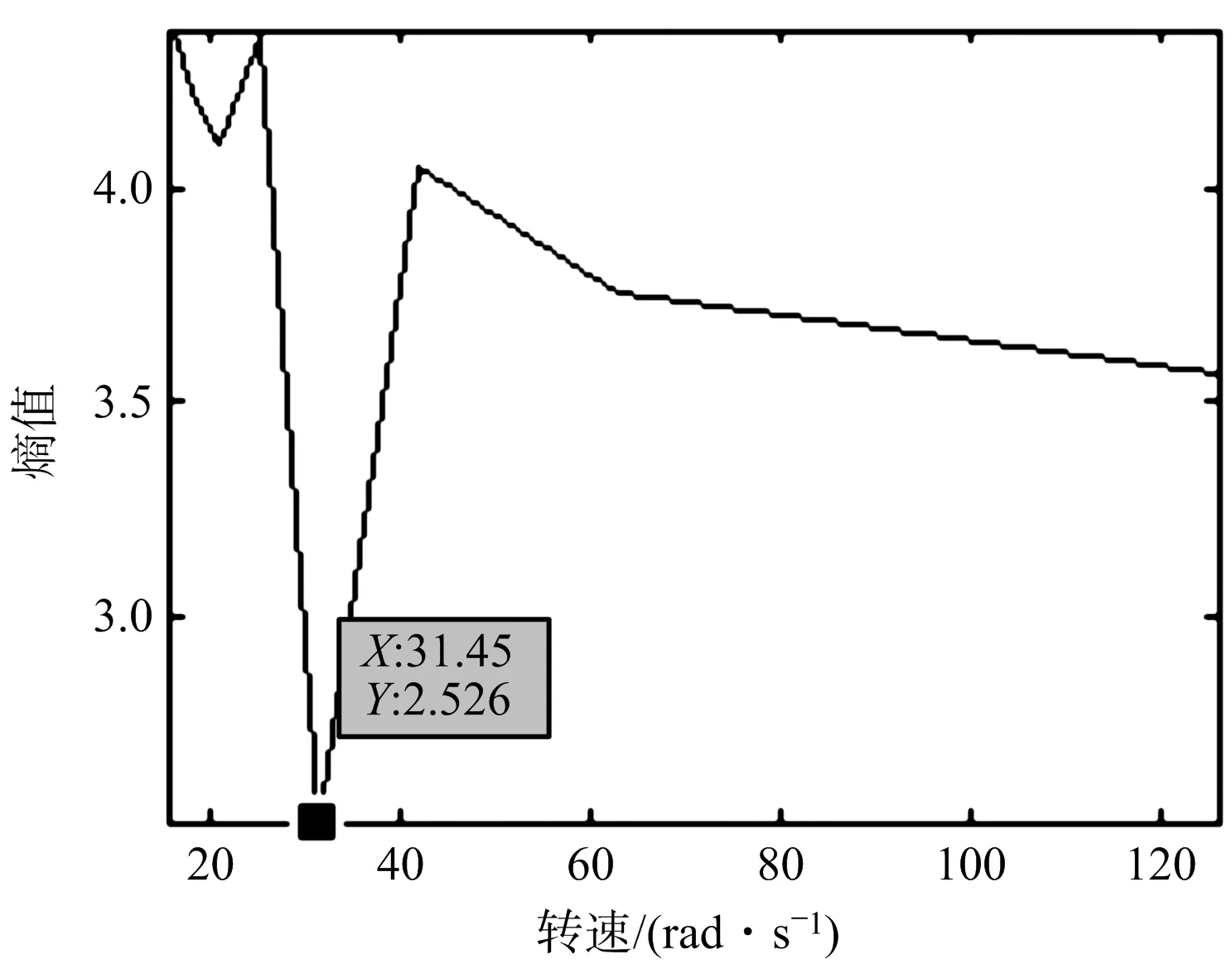
(b) 图像熵值与转速关系曲线图6 转速估计结果

表2分别在估计精度、算法时间、抗噪性能三个方面对比了本文方法、高阶矩函数分析法(方法1)、正交匹配追踪法(方法2)三种算法。需要说明的是，正交匹配追踪算法由于计算量大、所需存储量大，受计算机性能的限制，因此将转速限定在[30 rad/s,40 rad/s]，步长为0.1 rad/s。

表2 转速为31.42 rad/s的直升机旋翼估计方法对比

从表2可以看出，信噪比较高时，3种方法都可以估计出旋翼转速，其中高阶矩函数分析法精度最高，正交匹配追踪算法次之，本文方法最差。但是随着信噪比的降低，高阶矩函数分析法精度变差，可以视为失效，而正交匹配算法和本文方法都较稳定。在运算时间上，高阶矩函数分析方法时间最短，本文方法次之，正交匹配追踪算法最慢。通过对比可以看出，本文方法可以在低性噪比条件下进行较快的转速估计。

3.3 基于DCS的窄带LFMCW直升机旋翼成像

仿真实验的雷达参数与3.1节相同，下面将对比方法1(层析投影算法)、方法2(脉压前CS方法)、方法3(脉压后CS方法)与本文DCS方法分别在低速自旋和高速自旋以及不同信噪比条件下的成像效果。转速为2π时的旋翼成像结果如图7所示。

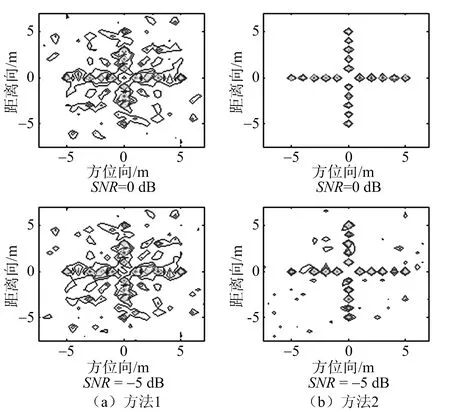
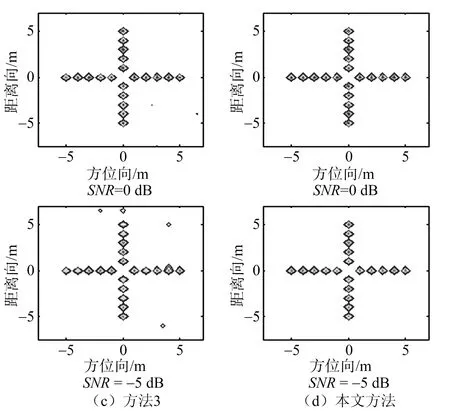
图7 转速为2π时的旋翼成像结果

图7中所有成像结果的熵值如表3所示。

表3 不同算法成像结果对应熵值

转速为10π时的旋翼成像结果如图8所示。

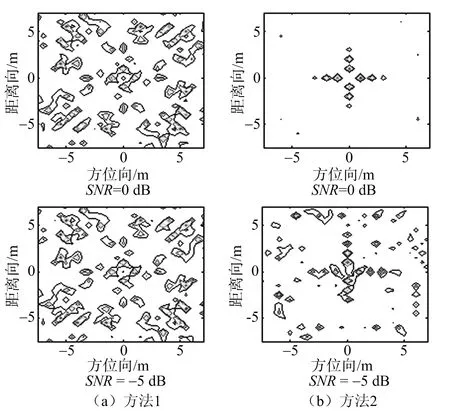
图8 转速为10π时的旋翼成像结果

图8中所有成像结果的熵值如表4所示。

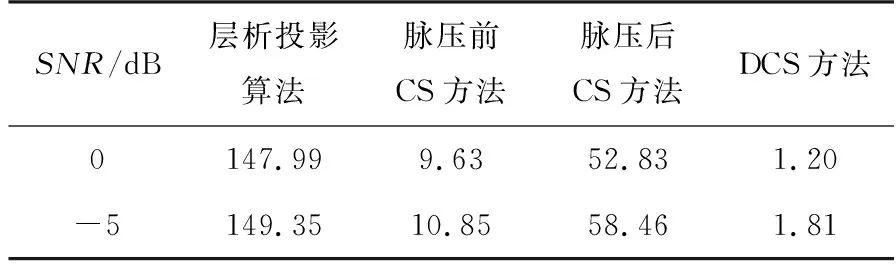
表4 不同算法成像结果对应熵值

从图7可以看出，在转速较低的情况下，4种算法都可以进行成像，但是层析投影算法的成像效果较CS成像效果较差，原因是层析投影算法散射点产生的旁瓣较高，对主瓣产生了影响。从图8可以看出，当转速较大时，方位向上采样已不满足奈奎斯特采样定理，利用层析投影算法已经不能成像。脉压后的信号使用CS方法成像也不能成像，这是因为在较高的转速下构建的稀疏基不准确，不能匹配得到旋翼散射点信息，旋翼边缘上的点已经不能成像。脉压前的信号使用CS算法可以成像，但是由于CS方法只利用了单个信号的稀疏特性，此时重构时会产生一定数量的虚假点以及某些散射点的重构失败。DCS方法利用回波信号的联合稀疏性，恢复出了散射点位置和强度，对旋翼成像质量较好。

4 结束语

本文通过对窄带LFMCW雷达旋翼的回波分析，得到了窄带LFMCW雷达Dechirp后的回波信号。首先将信号脉压并取出包含旋翼的距离单元信号，结合旋翼在形状上是规则的实际情况，通过自相关和基于图像最小熵的搜索方法估计出旋翼转速和叶片个数，通过仿真验证了本文方法具有在较短时间内对低信噪比条件下的旋翼转速和叶片个数估计的能力；然后，本文提出了窄带LFMCW雷达分布式稀疏表示模型，通过对Dechirp后的信号进行所有快时间点的分布式压缩感知，较好解决了常规CS方法中存在的不能完全利用信号稀疏信息、稀疏基构建不准的问题。最后通过仿真验证了该成像方法的有效性。