直升机载ROSAR运动补偿及成像算法
,
(1.中国电子科技集团公司第三十八研究所, 安徽合肥 230088;2.重庆大学飞行器通信与测控中心教育部重点实验室, 重庆 400044)
0 引言
随着我国通用航空快速发展,低空使用逐步开放,低空空域环境日益复杂。能够在低空复杂空域环境和不良气候条件下,对威胁物精确探测和实时感知是保证飞行器尤其是大规模救援情况下多飞行器的安全飞行、提高航空应急救援效率的前提。直升机是迄今为止机动性最优的一种空中平台,可以垂直起降、贴地飞行,可以在未经平整的地点着陆,甚至可以在空中悬停或者占领某一据点。因此,直升机平台是灾区大规模救援和空中作战的理想平台,而目前军民两用直升机的飞行能力主要受限于气候条件。如果缺乏可靠的飞行路径和着陆地点障碍物探测感知手段,在复杂低空空域环境下直升机安全会受到严重威胁。
直升机载旋转式合成孔径雷达(ROSAR)[1-4]天线安装在直升机旋翼叶片的端部或在一个高于旋翼的刚性支架上,利用天线随旋翼的旋转运动来合成方位向孔径,而无需平台的运动,就能够得到对航线周围场景的高分辨图像来实现目标探测和定位。已有的直升机载ROSAR成像算法[2-5]要求在成像过程中平台处于悬停静止状态,然而在实际工作环境中,直升机平台不可能完全处于静止状态,平台的运动将会导致现有的直升机载ROSAR成像算法失效。因此,如何在直升机运动情况下得到聚焦良好的ROSAR成像结果是需要进一步深入研究的问题,这也更符合直升机在飞行和降落过程中感知周围环境的实际需要。
针对上述问题,本文提出一种融合直升机平台运动补偿的改进的Chirp Scaling(CS)算法。本文首先建立了存在平台运动时直升机载ROSAR成像的几何模型,在此基础上,对平台运动引起的目标斜距误差在合成孔径时间内随目标斜距的变化关系进行了详细的分析,得到了平台运动引入的斜距误差的空变特性,并给出了误差补偿方法。然后针对直升机载ROSAR几何构型的特殊性,分析了雷达相位中心等效速度随场景目标斜距变化特性对成像质量影响,并在CS算法的距离徙动空变性校正和方位压缩过程中补偿该影响。所提方法只包含FFT和复乘运算,不涉及插值操作,易于工程实现。理论分析和仿真实验结果表明,该算法能够在直升机平台存在运动时,有效实现对大场景的成像。
1 直升机平台运动的ROSAR信号模型
传统的直升机载ROSAR成像算法针对直升机平台处于悬停静止状态,其观测几何示意图如图1(a)所示。雷达天线安装在旋翼叶片端部,随旋翼叶片的旋转,在地面上形成内径为r1,中心半径为r0,外径为r2的圆环型成像区域,区域大小取决于载机高度H、天线俯仰向波束宽度ε和下视角φ。天线相位中心在z=H的平面内以(0,0,H)点为圆心,旋翼叶片的长度L为半径,作角速度为ω的匀速圆周运动,天线波束指向与旋翼叶片切线方向垂直。
下面考虑直升机运动的情况,假定在成像过程中,直升机平台在z=H平面上沿x轴以速度vx向前运动,如图1(b)所示。令ta为方位时间变量,定义ta=0时刻,天线相位中心位于(L,0,H)。ta=tp时刻,波束中心照射在坐标为(rpcosθp,rpsinθp,0)的点目标P上,其中rp和θp分别是点目标P在XOY平面中对应的半径和与x轴夹角。则ta时刻雷达天线相位中心的位置(xAPC(ta),yAPC(ta),zAPC(ta))可表示为
(1)
式中,θ=ωta是ta时刻旋翼与x轴的夹角。

(a) 直升机悬停情况

(b) 直升机前行运动情况图1 直升机ROSAR成像几何模型
因此,ta时刻点目标P相对雷达天线相位中心的瞬时斜距可表示为
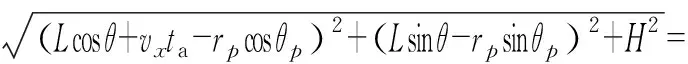
(2)

R(ta)≈
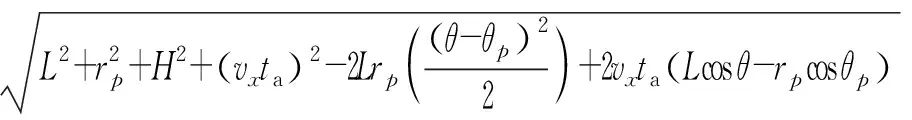
(3)
式中,
(4)

2 直升机平台运动引入的斜距误差影响分析
假设在成像时间内,直升机在z=H的平面上沿x轴匀速向前运动,图2给出了z=H平面上,天线相位中心理想运动轨迹(平台静止)和真实运动轨迹(平台运动)对比,主要仿真参数为:直升机飞行高度为2 000 m,直升机前进速度为50 m/s,螺旋桨旋转角速度为40 rad/s,天线下视角为45°,旋翼叶片的长度为2 m。可以看出,直升机的前向运动导致真实的运动轨迹不是理想的圆弧形,而是呈现螺旋形。因此,在聚焦成像前须补偿直升机运动带来的斜距变化影响,下面从运动补偿的角度分析直升机平台前向运动带来的斜距误差。
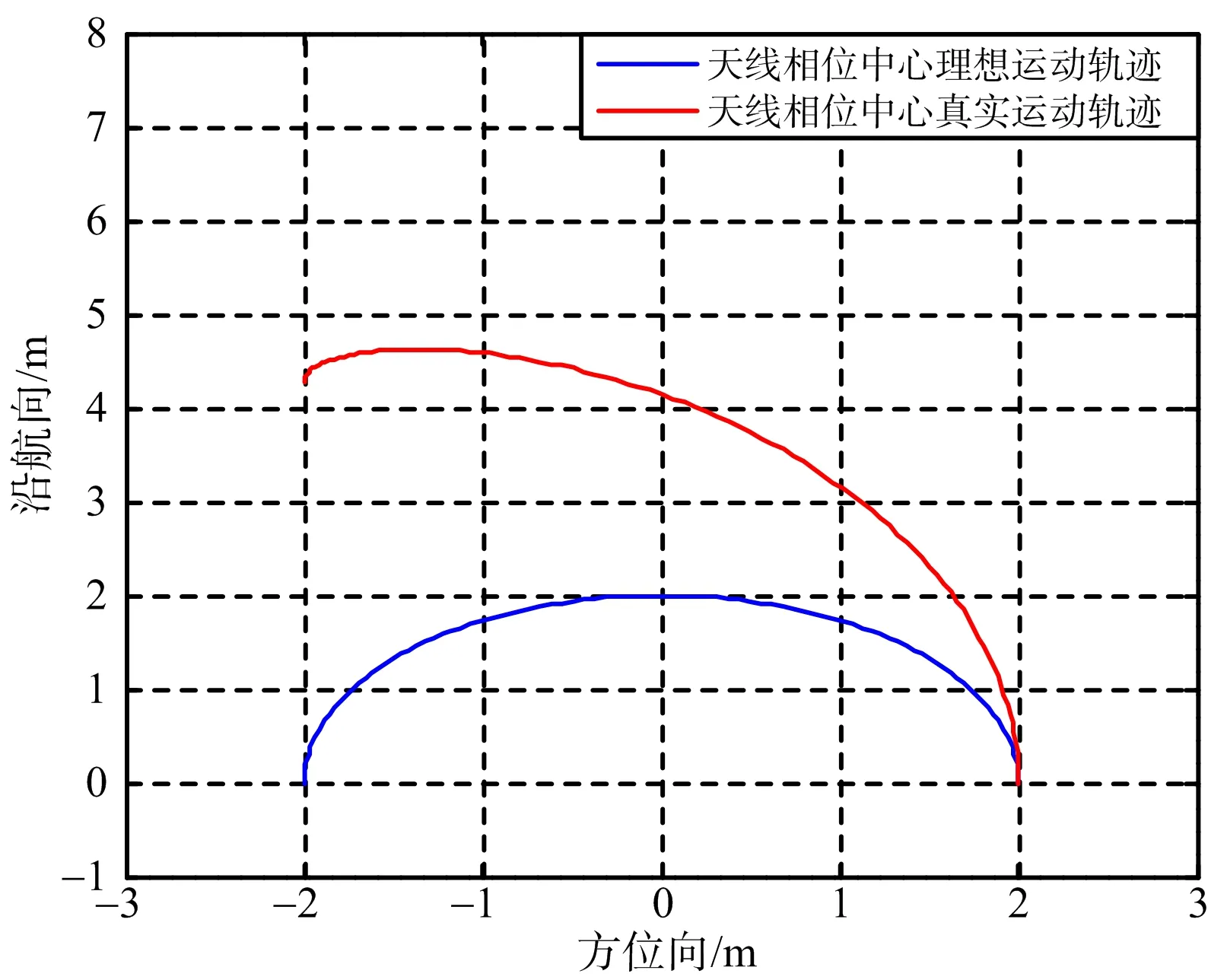
图2 直升机平台运动和静止条件下的天线相位中心轨迹
由式(4)可知,直升机前向运动带来的斜距误差为
(5)
从上式可以看出,该斜距误差与目标在场景中距离和方位位置相关,即该斜距误差具有二维空变性。对场景中任意一个点目标而言,在合成孔径时间边缘时刻ta=Ta/2,斜距变化引起的距离单元徙动和二次相位误差达到最大[6-7],即

(6)
设定成像场景大小为300 m×40°(距离×方位)范围,图3(a)和图3(b)分别给出了在该范围内最大斜距误差随目标距离和方位位置的变化曲线。可以看出,该斜距分量的空变性非常小,因此,在补偿直升机前进运动带来的误差时,可以直接用场景中心对应的校正函数来补偿,而不影响最终的成像质量,从而极大简化补偿算法的复杂性[8]。以此为基础,下节给出存在直升机运动情况下的ROSAR成像处理算法。
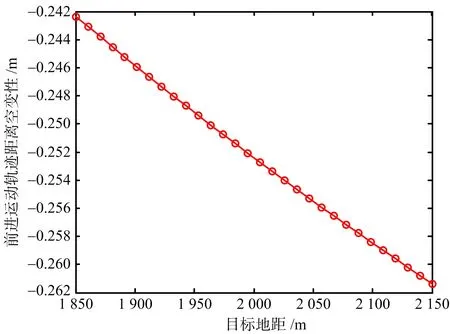
(a) 距离空变性

(b) 方位空变性图3 直升机运动引入的斜距误差空变性分析
3 直升机载ROSAR成像处理方法
本节首先对直升机载ROSAR几何构型所特有的雷达相位中心等效速度随目标斜距变化特性进行了分析,在此基础上,结合运动补偿思想给出了直升机平台运动补偿方法,提出一种适合于直升机平台运动的Chirp Scaling算法。
3.1 雷达相位中心等效速度的距离空变性分析
从式(3)可知,直升机平台静止时的理想斜距表达式为
(7)

假设δθ和δrp分别是相对场景中心位置(θref,rref)的方位和距离偏移量,则该点目标处的斜距和等效速度可写为R(θref+δθ,rref+δrp)和v(θref+δθ,rref+δrp)。在点目标处,速度近似引起的剩余距离单元徙动为
ΔRrcm(δθ,δrp)=|ΔRlrcm(δθ,δrp)|+
|ΔRqrcm(δθ,δrp)|
(8)
式中:ΔRlrcm(δθ,δrp)表示速度近似引起的线性距离徙动量,在直升机载ROSAR信号模型中,由于不存在斜视,ΔRlrcm(δθ,δrp)=0;ΔRqrcm(δθ,δrp)表示剩余二次距离徙动量,在合成孔径时间Ta边缘处的最大,可表示为


(9)
在一定成像区域内,为得到聚集良好的SAR图像,剩余距离单元徙动须满足如下约束:
ΔRrcm(θref,δrpmaxRCM)<γrcmρr
(10)
式中,ρr为距离分辨率,γrcm为常数,一般取1/2,δrpmax为满足式(10)约束的偏离场景中心的最大距离。
同时,二次相位误差须满足如下约束:
(11)
式中,γqpe为常数,一般取1/4,δrpmaxQPE为满足式(11)二次相位误差约束的偏离场景中心的最大距离。
图4(a)和图4(b)分别给出了速度近似引入的剩余距离徙动和二次相位误差随目标地距变化曲线,仿真参数如表1所示。由图4(a)可以看出,速度近似误差引起的剩余距离单元徙动远小于距离分辨率,因此忽略该误差不会影响成像质量[6]。而由图4(b)可以看出,在距离向范围为400 m的成像场景中,大部分区域的二次相位误差超过π/4。因此,在成像过程中,必须补偿速度空变性引起的二次相位误差。

表1 直升机ROSAR系统仿真参数

(a) 剩余距离单元徙动随目标地距变化曲线

(b) 二次相位误差随目标地距变化曲线图4 速度近似引入的误差分析
3.2 改进的Chirp Scaling算法
雷达发射线性调频信号,去载波后的点目标回波信号[6-7]可以表示为
ss(tr,ta)=
(12)
式中,tr表示快时间,c表示光速,λ表示波长,Kr表示调频率,wr(·)和wa(·)分别表示距离窗和方位窗函数。沿快时间进行傅里叶变换,并代入式(3)的斜距表达式,信号的距离频域表达式为
Ss(fr,ta)=
(13)
由第2节分析可知,直升机平台运动引起的斜距误差的二维空变性很小,可以直接用场景中心目标位置对应的误差统一补偿,其补偿函数可写为
(14)
对补偿后的回波信号进行距离向逆傅里叶变换可得
ss1(tr,ta)=
(15)
对上述信号作方位向傅里叶变换至距离-多普勒域完成距离徙动校正,并利用驻定相位原理计算其傅里叶积分,可以得到信号的距离-多普勒域[8]表示式为
sS(tr,fa)=
exp(-j2πfatp)×
(16)

可以看出,距离单元徙动量不仅依赖于方位频率,还与雷达相位中心等效速度有关。由3.1节分析可知,雷达相位中心等效速度随斜距变化引起的距离单元徙动很小,因此,在距离徙动校正时可以忽略其空变性,直接用场景中心目标对应的速度来统一处理,距离-多普勒域的变标函数可写为

(17)
式中,rref为场景中心的地距,Rref为参考斜距,定义为雷达天线到场景中心目标的最短斜距。将式(16)和式(17)的乘积进行距离向傅里叶变换,并根据驻定相位原理计算其傅里叶积分,得到距离徙动校正后的二维频率域[9]表达式为
SS(fr,fa)=σwr(fr)wa(fa)×
(18)
式中:第一个相位项是方位调制项;第二个相位项和第三个相位项是目标方位和距离位置的线性相位;第四个相位项是不随目标距离变化的一致距离单元徙动项;第五个相位项是变标后的距离调制项,可以统一用参考斜距处近似补偿;第六个相位项是变标处理引入的附加相位,它是距离和方位的函数,可以在方位处理时补偿[10]。接着在二维频域进行一致距离徙动校正、距离压缩以及二次距离压缩,完成距离向处理,再作距离向逆傅里叶变换,得到距离-多普勒信号为
sS(tr,fa)=
(19)
相应的方位压缩函数可表示为
HAC(tr,fa)=

(20)
由3.1节分析可知,在方位压缩时,必须补偿等效速度v(rp)随场景中目标斜距的变化,否则会导致目标散焦,相应的变化公式如式(7)所示。完成方位压缩后,再进行方位逆傅里叶变换,得到最终压缩后的目标信号为
(21)
4 仿真实验及其分析
下面通过仿真实验验证所提方法的有效性,仿真参数如表1所示。场景布置如图5所示,9个点目标按方位间隔为20°、距离间隔200 m放置。
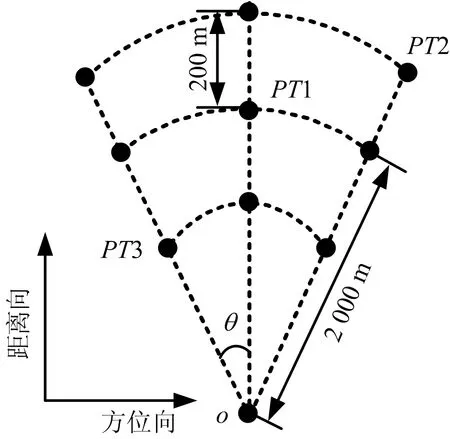
图5 场景点目标分布示意图

(a) 未补偿直升机平台运动的成像结果

(b) 本文方法的成像结果图6 PT1成像结果等高线图
为了方便对比,成像时不作加窗处理。图6~图8给出了场景中心点目标PT1未补偿直升机平台运动的成像结果和采用所提方法的成像结果对比。其中,图6是点目标PT1的等高线图,图7是距离向脉冲响应幅度图,图8是方位向脉冲响应幅度图。可以看出,在未补偿直升机平台运动的情况下,点目标PT1成像结果出现拖尾和散焦,而本文方法同时考虑了直升机平台的运动和特殊几何构型带来天线相位中心等效速度随目标斜距变化的影响,得到了聚焦良好的SAR图像,仿真结果和理论分析一致。类似地,图9~图11给出了场景边缘点目标PT2成像结果对比。图12是整个场景成像结果对比。表2依据分辨率、峰值旁瓣比和积分旁瓣比三个指标,给出了两种方法成像质量评价结果对比。可以看出,本文提出的方法能够得到聚焦良好的直升机载ROSAR成像结果。

(a) 未补偿直升机平台运动的成像结果
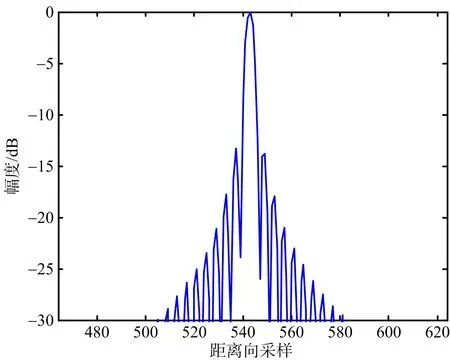
(b) 本文方法的成像结果图7 PT1成像结果距离向剖面图

(a) 未补偿直升机平台运动的成像结果

(b) 本文方法的成像结果图8 PT1成像结果方位向剖面图

(a) 未补偿直升机平台运动的成像结果

(b) 本文方法的成像结果图9 PT2成像结果等高线图
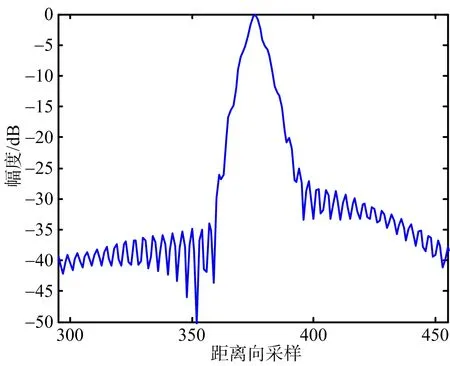
(a) 未补偿直升机平台运动的成像结果
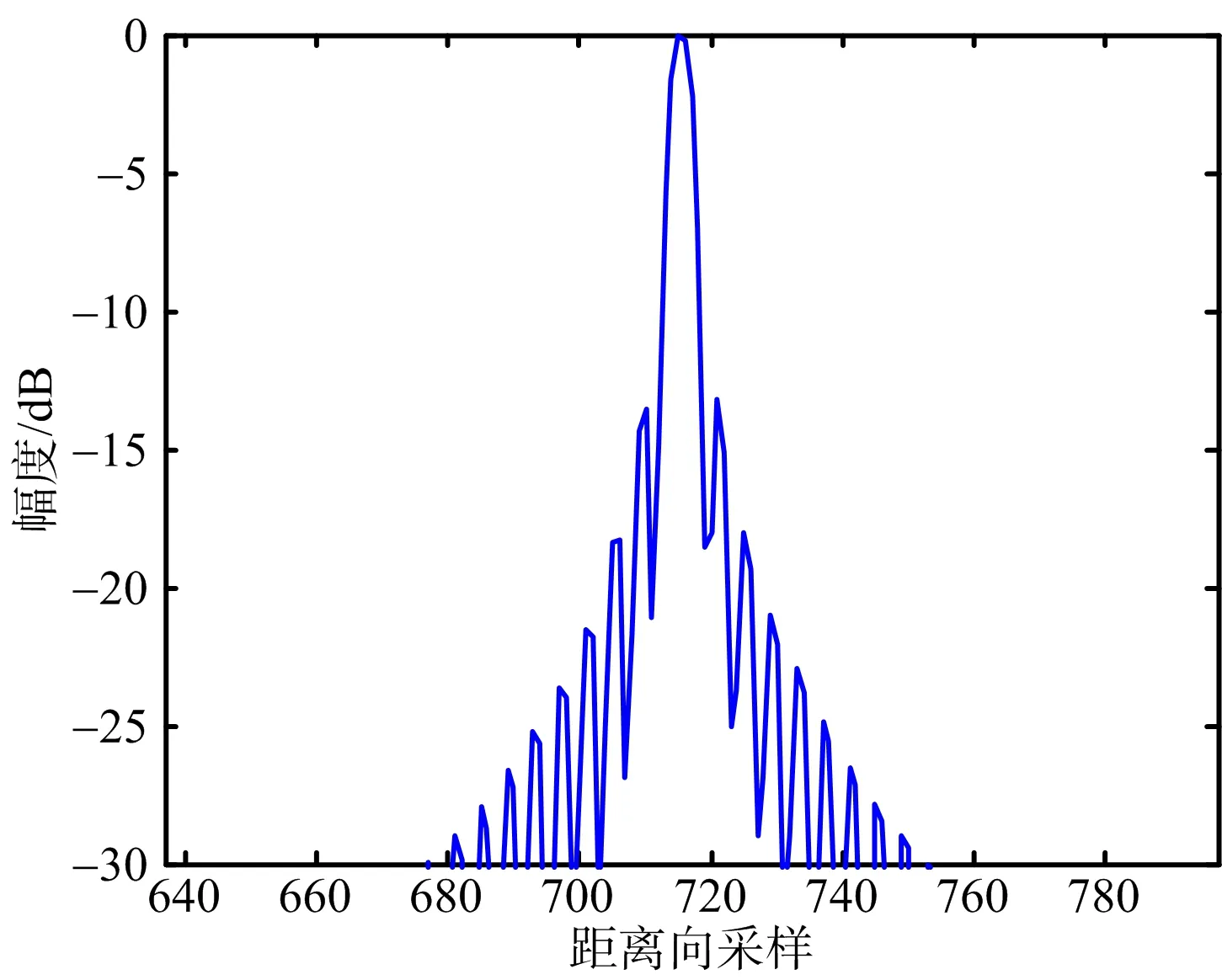
(b) 本文方法的成像结果图10 PT2成像结果距离向剖面图

(a) 未补偿直升机平台运动的成像结果

(b) 本文方法的成像结果图11 PT2成像结果方位向剖面图

(a) 没有直升机平台运动补偿的场景成像结果

(b) 采用提出方法的场景成像结果图12 场景成像结果对比

算法指标PT1PT2PT3传统的CS算法分辨率峰值旁瓣比/dB积分旁瓣比/dB距离向2.176 m2.091 m2.361 m方位向0.857°0.819°0.946°距离向-5.18-6.28-6.17方位向-8.23-7.65-7.14距离向-5.692-7.747-6.526方位向-6.474-6.621-5.791提出的CS算法分辨率峰值旁瓣比/dB积分旁瓣比/dB距离向1.573 m1.520 m1.586 m方位向0.520°0.518°0.521°距离向-13.17-13.22-13.12方位向-13.14-13.20-13.07距离向-9.582-9.629-9.475方位向-9.403-9.582-9.471
5 结束语
本文提出一种适用于直升机平台运动的成像算法。在分析直升机平台运动引起的目标斜距误差空变性的基础上,结合运动补偿思想给出了直升机平台运动补偿方法,并分析了雷达相位中心等效速度随目标斜距变化对成像质量的影响。最后,通过仿真实验验证了理论分析的正确性和算法的有效性。

