基于函数动态递减因子的布谷鸟算法
罗 东,王晓东,段博文
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
布谷鸟搜索(CS)算法是由杨新社等通过模拟某些种类布谷鸟的繁衍寄生行为而提出的一种新颖的智能优化算法,可用来解决最优化问题[1].该算法因具备所需参数少,前期收敛速度快,易实现等优点而被广泛应用.但CS算法存在后期收敛速度慢,求解精度差等问题.为此,众多学者对CS算法进行了优化和改进研究.例如:王凡等[2]提出在鸟窝位置处引入高斯扰动,增加解的多样性,提高原始算法的收敛速度.文献[3-4]将模拟退火思想引入CS算法,增强了算法跳出局部最优解的能力,同时也提高了算法的收敛速度.文献[5-6]利用PSO算法来优化CS算法,将PSO算法用于CS算法的位置更新过程中,有效地提高了求解的精度和稳定性.文献[7-9]利用混沌原理来改进CS算法,使其增加了种群的多样性,提高了搜寻精度和搜寻速度.在步长改进方面已有很多有效的方法,例如:Valian等[10]利用自适应改变步长因子的方法提高了算法的收敛速度.任璐等[11]提出了一种基于逐维改进的自适应步长布谷鸟搜索算法,得到了较好的搜索效果.李荣雨等[12]利用动态惯性权重和记忆策略改进步长,既加快了算法的收敛速度,又提高了算法的稳定性.林要华等[13]将贝塔分布引入步长中,动态调整步长,取得了很好的成果.文献[14]将解的适应度引入到发现概率中,有效地提高了解的质量. 彭建新等[15]提出了一种基于适应值分配的改进步长和发现概率的布谷鸟搜索算法,大幅度地提高了算法精度和收敛速度.在前人研究的基础上,本文根据CS算法不同搜索阶段,在步长和发现概率中引入余弦函数和指数函数,自适应地对步长和发现概率进行调整,以提高CS算法的收敛速度和求解精度.
1 改进布谷鸟搜索算法
1.1 布谷鸟搜索算法
在布谷鸟搜索算法中,通过Lévy飞行对鸟窝进行更新,位置更新公式如下:
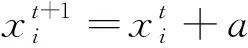
(1)
杨新社教授等人将步长a取为
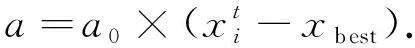
(2)
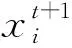
1.2 动态飞行步长
原布谷鸟算法中的a0=0.01,以一个定常数去限定步长a的变化范围,由于算法在搜索前期大步长可以增强搜寻能力,在搜索后期小步长可以提高最优解的精度,因此考虑在a0中引入余弦函数,使其随着迭代次数的增加在区间[0,1]上动态曲线递减,文中设定最大迭代次数为500次,故a0改进如下:
a0=0.001×tmax×cos(t/tmax).
(3)
原始CS算法中的a0恒等于0.01,本文将a0利用式(3)进行替换,然后代入式(1)中,得到改进后的自适应Lévy飞行步长公式,即
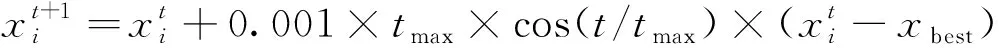
(4)
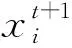
1.3 动态发现概率
原始CS算法中的发现概率恒为0.25,而实际上不同的布谷鸟的发现概率应有所不同,因此发现概率用一个变量去描述更为合理.在算法的搜寻前期,为了增加解的多样性,将发现概率调整得大些,在算法的搜寻后期,减小发现概率,以便减少迭代次数.因此将发现概率改进为
pat=exp(t/tmax)×cos(t/tmax)×pab.
(5)
式中:pat为第t次迭代的发现概率,exp(t/tmax)×cos(t/tmax)为函数动态递减因子,初始发现概率pab=0.4.ICS算法步骤为:
Step 1 设定算法参数:鸟窝数量m,维数n,最大迭代次数,搜寻上下界,初始化鸟窝位置并计算所有鸟窝位置的适应度.
Step 2 对每个鸟窝采用动态调整步长的Lévy飞行(式(4)),产生新的鸟窝.
Step 3 将新鸟窝的适应度与旧鸟窝适应度作比较,保留适应度更好的鸟窝.
Step 4 按照动态调整的发现概率去随机淘汰部分解(式(5)),然后进入随机偏好游动过程,产生新解来代替被淘汰的解,并保留最好的一组鸟窝位置.
Step 5 判断Step 4中最好的位置是否满足算法终止条件,若满足则输出全局最优鸟窝位置和适应度值,否则进入Step 2中继续搜寻最优解.
2 仿真实验
为了检验改进后的布谷鸟搜索算法的性能,采用3个常用的测试函数对基本布谷鸟搜索算法和改进后的布谷鸟搜索算法进行对比实验.设置鸟窝数量m=25,最大迭代次数为500,ICS算法和CS算法均独立运行100次,测试函数见表1.图1~3为测试函数最优值变化趋势图,表2为测试函数最优解位置以及两种算法的搜寻结果,表3为两种算法搜索到的最优值情况.

表 1 测试函数
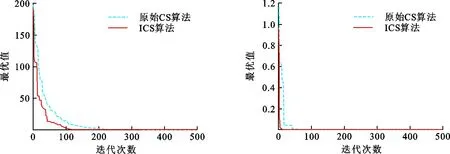
图 1 Sphere函数最优值变化趋势图 图 2 Beale函数最优值变化趋势图 Fig.1 Diagram of the optimal value Fig.2 Diagram of the optimal value change of Sphere function change of Beale function
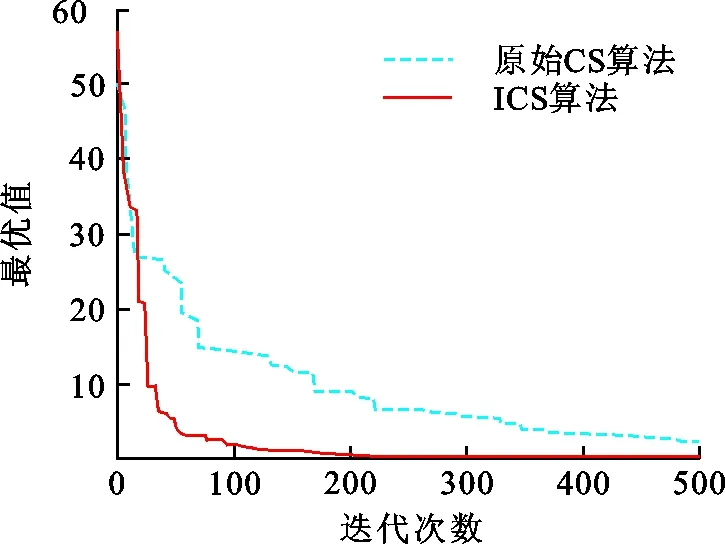
图 3 Lévy函数最优值变化趋势图Fig.3 Diagram of the optimal value change of Lévy function
对图1进行观察,发现ICS算法在迭代初期就出现拐点,比CS算法出现拐点更早,说明ICS算法比CS算法提前进入局部最优,随着迭代次数的增加,两种算法均出现了多次拐点,然后跳出了局部最优,但ICS算法在第120次迭代时收敛到最优值0,CS算法则在迭代240次收敛到最优值0,这说明了ICS算法率先达到最优值. 从图2可以看出,两种算法在迭代前期收敛速度很快,ICS算法在第10次迭代就出现了拐点,CS算法在第15次迭代出现拐点,然后二者跳出局部最优,但是可以看出ICS算法比CS算法更早收敛到最优值0. 从图3可以看出,对于Lévy函数来说,ICS算法在第20次出现拐点,然后迅速收敛,CS算法在第25次迭代出现拐点,二者在后期迭代过程中均出现多次拐点,但ICS算法在迭代220次收敛于最优值0,而CS算法在500次迭代时仍没有收敛,这说明改进后的算法收敛速度有较大改善.图1~3说明ICS算法比CS算法拥有更快的收敛速度,具有更强大的全局搜寻能力.
在n=30的条件下,通过搜寻Sphere函数、Beale函数及Lévy函数最优值位置来测试ICS算法和CS算法的精度,测试结果如下:
Sphere函数:测试函数最优值位置:(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0).
CS算法搜寻的最优值位置:(0.028 9,-0.014 8,-0.020 7,0.017 8,0.029 4,0.008 3,-0.014 9,-0.000 9,-0.015 1,0.037 5,0.019 9,0.001 4,0.001 1,0.010 8,0.016 2,-0.037 4,0.013 7,-0.004 3,0.008 5,0.023 4,0.004 5,-0.000 2,0.011 6,0.011 9,0.008 7,0.009 1,0.030 0,-0.006 9,0.002 8,0.011 4).
ICS算法搜寻的最优值位置:(0.000 2,0.000 3,-0.000 4,0.000 6,0.000 2,-0.000 3,-0.000 5,-0.001 0,-0.000 0,0.000 1,-0.000 7,0.000 7,-0.000 9,0.000 4,0.000 5,0.000 3,-0.000 1,0.000 5,-0.000 2,0.000 3,0.000 3,0.000 5,-0.000 0,-0.000 3,0.000 1,-0.000 4,0.000 3,0.000 5,0.000 5,0.000 3).
Beale函数:测试函数最优值位置为(3,0.5).
CS算法搜寻的最优值位置:(3,0.5).
ICS算法搜寻的最优值位置:(3,0.5).
Lévy函数:测试函数最优值位置:(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1).
CS算法搜寻的最优值位置:(0.935 4,0.996 3,-0.142 5,0.907 7,0.854 8,0.828 0,0.798 0,0.680 3,-0.257 7,1.151 9,1.220 4,0.915 3,-0.199 0,0.662 1,-0.187 0,-0.174 9,-0.183 2,0.993 1,1.146 3,-0.262 2,0.497 6,-0.189 0,1.014 5,1.114 1,0.890 4,0.653 4,0.123 3,0.788 2,1.091 6,1.002 2).
ICS算法搜寻的最优值位置:(1.003 1,0.999 9,0.998 8,0.998 4,1.000 4,0.999 9,0.999 3,0.993 4,0.994 7,0.994 4,0.997 2,1.000 4,1.005 7,0.995 3,1.002 9,0.994 8,1.000 1,0.998 8,1.006 9,0.997 8,1.000 1,1.000 5,0.990 2,0.997 8, 0.997 7, 0.995 8,0.998 1,1.004 7,1.000 8,0.999 1).
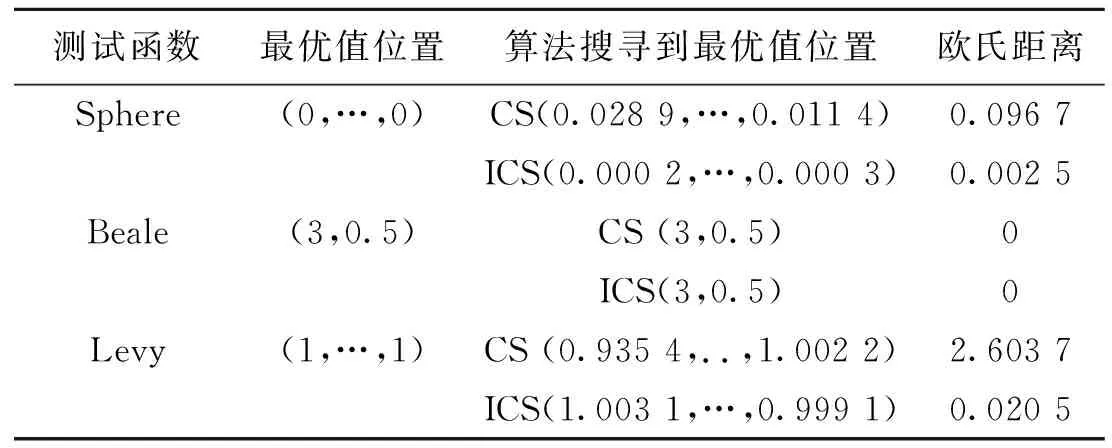
表 2 测试函数最优解位置以及两种算法搜寻结果对比
因为最优值位置处坐标中数字过多,表2中算法搜寻到最优值位置处省略其中间部分数字.
欧氏距离表示CS算法和ICS算法搜寻的最优值位置与测试函数最优值位置的距离.对于Sphere函数,由于 0.096 7>0.002 5,这说明ICS算法搜寻的最优值位置更加接近测试函数最优值位置. 对于Beale函数,CS算法和ICS算法搜寻的最优值位置与函数最优值相同.对于Lévy函数,由于2.603 7>0.020 5,这说明ICS算法比CS算法搜寻到的最优值位置更精确. 所以ICS算法比CS算法在搜寻精度方面有很大提升.
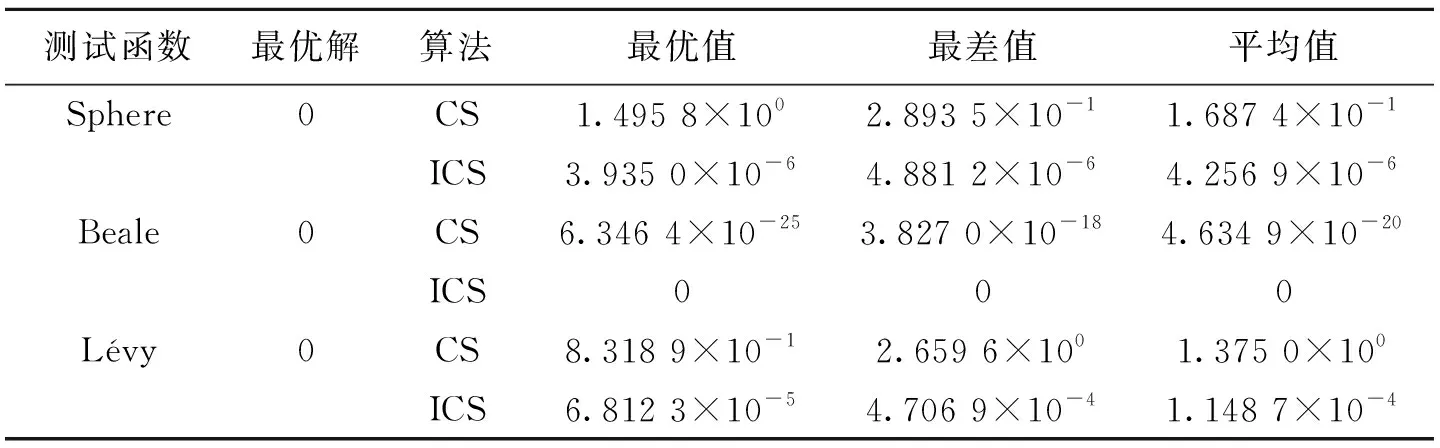
表 3 两种算法搜索到的最优值情况
在表3中,最优值、最差值和平均值分别表示两种算法在独立运行100次后搜索结果中最好的一次、最差的一次和平均值. 由表3可知,对于Sphere函数,ICS算法搜索到的最优值、最差值和平均值均更加接近于测试函数本身的最优值0,这说明ICS算法更加优于CS算法;对于Beale函数,ICS算法搜索到的最优值、最差值和平均值都为0;对于Lévy函数,改进后的算法明显比CS算法更加接近测试函数本身的最优值0,再一次证明了ICS算法优于CS算法.
3 结束语
本文针对步长和发现概率进行了自适应调整,在步长和发现概率中加入余弦函数和指数函数,动态地调整步长和发现概率.利用3种测试函数验证了ICS算法无论在收敛速度还是求解精度方面均优于CS算法.

