有界噪声激励下单势阱碰撞振动系统的混沌运动
刘亚妮,冯进钤
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
现实生活中因摩擦、碰撞等非光滑因素导致的大量复杂现象,使人们对非光滑系统进行了广泛的研究. 冯进钤[1]将光滑系统的多项式逼近、Melnikov方法及随机平均法等初步推广到非光滑系统中. Bernardo等[2]在其专著中详细分析了几类不同非光滑系统的理论,研究了非光滑系统的不连续映射、不连续分岔及混沌等运动.
碰撞是众多非光滑因素中的一种. 早先,Holmes等[3]通过对弹跳小球的研究,得出振幅达到一定值时Smsale马蹄的存在性,使得碰撞的研究有了新的突破. 罗等[4]研究了确定性线性碰撞振动系统的余维一、余维二分岔以及混沌运动,但没有考虑随机激励情形. 对于随机非线性系统的分岔及混沌运动,文献[5-9]已进行了详细讨论,但没有考虑碰撞振动的情形. 冯等[10-11]研究了随机碰撞振动系统的混沌运动,以及谐和与白噪声激励下非线性单边碰撞振动系统的混沌动力学. 由于随机因素与非主流因素表现形式多样,已有文献讨论的还不够详细.
Melnikov方法是判定混沌运动最成熟的解析方法之一. 早期Melnikov方法和理论主要应用在光滑系统下, Holmes等[12]用 Melnikov 方法研究了可积系统在小扰动情况下的混沌运动. 徐等[13]研究了Melnikov方法在一类非线性振子中的应用. 目前,Melnikov方法已初步用于非光滑系统中和一些特殊随机系统中[14]. 文献[15]讨论了一个小周期扰动下的典型非光滑系统的Melnikov方法及其全局混沌动力学;文献[16]推导出横截异宿点的Melnikov函数并将其应用于Hamilton系统来判断扰动后的轨道变化. 本文主要研究具有平方非线性及随机干扰的碰撞振动系统,利用Melnikov方法推导出该系统产生混沌临界值的必要条件,使得Melnikov方法在碰撞振动系统中的应用更加广泛.
1 单边碰撞振动系统模型及同宿轨
考虑谐和与有界噪声激励下带平方项单边碰撞振动系统,系统方程为
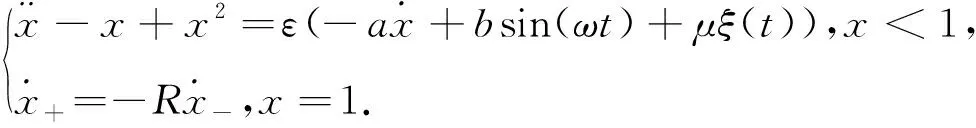
(1)
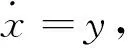
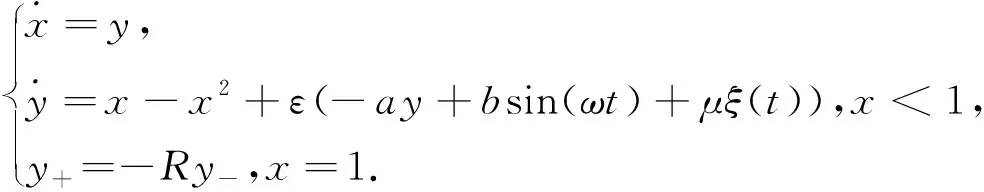
(2)
式中:a为系统的阻尼系数;b为谐和激励的幅值;下标“-”和“+”分别表示碰撞前和碰撞后时刻;R为碰撞恢复系数,满足R=1-εr0;μ为噪声幅值;ξ(t)为有界噪声,用一个含有随机频率与相位的函数来表示,形式如下
ξ(t)=sin(ω2t+σW(t)+V).
(3)
式中:ω2为中心频率,σ为噪声强度,W(t)为单位维纳过程,V为(0,2π)上均匀分布的随机变量.ξ(t)的均值为零,其谱密度函数为

(4)
令系统(2)中ε=0时,得到一个未扰系统
科学家们认为,在橙子、酿酒葡萄和可可等农作物中开展的基因编辑工作能够极大地保护这些植物,未来还能够降低这些农作物对灌溉、化肥和农药的需求。
(5)
由非线性动力学理论易知,未扰系统(5)存在两个不动点S(0,0)和C(1,0),对应的特征方程为
因此,不动点S(0,0)对应的特征值为λ=±1,故不动点S(0,0)是鞍点.C(1,0)对应的特征值为λ=±i,特征根为虚可得出此点是中心. 根据文献[12],得到未扰系统(5)的同宿轨
(6)
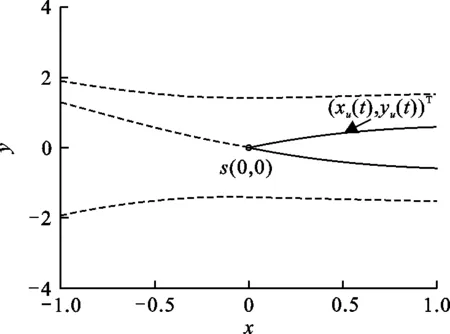
图 1 未扰系统(5)的同宿轨Fig.1 The homoclinic orbits of the unperturbed system(5)

由式(6)可得,未扰系统(5)的相空间图形如图1所示,图1中实线表示同宿轨(xu(t),yu(t))T.
2 Melnikov函数
由Melnikov理论和文献[10,13]知,系统(2)在受到有界噪声扰动下的Melnikov函数为
M(t0)=-aI1-r0I2+bU+μJ.
(7)
其中
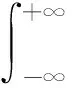
(8)
令式(8)
式(7)中前三项为Melnikov函数的确定性部分,即Md(t0)=-aI1-r0I2+bU,最后一项为Melnikov函数的随机部分,即Mr(t0)=μJ. 利用求有界噪声ξ(t)的方差来观察噪声扰动对均值的偏离程度. 由随机振动理论,随机项Mr(t0)的方差可描述为
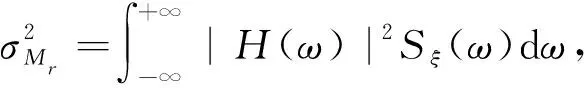
(9)
Sξ(ω)为噪声谱密度,见式(4).H(ω)为频率输入.
故式(9)可化为
(10)
由随机Melnikov理论知,在均方意义下系统鞍点附近稳定流形与不稳流形出现横截相交的条件为
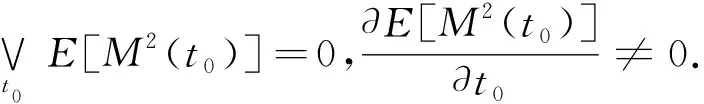
(11)
根据式(11),系统(2)出现Smale马蹄混沌的必要条件为
(12)
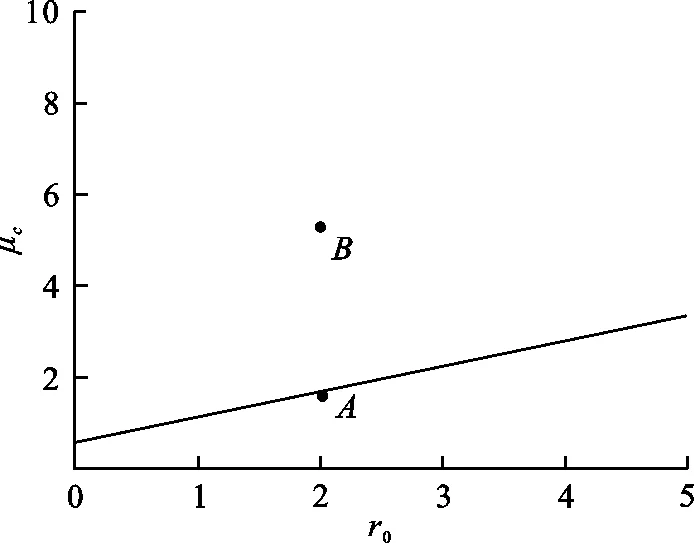
图 2 μc随r0的变化图Fig.2 The threshold value μc for the different values of r0
3 数值仿真
为了验证式(12)中所得结果的正确性,本节将借助数值仿真进行验证. 固定阻尼系数、谐和力幅值、中心频率、噪声强度. 在式(12)中取a=2.6,b=1.8,ω=1.5,ω2=1.5,σ=0.5,由式(12)得到噪声幅值的临界值μc随碰撞参数r0的变化图,见图2.
从图2中可以看出,μc随着r0的增大而增大.因为较大的碰撞参数会导致系统消耗更多的能量.而振子要越过势垒,从一个势阱迁移到另一个势阱,对噪声激励的需求就越大,所以μc随着r0的增大而增大.
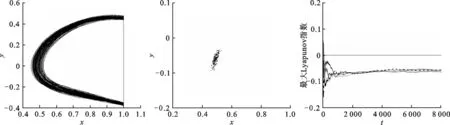
当r0=2.0时临界值μc=1.687,取μ=1.6,如图2中点A,在该条件下做出系统(2)的相图、Poincare截面图和Lyapunov指数序列图,如图3所示. 从图3(a)和(b)可以看出,系统的运动为规则运动,不是混沌运动. 图3(c)为4条样本的最大Lyapunov指数序列图,其最大Lyapunov指数平均值为λ≈-0.08<0,所以该状态下的运动是稳定的,也判断为非混沌态.
(a) 相图 (b) Poincare截面图 (c) 最大Lyapunov指数序列图 3 μ=1.6时系统(2)仿真结果Fig.3 Numerical simulation results of system (2) with μ=1.6
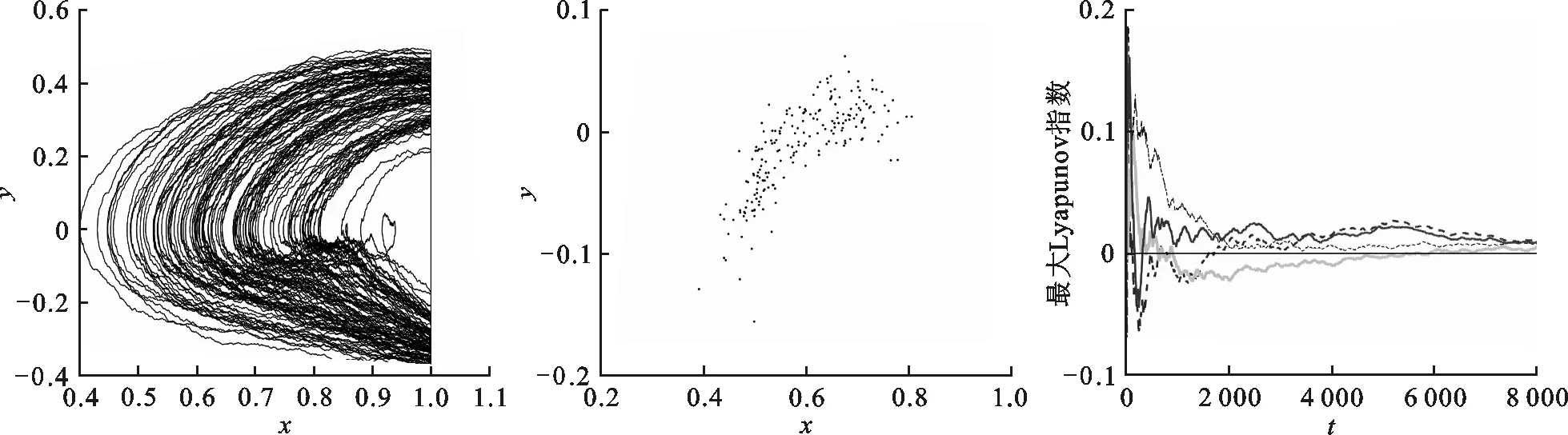
在临界值之上取μ=5.3,如图2中点B,此条件下系统(2)的相图、Poincare截面图和Lyapunov指数序列图如图4所示. 由图4中(a)和(b)可以看出,此条件下系统运动变的混乱. 图4(c)为4条样本的最大Lyapunov指数序列图,得到最大Lyapunov指数平均值为λ≈0.008>0,可判定在此条件下系统的运动状态是混沌的.
(a) 相图 (b) Poincare截面图 (c) 最大Lyapunov指数序列图 4 μ=5.3时系统(2)仿真结果Fig.4 Numerical simulation results of system (2) with μ=5.3
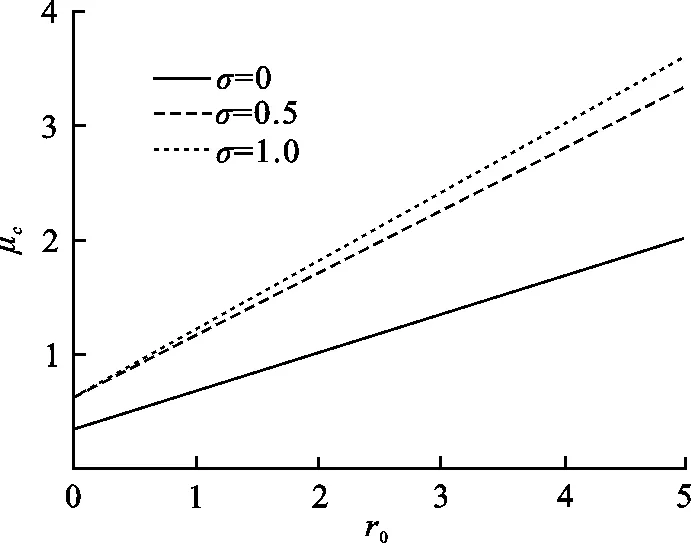
图 5 不同噪声强度下μc随r0的变化图Fig.5 The threshold value μc for the onset of chaos values r0 with different values of σ
当噪声强度σ分别为0,0.5,1时,得到不同情况下噪声激励参数μc随碰撞参数r0的变化图,见图5.从图5可以看出,在r0固定的情况下,μc随σ的增大而增大.这是因为较大的噪声激励需要较大的噪声强度来抑制.同时表明,增大噪声强度可以降低混沌发生的机率.
4 结束语
本文研究谐和与有界噪声激励下的单势阱碰撞振动系统. 运用Melnikov方法推导出系统出现混沌的必要条件,模拟得到的相图和最大Lyapunov指数显示在临界值之下为规则的运动,临界值之上会出现混沌,验证了Melnikov方法的解析结果.研究表明,在一定参数条件下,有界噪声幅值的增大促使混沌运动的产生.而且较大的噪声强度有助于抑制混沌运动.

