4级重复级低速模拟压气机的试验与计算

刘宝杰 ，张 帅 ，于贤君

（1.北京航空航天大学能源与动力工程学院北京100191；2.北京航空航天大学航空发动机气动热力国防重点试验室，北京100191；3.先进航空发动机协同创新中心，北京100191）

0 引言

高压压气机的研制一直是现代航空发动机设计中的关键问题之一[1]。在当前的设计体系下，高性能高压压气机设计很大程度上依赖于对其内部复杂流场的认识，由于受其转速高、叶片相对尺寸小、结构紧凑以及高温高压的环境、昂贵的试验费用等的限制，采用常规方法很难详细测量高压压气机内部流场。这也直接限制了压气机设计体系的发展和完善。

20世纪70年代中后期发展起来的低速模拟试验研究技术，实现了在低速环境下模拟高压压气机后面级高速环境流动，试验成本大大降低，而且便于进行内部流场的详细测量。D.C.Wisler等[2-3]最早在GE公司E3计划支持下，首次提出保持雷诺数、稠度、叶表无量纲速度分布等参数相同的低速模型，建立了4级重复级低速大尺寸压气机试验台并以此为依托发展了定制裁剪叶型和3维造型技术；PW公司[4-5]、NASA[6]以及RR公司联合Cambridge大学和Cranfield大学[7-9]等，也开展了低速模拟技术的研究。低速模拟技术的飞速发展对20世纪七八十年代压气机设计水平的进步提供了关键支持[10]。

国内对于低速模拟试验技术也做了大量工作，北京航空航天大学在20世纪80年代建立了国内首个低速大尺寸压气机试验台[11]，并研发了1整套转子流场动态测试技术；南京航空航天大学在2010年前后，按照GE公司的思路建立了国内首个4级重复级低速大尺寸压气机试验台[12]，并发展了相关的试验测量技术[13]；中科院工程热物理所在近年也进行了低速模拟技术的研究并设计和建造了低速大尺寸压气机试验台[14]；上海交通大学和中国航发沈阳发动机研究所合作开展了高压压气机进口级低速模拟设计的数值分析[15]。国内对于压气机低速模拟技术的发展比国外落后一些，除了需要建立完备的低速模拟技术设计体系外，完善准确的试验测量也迫在眉睫。此外，当前对于压气机设计人员而言，在对设计方案进行最终试验验证前往往通过商用软件校核，但数值模拟软件的可靠性有待商榷，而完整的低速模拟试验数据提供了软件校核的细致数据。

本文在北京航空航天大学新建立的4级重复级低速模拟压气机试验台[16]上搭建了全面的测试系统，对试验台做了细致测量，同时应用试验数据对常用的数值模拟软件进行了校验分析。

1 试验设备及试验方案

1.1 试验设备简介

为了系统地开展4级重复级低速模拟研究，于贤君、刘宝杰等完成了模拟某先进发动机后面级典型流动的气动方案设计[16]的同时，与某研究所共同完成了4级重复级试验台的结构设计、加工和装配以及试验测量。试验台的结构模型如图1所示。试验段结构由导叶和4级几何参数相同的叶片组成，试验叶片加工采用树脂加玻璃纤维强化的方式，试验台（下文简称4Stages）的主要设计参数见表1。

1.2 试验测量方案

本文系统测量了4级重复级压气机的特性、级间气动参数的展向分布以及静子后的流场。试验台的所有测量截面如图2所示。

图1 4级重复级低速模拟压气机结构模型

表1 4级重复级低速模拟压气机主要设计参数

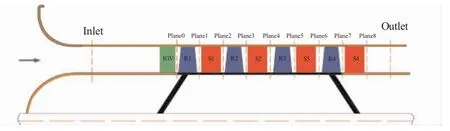
图2 4级重复级测量截面

本文测量的压气机的特性是总压升系数和效率随流量系数的变化曲线，通过调节压气机出口机械阀门的开度来控制压气机的流量状态。为了测量试验台的流量系数，通过在进口Inlet截面均匀布置的4个壁面静压孔测量到的平均静压Ps,in，结合通过振筒气压计和高精度温度传感器测量的压气机进口的大气压强 Pt,in和温度 Tt,in，通过式（1）求得

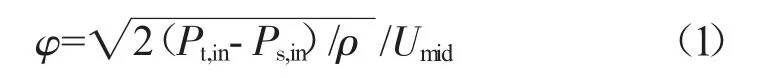
式中：Umid为转子叶中切线速度。

总压升系数定义为

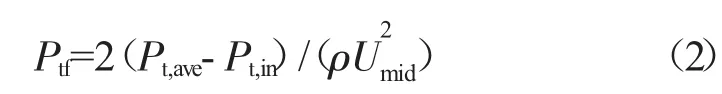
式中：Pt,ave为试验台出口截面的平均总压，通过在出口截面布置的8个总压耙通过面积加权的方式求得。

本文测量的压气机效率为扭矩效率

式中：π为压气机压比；Win为压气机进口物理流量；n为物理转速；k为定比热；R为气体参数；M为扭矩。

本文通过控制位移机构带动5孔气动探针移动到待测点，并设置等待时间，待流场稳定后采集5个孔压力数据，经过数据处理获取级间各截面的气动参数，5孔针数据处理方法见文献[17]。测量用的5孔探针放大照片和转子后测量用的位移机构如图3所示，转子后测点沿径向的布置如图4所示。近机匣第1个测点距离机匣2 mm，近轮毂第1个测点距离轮毂3 mm，主流区域的测点间隔约5%叶高，在叶根和叶尖区域加密，共布置24个测点。

图3 试验用5孔探针放大及转子后测量用位移机构

图4 转子后测点沿径向的布置

静子后的流场测量采用2维位移机构控制5孔探针扫描静子出口扇形截面的方式进行。静子后测量用的位移机构和测量网格如图5所示。测量节点共18×17（306）个，覆盖了1.1倍静子周期，并在尾迹区域和端壁进行加密。与轮毂最近的测点距离为4 mm，与机匣最近的测点距离为2 mm。静子出口气动参数的展向分布通过相同半径的测点数据进行加权得到。

1.3 5孔针重复性测量和精度

为了考察5孔探针测量的重复性，对第2级转子（R2）后的设计状态（流量系数为0.62）和第2级静子（S2）后的堵塞状态（流量系数为0.68）进行重复测量。第2级转子后气流角和流量系数（Vz/Umid）沿展向分布的对比如图6所示。从图中可见，前后2次试验数据具有高度的一致性。

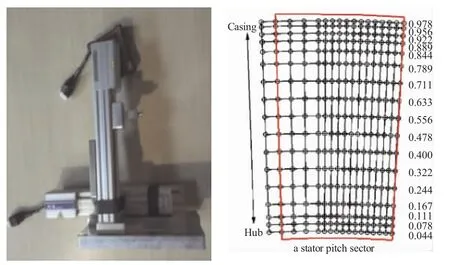
图5 静子后测量用位移机构及测量网格

图6 设计状态下第2级转子展向分布的重复性对比

图7 堵塞状态下第2级静子展向分布的重复性对比

堵塞状态（流量系数为0.68）下第2级静子后气流角和流量系数展向参数以及流场的重复性对比如图7、8所示。从图中可见，静子出口流场周期性良好，流场结构和气动参数展向分布都具有很强的重复性。5孔针测量的精度见表2。

图8 堵塞状态下第2级静子后无量纲轴向速度重复性对比

表2 5孔针测量精度

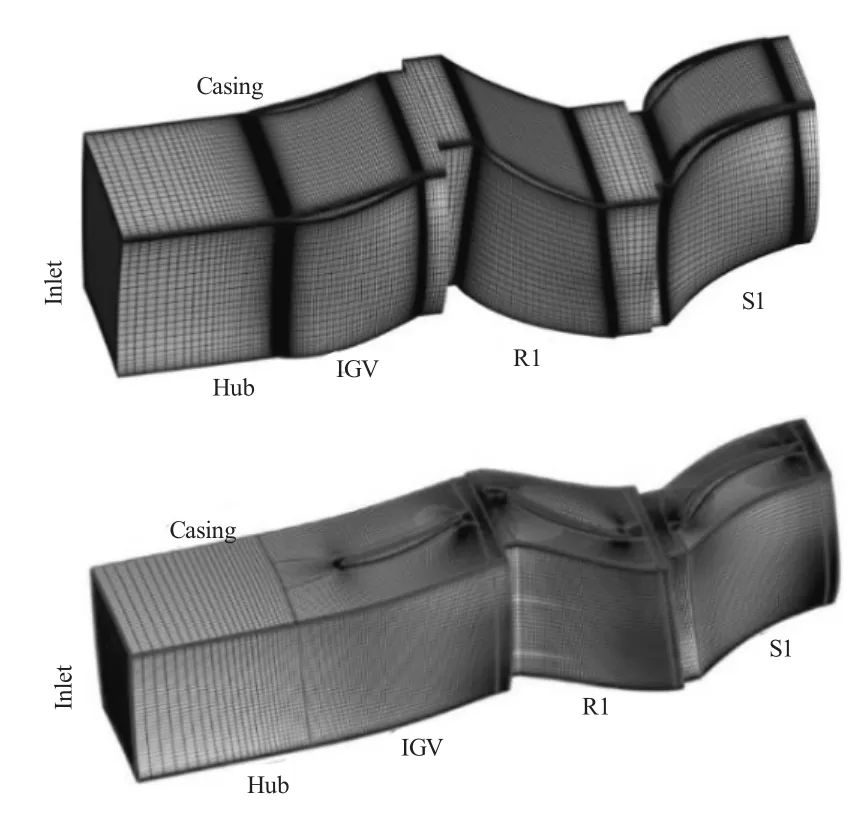
图9 数值模拟采用的计算网格

2 数值模拟方法

当前的设计体系的初步方案校验主要采用3维数值模拟软件。本文利用试验数据校验了3种常用的计算程序：Turbo程序和商用软件CFX、Numeca。

Turbo程序最初由Denton[18]开发，湍流效应通过采用混合长度模型考虑，气体的黏性通过薄剪切层近似模拟，计算程序可以实现在可接受的精度下尽量占用少的计算资源，迅速得到计算结果，从而帮助设计者很快地调整设计方案。本文采用的计算程序是刘宝杰等[19]通过对大量试验结果校验改进的版本TURBO-N7。Turbo采用简单的H型网格，如图9上图所示。这里只给出导叶和第1级网格，因为后面3级网格与第1级网格参数完全一致，IGV网格块在流向、周向和径向分别有175、37和45个节点，Stator和Rotor的网格节点数是138、37和45个，第4级静子的网格节点数为178、37和45个。计算网格总数约217.1万。网格在壁面进行适当加密y+=11左右，以满足湍流模型的计算要求。

CFX与Numeca计算采用同一套网格，如图9的下图所示。使用Autogrid5模块生成，叶片主流通道采用典型的O6H型网格拓扑结构，间隙内采用OH蝶型网格，从而保证网格的正交性，同时在叶片前尾缘、叶片表面、间隙、壁面适当加密，网格的Y+绝大部分控制在1左右，总网格数为767万，保证了对流场特征的捕捉。Numeca计算采用S-A湍流模型，CFX采用kω湍流模型。

3个计算程序的计算求解都是给定了进口的总压、总温和气流角，计算域出口给定的是反压。

3 试验结果分析

3.1 压气机特性

试验测量得到的压气机特性如图10所示。设计点流量系数为0.62，效率为88.7%，总压升系数为3.06，峰值效率约89%，综合裕度为39.04%，这些性能指标对于当前的压气机设计水平来说具有典型性，并且具有较高水平，证明该低速模拟压气机的高压原型同样具有良好的性能指标。本文沿特性线选取4个状态点分别为近堵点（NC）、设计点（DE）、中间状态点（MID）和近失速点（NS），流量系数分别对应0.68、0.62、0.54、0.46，进行级间参数和流场的测量。

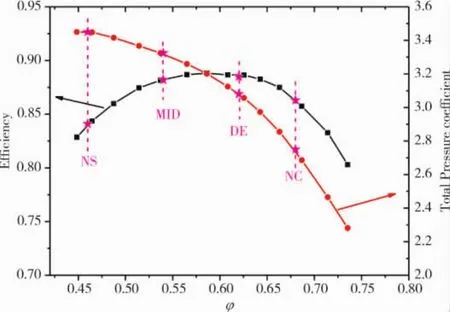
图10 4级重复级试验特性

3.2 展向气动参数分布

各级转子出口流量系数展向分布在4个流动状态下的对比如图11所示。首先在NC和DE流量较大的状态下第1级转子叶尖区域的端壁堵塞较弱，出口流量的展向分布比较均匀，经过第1级的充分发展后端壁的流通能力在第2～4级转子出截面尖部区域基本相似；在MID和NS流量较小的状态下，4级转子出口端壁的流通能力基本相当；在所有工况下，4级转子的根部流通能力逐渐降低。尽管各级转子的流量展向分布有些许差异，但是总体来看，在所有工况下，第2～4级转子出口的流量沿展向的分布非常近似。第2～4级转子的气流折转角（如图12所示）和D因子（如图13所示）的展向分布也是一致的，说明2～4级转子内的流动也基本一致。

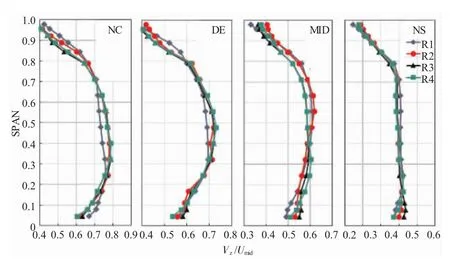
图11 不同流量状态下各级转子出口流量系数展向分布对比

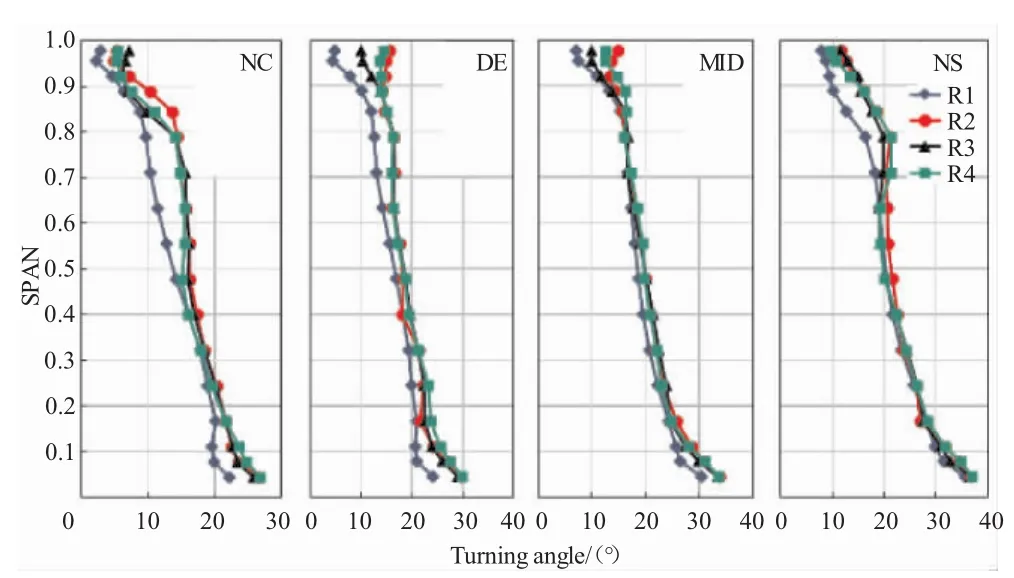
图12 不同流量状态下各级转子气流折转角展向分布对比

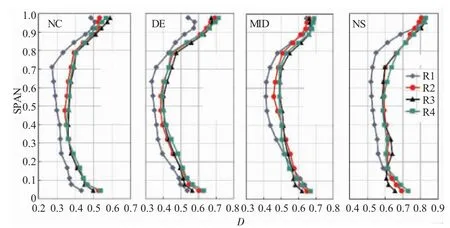
图13 不同流量状态下各级转子D因子展向分布对比

前3级静子在机匣轮毂处都没有间隙，第4级静子是悬臂安装，在轮毂一侧有1 mm的间隙。所以由流量展向分布来看，4个状态下第4级静子根部的流通能力较弱，这是由于泄漏造成的。不同流量状态下各级静子出口流量系数、D因子展向分布对比分别如图14、15所示。从图中可见，第2、3级静子出口截面流量的展向分布有很高的一致性，静子D因子沿展向的分布也是相同的规律，第2、3级静子基本一致。结合转子的流动特点，本文的4级重复级在第2、3级流场有很好的重复性。

图14 不同流量状态下各级静子出口流量系数展向分布对比

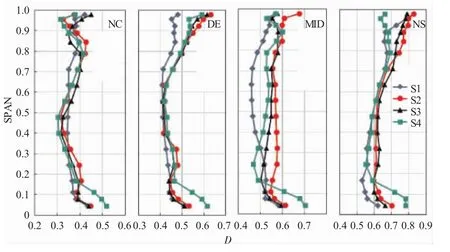
图15 不同流量状态下各级静子D因子展向分布对比

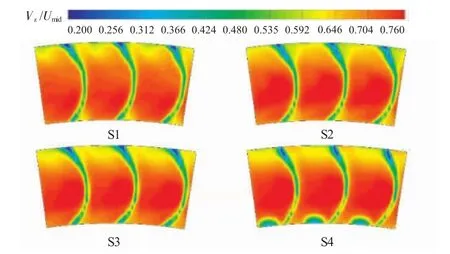
图16 近堵点各级静子出口无量纲轴向速度

3.3 静子出口流场

4种状态下各级静子出口的流场如图16～19所示。在每个流动状态都清晰可见，第4级静子叶根间隙泄漏所形成流动堵塞，在每个状态下静子出口流场结构清晰可辨且结构比较一致；随着流量系数的减小，静子的尾迹均匀增厚，但是并未发生明显的角区分离，可以看出本文4级重复级压气机静子的流场组织合理，是比较理想的压气机设计，也是高效率高压压气机的必要特征。

图17 设计点各级静子出口无量纲轴向速度

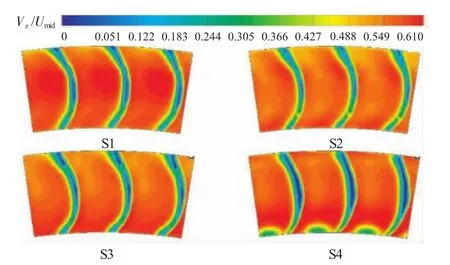
图18 中间状态点各级静子出口无量纲轴向速度

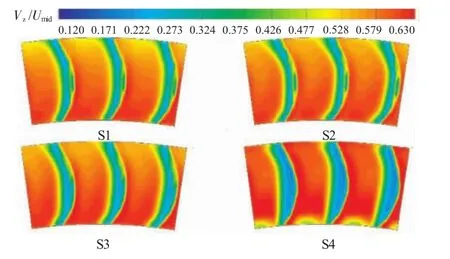
图19 近失速点各级静子出口无量纲轴向速度

3.4 低速模拟与高速原型对比

4级重复级第3级转静子进、出口的气流角与高速原型的对比如图20所示。从图中可见，转静子的进口气流角比较吻合，出口气流角有所偏差，但是分布规律较相似，这个偏差是由于低速情况下气流是不可压的，增加气流的折转来补偿高速气流的压缩性造成的。

图20 低速模拟试验进、出口气流角与高速原型对比

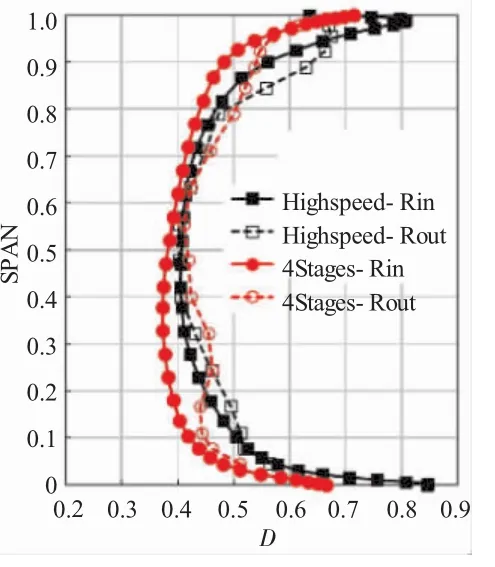
图21 低速模拟试验转、静子D因子与高速原型对比

4级重复级第3级转静子D因子与高速原型的对比如图21所示。从图中可见，转静子的D因子与原型的分布规律基本相似，低速模拟试验结果D因子稍偏大。总体来看重复级的设计较好地模拟出高压原型的气动参数的分布情况，其负荷水平和内部流动特点相对于当前的压气机设计水平来说具有典型性。

综上所述，4级重复级试验台是为了研究高压压气机后面级中的复杂流动，导叶的作用是为了给定下游转子的工作条件，前2级是最为重要的试验研究级，第4级是为了提供下游流场环境，减少设计和加工成本，通常选用重复级的形式。重复级最为核心的设计准则是在合适的雷诺数和马赫数条件下，保证进口来流条件相似的情况下，保证压气机级的进出口气流角和扩散因子等气动参数相似。在保证上述相关参数相似的情况下，其它气动参数基本相似。需要指出的是，这里无法保证速度三角形完全相同，只能保证级进出口气流角相同。为了保证负荷相似，叶片的弯角增大，因此转子/静子的出口/进口气流角必然不同，但这种不同是可以预知的，并且只有这样才能保证高速和低速情况的流动基本相似。

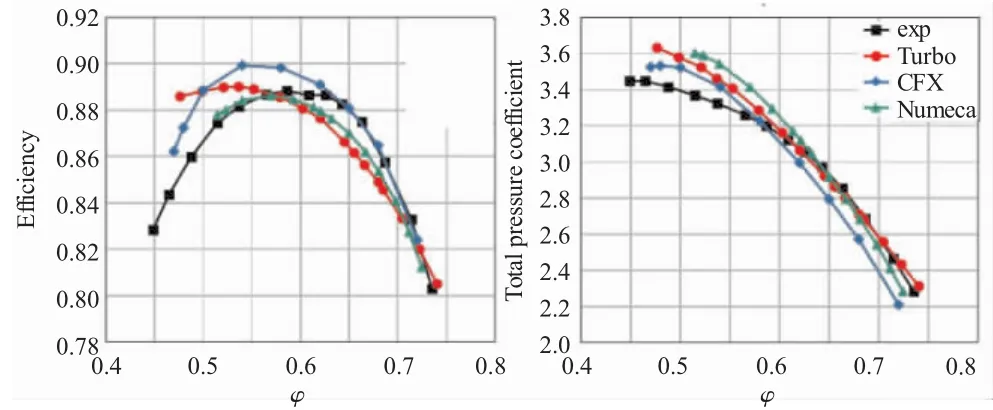
图22 4级重复级数值计算与试验的特性对比

4 数值软件的校验

4.1 特性

3维数值模拟结果与试验特性的对比如图22所示。从图中可见，对于效率特性，在大流量状态下，CFX、Numeca计算值比较吻合，Turbo计算值偏低；在小流量状态下只有Numeca计算值相差较小，CFX计算的效率整体趋势比较吻合，但是效率预估的太过理想，Turbo计算值也偏理想。对于总压升特性，在大流量状态下，Turbo和Numeca计算值比较吻合，但CFX计算值偏小；在小流量状态下，与试验值相比，3种软件计算值都偏高，Numeca计算值偏离得最远，CFX的最接近，Turbo的居中。3种计算软件在试验的近失速状态的算例均不能收敛，Numeca计算得到的稳定工作的流量范围最窄，Turbo的稍有增加，CFX计算的稳定工作的流量范围最宽但距离试验值还有一定差距。计算得到的重复级的综合裕度，Numeca的最低为21.47%，Turbo和CFX的相当，分别为 31.17%和32.94%，但是均比试验值39.04%的低。

由于是重复级设计，由前述试验数据分析，实际上各级的工作状态基本相似，在中间状态下Numeca和CFX计算的单级特性对比如图23所示。相对于Numeca而言，CFX计算的总特性效率偏高、总压升偏低的特点在每一级呈现相同的规律。下面进行第3级在设计状态和中间状态下气动参数展向分布和流场的3种软件计算值与试验结果的对比分析。

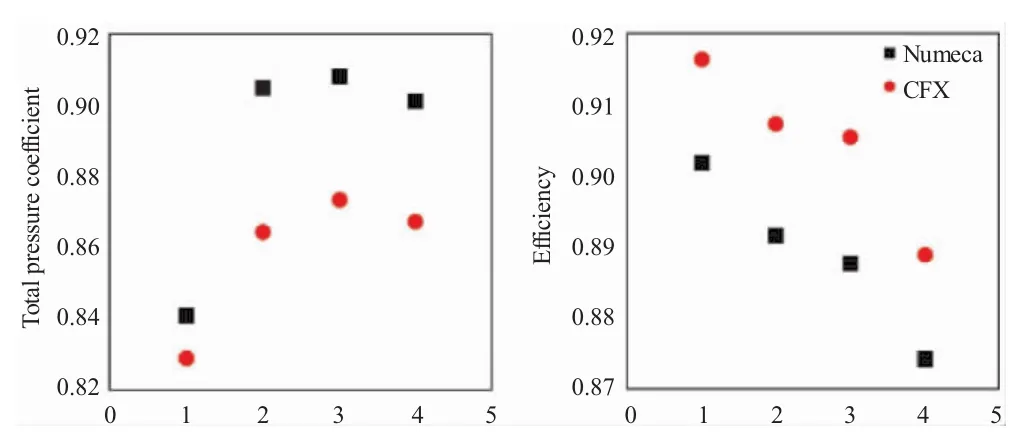
图23 中间状态下单级特性Numeca与CFX计算值对比

图24 设计状态下展向参数对比

4.2 设计状态

从图22中可知，在设计状态下的压气机总压升特性，Turbo计算值与试验值相近，CFX的偏小，Numeca的偏大。转子的总压升系数展向分布及静子的损失沿展向分布的对比如图24所示。从图中可见，对于转子总压升系数，Numeca计算值比试验值整体偏高，静子的损失水平相当；而Turbo转子总压升系数计算值在尖部比试验值低，但静子在尖部的总压损失也比试验值低，所以总压升特性与试验值相近；而CFX计算的转子总压升偏小，静子损失水平基本相当，故而计算得到的总压升特性比试验值偏低。

在亚声速转子中，转子的总压升与气流的折转角成正比，计算和试验得到的转子攻角、落后角沿展向分布的对比如图25所示，在设计状态下转子效率和转子气流折转角的展向分布对比如图26所示。从图中可见，转子攻角落后角计算值比试验值都有不同程度的偏差，Numeca计算值最接近，但是根部气流折转角比试验值大，CFX与Turbo计算值相当但均比试验值偏小。也就是说转子压升系数的差异本质上是由于数值模拟软件对于落后角计算的偏差使得叶片的工作状态与实际工作状态不一致造成的。

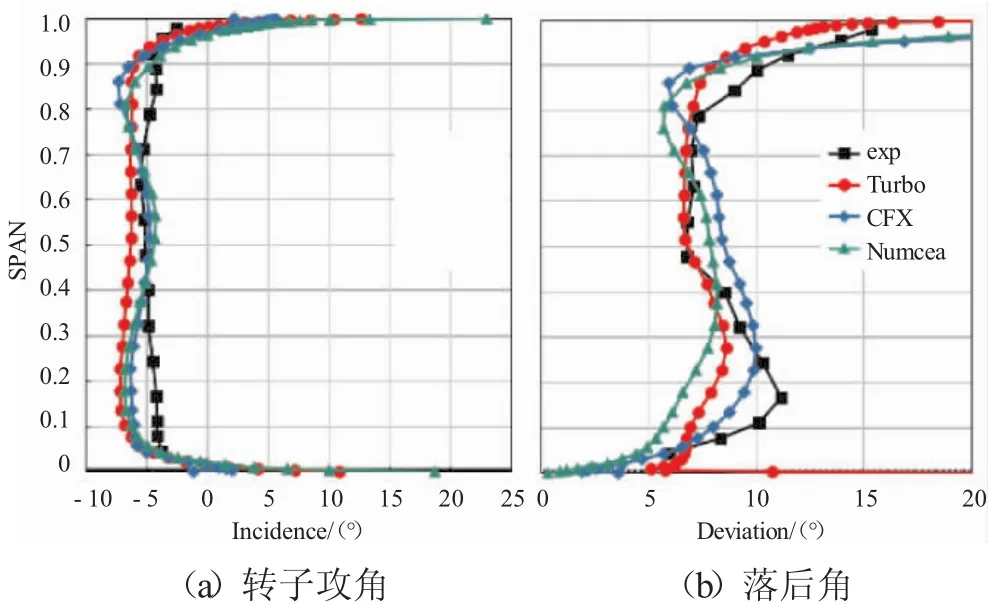
图25 设计状态下试验值和计算值对比

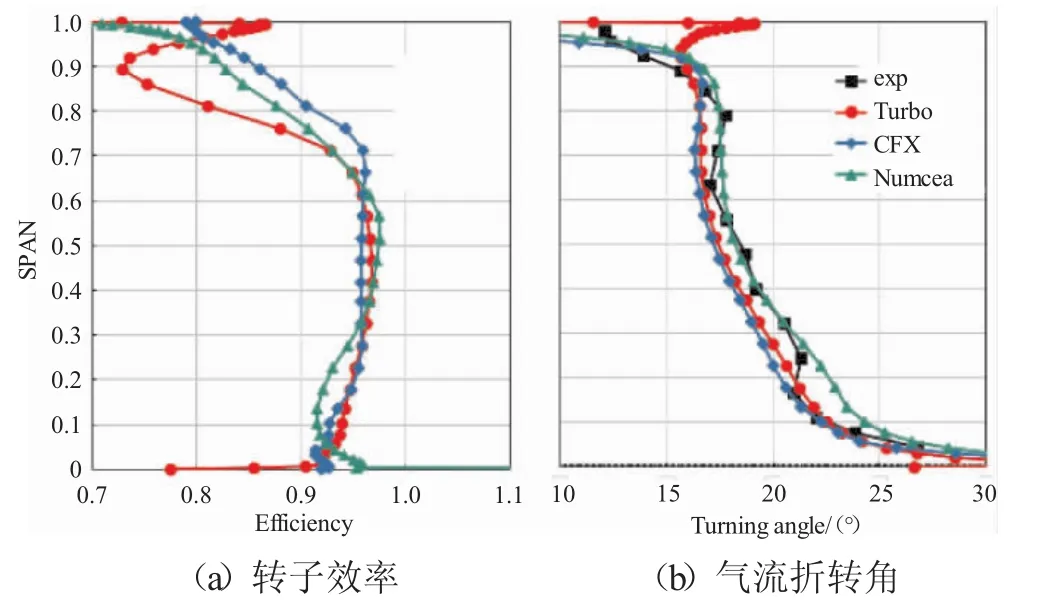
图26 设计状态下展向分布对比

对于在设计状态下压气机的效率特性，CFX计算值与试验值较接近，Numeca和Turbo计算值偏低，由于试验没有得到转子效率的展向分布，这里只给出3种软件得到的转子效率展向分布对比（图26左图），效率的差异主要集中在叶尖区域，Turbo计算的损失最大，Numeca的次之，CFX计算的尖区损失最小效率最高，正好与特性线上Turbo的最低，CFX的最高的计算结果对应。尖区效率不一致反映了各软件对于叶尖泄漏涡的模拟存在差异。

4.3 中间状态

在中间状态下转子总压升系数和静子损失展向参数对比如图27所示。从图中可见，对于在中间状态下的压气机总压升特性，3种软件计算值都偏高（图27左图），Numeca的最高，Turbo的次之。对于总压升系数，Numeca计算值明显偏高，CFX的稍高，Turbo的主流和根部稍高，70%～90%叶高偏低；但是对于静子的总压损失（图27右图），Turbo计算值明显偏低，所以总压升比试验值高，Numeca计算的根部损失偏大，尖部偏小，综合起来压气机总压升特性偏高，CFX计算值也呈相同的规律，只是偏高的程度没有Numeca的大。对比DE和MID2种状态下转子总压升系数展向分布的差别可见，随着流量的减小，CFD计算的总压升的增大程度要比试验值的增大程度大，也意味着转子的负荷随流量的减小增大得较快，这也是流量边界估计不准的原因。由于Numeca计算的负荷在相同的流量系数下最大，所以Numeca失速边界的流量最大，CFX与Turbo计算的失速边界相近，但也不能与试验值相吻合。

图27 中间状态下展向参数对比

对于在中间状态下压气机的效率，Numeca计算值与试验值比较接近，Turbo的偏高，CFX的最高。效率展向分布对比如图28所示。Turbo计算值仍然是尖区的效率最低，但是不同的是Numeca计算的根部的效率偏低，再加上Turbo对于静子的损失估计的理想，所以使得Numeca计算的效率比Turbo的低，CFX对于叶尖区域的计算过于理想，效率偏高，根部没有明显亏损，所以CFX计算的效率最高。

综上所述，数值计算主要在叶片的攻角落后角估计、叶尖泄漏的模拟及静子损失估计等方面存在不足，导致压气机特性模拟产生偏差，同时对于失速边界的估计也存在偏差。

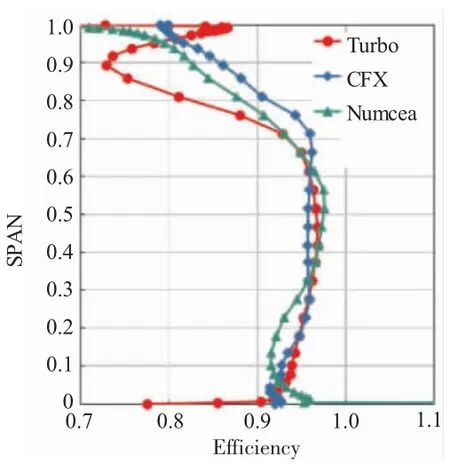
图28 中间状态下转子效率展向分布计算结果对比

5 结论

本文对某高压压气机后面级的4级重复级低速大尺寸轴流压气机进行了详细的试验测量和数值模拟对比分析，得到如下结论：

（1）获得4级重复级低速大尺寸压气机完整、详细的试验数据，利用小尺寸高精度5孔探针获得静子高分辨率的出口流场，可以清晰地分辨尾迹和角区等流动细节；

（2）流场测量结果表明，该4级低速模拟压气机实现了典型的重复级流动，较好地模拟了高压压气机后面级原型的流动特征，验证了原型压气机具有气动特征效率高和综合裕度大的性能优势；

（3）利用详细流场测量结果校验了常用3维计算软件Numeca、CFX和Turbo，校验结果表明：3种软件在估计叶片攻角、落后角、叶尖泄漏流等方面存在不足，无法准确估计压气机的特性，特别是近失速工况；

（4）4级重复级低速模拟压气机试验台为高压压气机后面级的关键技术验证和设计参数选择以及设计计算软件的校验提供了良好的试验手段及平台。