基于 IOWA 组合模型的高速铁路客运量预测研究

孙 丽，牟海波

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

0 引言

高速铁路具有快速、安全、舒适、低能耗等优点，被公认为是解决大城市间繁忙干线旅客运输的最佳交通运输方式。由于高速铁路建设投资大、造价成本高，预测运量不仅是决定高速铁路技术标准、设备数量、运营模式和行车组织的重要依据，更是决定项目经济效益、修建可行性的关键内容[1]。传统的组合预测方法是按照单项预测方法的不同而赋予不同的权重，同一种单项预测方法在样本区间上各个时点的权重是不变的，而在实际情况中，同一种单项预测方法在样本区间上不同时刻的预测精度是会发生变化的，即在某个时点上预测精度较高，在另一时点上预测精度较低。因此，一些学者提出了基于诱导有序加权平均 (Induced Ordered Weighted Averaging，IOWA) 算子的组合预测方法[2-4]，也有部分学者利用组合预测方法在运量预测方面进行研究。例如，武宁宁[5]采用 IOWA 组合预测模型预测分析了黑龙江省未来年份公路客运量的变化趋势；林德花等[6]将 IOWA 组合模型应用于短时交通流预测，建立了以整体预测误差平方和最小为目标的组合预测模型，并通过实例验证该模型的有效性；陈启明等[7]建立了基于 IOWA 算子 2 类准则下的最优组合预测模型，并将 2 类准则作为衡量模型优劣的标准，以广东省公路客运量为例进行分析说明；侯维磊等[8]基于 DRA-PCA-GA-BP网络模型对铁路货运量进行预测；张航等[9]建立了沪宁高速铁路旅客出行时间选择多项 Logit 模型，考虑旅客出行时间选择行为，并采用贝叶斯MCMC 算法求解。以上研究主要集中在公路交通量预测和铁路客货运量预测等方面。在此，研究通过采用 IOWA 算子，依据单项预测方法在样本区间上各个时点的预测精度从高到低按顺序赋权，以误差平方和为准则建立新的组合预测模型，并对我国高速铁路客运量进行预测，验证模型的有效性。

1 IOWA 组合预测模型

1.1 IOWA 算子概述

IOWA 是 2003 年由美国学者 Yager 提出的介于最大算子和最小算子之间的一种信息集成方法[10]。IOWA 算子可以表示为[11-12]

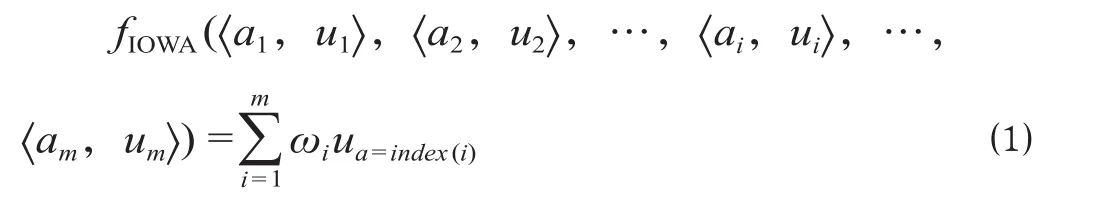
式中：fIOWA(〈a1，u1〉，〈a2，u2〉，…，〈ai，ui〉，…，〈am，um〉) 为 m 维诱导有序加权平均算子，简记为IOWA 算子，其中 〈a1，u1〉，〈a2，u2〉，…，〈ai，ui〉，…，〈am，um〉为 m 个二维数组，ui为第 i 种单项预测方法的预测值，ai为第 i 种单项预测方法的预测精度，又称为 ui的诱导值；ωi为第 i 种单项预测方法的加权向量，满足条件为预测精度序列 a1，a2，…，ai，…，am按从大到小的顺序排序后所对应的第 i 种单项预测方法的预测值。

公式 ⑴ 表明 IOWA 算子是对诱导值序列a1，a2，…，am按从大到小的顺序排序后所对应的u1，u2，…，um中的数进行有序加权平均，所对应的权值 ωi与数 ui的大小和位置无关，而与其诱导值所在位置有关。

1.2 IOWA 组合预测模型的构建

选择 f1，f2，…，fm共 m 种单项预测方法，通过对每个单项预测模型在相应预测时点按照预测精度从高到低赋予权系数，以误差平方和最小为准则建立 IOWA 组合预测模型。该组合预测模型的建模步骤如下[13-14]。

（1）计算单项预测方法在 t 时期的预测值和预测精度。选择单项预测方法 f1，f2，…，fi，…，fm，求出第 i 种单项预测方法在 t 时期的预测值 uit。在此基础上，计算第 i 种单项预测方法在 t 时期的预测精度 ait，可以表示为

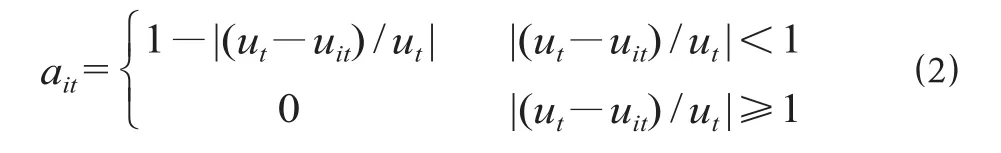
式中：ut为所要预测的实际问题在 t 时期的实际值。

把预测精度 ait看成预测值 uit的诱导值，这样 m 种单项预测模型在 t 时期的预测精度和其对应的在样本区间的预测值就构成了 m 个二维数组〈a1t，u1t〉，〈a2t，u2t〉，…，〈amt，umt〉。

（2）计算组合预测模型的预测值 fIOWA，即IOWA 算子值。对预测精度序列 a1t，a2t，…，amt按从大到小的顺序排序后，参考公式 ⑴，可得到 t 时期的 IOWA 算子组合预测值为

式中：ua-index(it)为预测精度序列a1t，a2t，…，amt按从大到小的顺序排序后所对应的第i种单项预测方法在t时期的预测值。

（3）计算 IOWA 组合预测模型的加权系数ωi。以 IOWA 组合预测模型的误差平方和最小为准则，构建最优组合预测模型，可以表示为

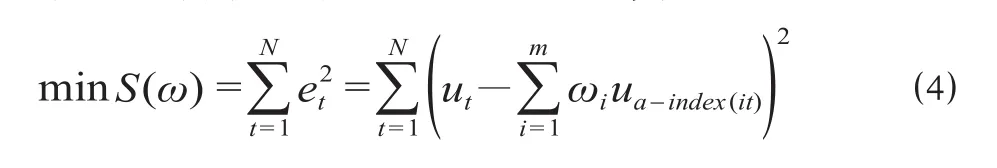
式中：S(ω) 为基于 IOWA 组合预测模型的误差平方和；et为 IOWA 组合预测模型在t时期的预测误差。

利用 MATLAB 最优化工具箱，可以得到基于IOWA 的组合预测模型的最优权系数ωi。

（4）基于 IOWA 组合预测模型计算t时期的预测值fIOWA。把计算出的加权系数ωi(i= 1，2，…，m)代入到公式 ⑶ 中，即可得到实际预测问题在t时期的组合预测值。

（5）判定 IOWA 组合预测模型的适用性。根据预测效果评价原则，记ut为原始数据序列，为预测结果，选取平方和误差、均方误差、平均绝对误差 3 个指标评价模型的适用性。其中，平方和误差平均绝对误差

分别采用 IOWA 组合预测模型和所选择的单项预测模型对实际问题进行预测，如果采用 IOWA 组合模型获得的上述 3 个误差评价指标值均比采用任何一种单项预测模型获得的上述 3 个误差评价指标值小，则可以选择采用 IOWA 组合模型对实际问题进行预测。

2 基于 IOWA 组合模型的高速铁路客运量预测

以我国高速铁路客运量为例，在考虑高速铁路客运量存在多重相关性影响因素和灰色特性的基础上，选择采用偏最小二乘回归 (PLS) 模型和灰色 GM (1，1) 预测模型，构建高速铁路客运量预测的 IOWA 组合模型，对我国高速铁路客运量进行预测分析。

（1）高速铁路客运量影响因素与基础数据的选取。高速铁路客运量影响因素主要包括：国内生产总值 (GDP)、居民消费水平、人口数、高速铁路营业里程、民航客运量、民用汽车拥有量及国内旅游人数。选取我国 2008—2016 年高速铁路客运量及其 7 个影响因素基础数据如表 1 所示。

（2）计算基于单项预测方法的预测值及预测精度。选择 PLS 模型和灰色 GM (1，1) 模型，对2009—2016 年我国高速铁路客运量进行预测，得到各单项预测模型预测结果如表 2 所示。

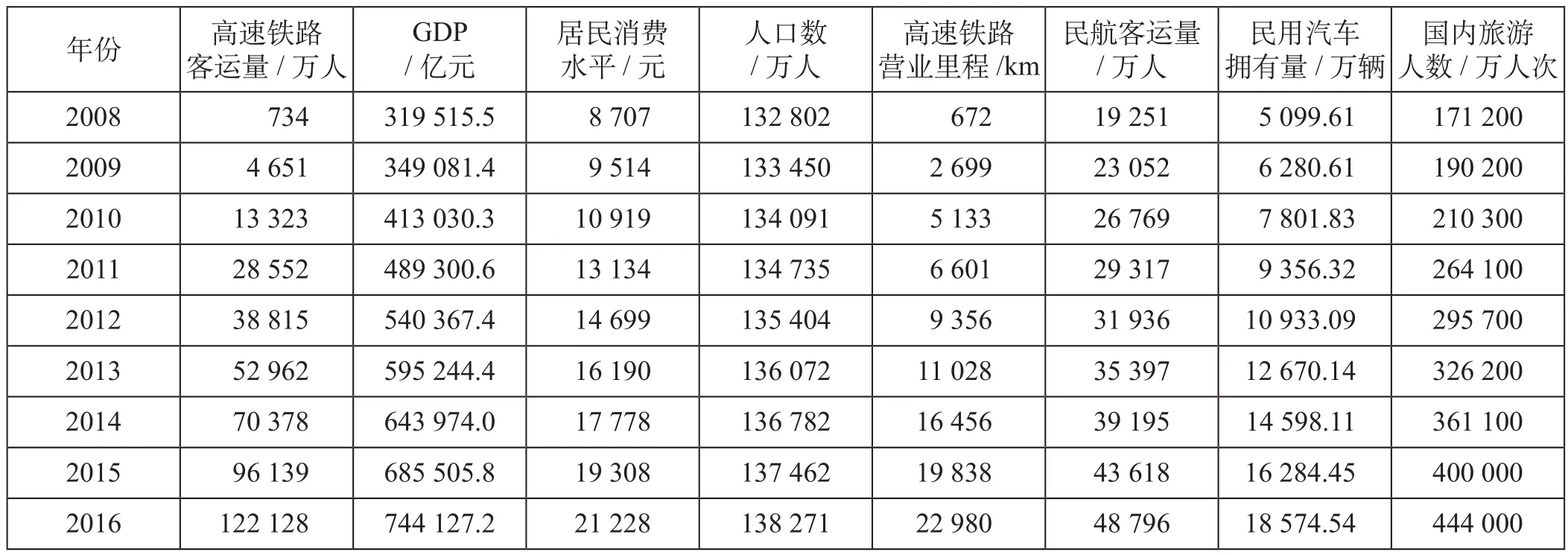
表 1 基础数据表Tab.1 Basic data

（3）计算组合预测模型的预测值fIOWA，即 IOWA算子值。根据表 2 可以构造出第t年预测精度和其对应的在样本区间的预测值的二维数组 〈a1t，u1t〉，〈a2t，u2t〉，根据公式 ⑶ 计算出相应的 IOWA 算子值。

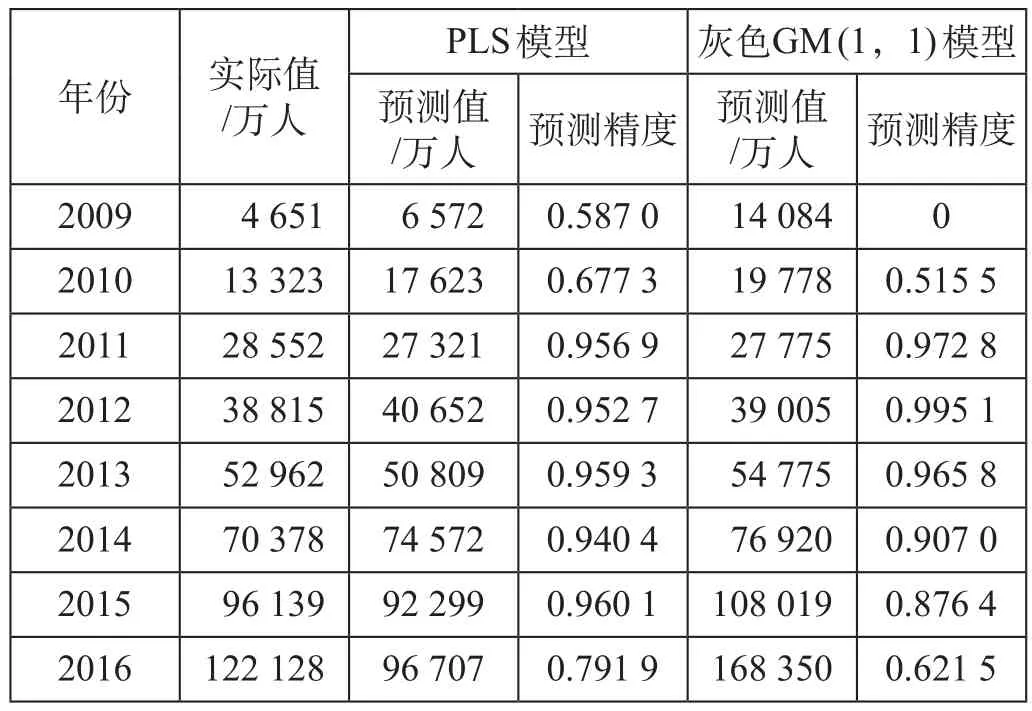
表 2 单项预测模型预测结果Tab.2 Prediction results of single forecast model

fIOWA(〈a11，u11〉，〈a21，u21〉) =fIOWA(〈0.587 0，6 572〉，〈0，14 084〉) = 6 572ω1+ 14 084ω2

同理，可以求得其他年份的 IOWA 算子值。

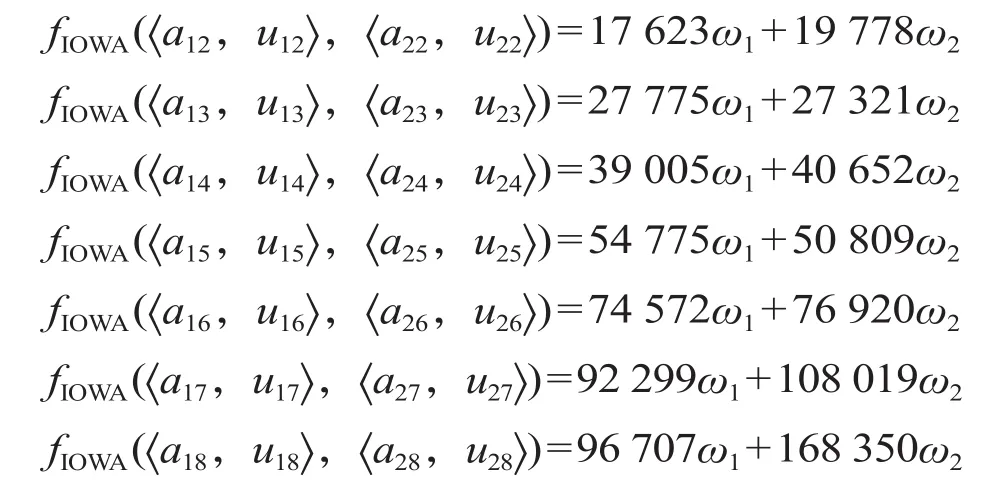
以上求出的 IOWA 算子值即为每年的高速铁路客运量组合预测值。

（4）计算 IOWA 组合预测模型的加权系数Wi。将预测误差代入到公式 ⑷ 中，可得到以下最优化模型为

minS(ω1，ω2) = (4 651－6 572ω1－14 084ω2)2+(13 323－17 623ω1－19 778ω2)2+ (28 552－27 775ω1－27 321ω2)2+ (38 815－39 005ω1－40 652ω2)2+(52 962－54 775ω1－50 809ω2)2+ (70 378－74 572ω1－76 920ω2)2+ (96 139－92 299ω1－108 019ω2)2+(122 128－96 707ω1－168 350ω2)2

利用 MATLAB 最优化工具箱，计算得到基于IOWA 的组合预测模型的最优权系数为ω1= 0.899 7，ω2= 0.100 3。

（5）基于 IOWA 组合预测模型计算t时期的预测值fIOWA。将计算得到的权值ωi代入到相应的 IOWA 算子值中，即可得到基于 IOWA 组合模型的高速铁路客运量预测值如表 3 所示。

（6）判定 IOWA 组合预测模型的适用性。将PLS 模型和灰色 GM (1，1) 模型计算得到的预测值与 IOWA 组合预测模型计算得到的预测值进行比较，预测结果分析如表 4 所示。

从表 4 可以看出，IOWA 组合预测模型的预测结果误差评价指标值均小于 2 种单项预测模型的预测结果误差评价指标值，表明 IOWA 组合预测模型在预测精度等方面具有明显的优势，适合用于我国高速铁路客运量预测工作中。

（7）“十三五”期间高速铁路客运量预测。根据《中长期铁路网规划》，到 2020 年铁路网规模将达到 15 万 km，其中高速铁路 3 万 km，覆盖 80%以上的大城市，同时根据我国经济社会发展现状，预测“十三五”末高速铁路营业里程为 3 万 km，假定从 2015 年以后至“十三五”末期间的营业里程按匀速增长来计算。对于其他影响因素的预测，可在历年的数据基础上，通过采用灰色 GM (1，1) 模型进行预测获得。2018—2020 年高速铁路影响因素基础数据预测如表 5 所示。

表 3 基于 IOWA 组合模型的高速铁路客运量预测值 万人Tab.3 Predictive value of combination forecast model based on IOWA

表 4 预测结果分析Tab.4 Analysis of forecast results

表 5 2018—2020 年高速铁路影响因素基础数据预测Tab.5 Basic data for passenger traffic volume forecast for 2018—2020

基于影响因素基础数据预测，通过 PLS 模型和GM (1，1) 模型对“十三五”期间我国的高速铁路客运量进行预测，利用最优组合权值 ω1= 0.899 7，ω2= 0.100 3，对这一时期的高速铁路客运量进行IOWA 组合预测，不同模型高速铁路客运量预测值如表 6 所示。

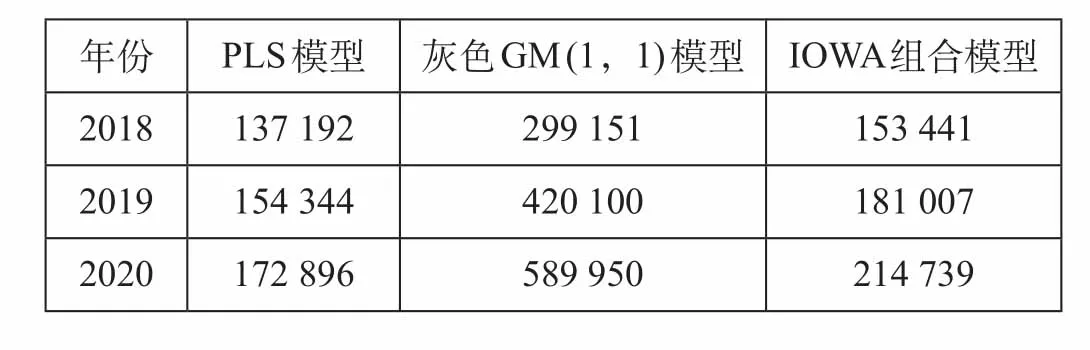
表 6 不同模型高速铁路客运量预测值 万人Tab.6 Predictive values using different models

由于 IOWA 组合预测模型是在各个单项预测模型的基础上所建立的，通过对预测效果评价指标验证，发现 IOWA 组合预测模型具有明显的优势，能够提高模型预测的精度。根据 IOWA 组合模型预测结果，2018 年我国高速铁路客运量将达到 153 441 万人，2019 年将达到 181 007 万人，而到“十三五”末期，在保持目前全经济社会增速和社会发展的趋势下，我国高速铁路客运量将达到214 739 万人。可以看出，未来几年我国的高速铁路客运需求会呈现不断上升的趋势，这主要是由于近年来高速铁路逐步成网，相比传统的交通方式，快捷、舒适、安全的高速铁路已经成为人们出行的主流趋势。

3 结束语

将 IOWA 算子系统地应用到高速铁路客运量预测中，以 PLS 模型和灰色 GM (1，1) 模型为单项预测模型，建立 IOWA 算子组合预测模型。运用该模型对我国高速铁路客运量进行定量预测，预测结果的误差评价指标分析表明，IOWA 组合预测模型的预测效果较好，能够有效提高高速铁路客运量预测的精度，对高速铁路客运量预测具有较好的适用性。由于影响高速铁路客运量的因素众多而且复杂，在影响因素选取时忽略了一些不能量化的突发事件等因素对其产生的影响，将在今后的研究中进一步完善。