ARIMA模型在甲型肝炎时间分布特征及趋势预测中的应用
朱佳佳,胡登利,吕 媛*
(1.湖南师范大学医学院,湖南 长沙 410013;2.中国人民解放军第163医院,湖南 长沙 410003)
甲型病毒性肝炎(Hepatitis A),简称甲肝,是甲肝病毒(Hepatitis A virus,HAV)引起的,主要经粪-口途径传播的急性传染病。甲肝在全球均有报道,但由于经济卫生条件差异,各个国家和地区 的甲肝流行趋势呈现明显差异。研究表明,收入水平和清洁饮用水可及性越高的国家和地区,甲肝发病率较低[1]。全球每年新发HAV感染者约140万人,我国各地每年均有病例报告,呈高度散发,暴发主要集中在学校等人群密集区域,西部地区省份发病率较高[2]。近年来我国甲肝发病率呈下降趋势,但发病人数中儿童和青少年占有很大比例[3]。本研究将采用自回归移动平均模型(autoregressive integrated moving average model,ARIMA)分析我国甲肝的时间分布特征并就发病趋势进行预测,探讨其在甲肝发病预测中的可行性。
1 资料与方法
1.1 一般资料
2004年1月~2017年12月全国各省甲肝月发病数监测数据,来源于“中国疾病预防控制信息系统”网络报告系统。
1.2 方法
基于2004年1月~2016年12月全国甲肝月发病数建立ARIMA乘积季节模型,并用2017年发病数据进行验证预测效果。统计分析采用SPSS 23.0。
ARIMA模型的建立过程主要分为以下几步[4]:原始序列平稳化处理、模型的识别、模型的参数估计和模型的诊断。
2 结 果
2.1 全国甲肝发病变化趋势
绘制2004年1月~2016年12月全国甲肝月发病数时间序列图(见图1),发现我国甲肝全年均有发病,但发病数逐年递减。每年6月~10月是发病高峰期,呈现一定的季节性波动,周期为12个月。故甲肝发病序列并不是稳定的时间序列。
2.2 时间序列的平稳化处理
对原始序列进行一阶普通差分和一阶周期为12的季节性差分后,发现时序图趋于平稳,且自相关系数函数图(ACF)截尾,偏自相关函数图(PACF)拖尾,说明此时的序列为平稳序列,符合ARIMA模型要求。
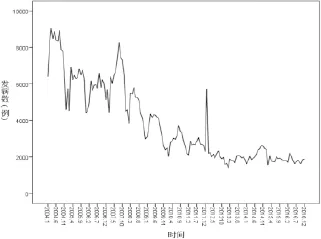
图1 2004年~2016年全国甲肝月发病数时间序列图
2.3 模型识别
由上述初步确定建立ARIMA(p,1,q)(P,1,Q)12模型,p,q和P,Q是连续模型和季节模型中的自回归阶数和移动平均阶数,需依据平稳序列的ACF和PACF确定。相关文献提示均不会超过2阶,故采用由低阶到高阶方式拟合模型。经比较,ARIMA(0,1,1)(0,1,1)12模型的标准化BIC最小(12.954),且R2(0.884)和标准化R2(0.381)较高,拟合优度较高,因此可视为本研究的最优模型。
2.4 模型参数的估计与模型诊断
ARIMA(0,1,1)(0,1,1)12模型残差的ACF和PACF均落在95%置信区间内(见图2),提示残差是随机分布的。模型的参数估计结果见表1,差异均有统计学意义(P<0.05)。Box-Ljung Q检验结果显示残差序列为白噪声序列(P=0.907),说明模型对数据信息的提取较为充分。

表1 甲肝发病数最优ARIMA模型的参数估计
2.5 模型预测
ARIMA(0,1,1)(0,1,1)12模型对我国2017年1月~12月的甲肝发病的预测值和实际发病数比较结果见表2。所有预测值均落入95%置信区间内,二者基本吻合,预测值与实际值之间的相对误差范围为2.4%~37.1%,说明该模型对我国甲肝的实际发病有较好的的预测能力。
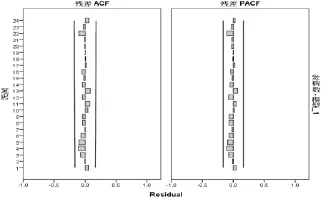
图2 ARIMA(0,1,1)(0,1,1)12模型残差序列的自相关系数图和偏自相关系数图

表2 2017年我国甲肝实际发病数与预测值比较
3 讨 论
时间序列分析[4]能将影响疾病发生的多种因素综合考虑于时间变量中,分析发病数据随时间发展变化规律,并能进行有效外推预测[5]。ARIMA模型是时间序列分析最常用的方法之一,本文将ARIMA乘积季节模型应用于我国甲肝的发病规律研究中,利用2004年~2016年共156个月份的甲肝发病监测资料建立的ARIMA(0,1,1)(0,1,1)12模型,较好地反映了我国甲肝发病序列的特征。2017年1月~6月的验证数据与实际值的吻合度较高,发病趋势与往年基本一致,相对误差较小,而7月~12月的预测数据相对误差较大,表明利用ARIMA乘积季节模型可以对我国甲肝发病趋势进行短期预测。
本研究的数据来源于我国传染病报告信息系统,质量可靠,但应注意的是,ARIMA模型适合疾病的短期预测[6],因此要不断纳入新的发病数据,调整模型参数以适应疾病的实际发生情况。此外,由于甲肝的发生还受诸多因素的影响,故后续研究中应尝试将影响因素纳入模型中以提高模型预测的精确性和准确性。

