高精度光斑中心定位算法

李道萍, 杨 波

(上海理工大学 光电信息与计算机工程学院, 上海 200093)

引 言

基于光学原理的三维测量,由于其具有高精度、非接触、易于控制等优点,日益受到人们的重视。光学三维测量的本质是通过分析被三维物体面形调制的光场分布来获得被测物体的三维信息。目标光斑对应的三维曲面上某点的高度是由该点在摄相机CCD表面的位置来确定的,那么光斑位置是否准确是决定测量精度的关键因素。目前比较常见的检测光斑中心的算法有灰度质心法、圆拟合法、Hough变换法以及多种改进算法等。

灰度质心法对于均匀光斑能够较准确定位,计算速度快,但是抗干扰能力差,对于情况复杂的实际图像,定位精度很差,而且只能定位中心,不能计算半径[1-3]。圆Hough检测是目前应用最为广泛的方法之一,其可靠性高,对噪声、变形、部分区域残缺、边缘不连续等有较好的适应性,但其缺点是计算量大,占据内存多,同时Hough变换需要对参数空间离散化,限制了检测精度,另外参数空间得票最多的点未必唯一,选择不同的点得到的图像空间曲线差异比较大[4-9]。圆拟合法时间复杂度较小,运算的精度很高,而且算法的速度非常快;但它也有十分明显的缺点,即抗干扰能力很差,当随机噪声存在时,中心运算精度会明显降低,当遇到很强的外界干扰时,所得到的圆心甚至可能会产生明显的错误[10-12]。

如果光斑光强分布均匀,使用恰当的算法可以使光斑定位精度达到亚像素级别,但是在一些实际测量中,光斑存在散斑,加之目标物体的反射以及各种干扰,使得CCD采集到的光斑强度极不均匀,严重影响了定位精度,上述方法均不再适用。为此,本文提出了一种光斑中心定位算法,该算法能够有效克服噪声及光强不均匀的情况,同时,通过选取合适的二值化阈值,不仅能够定位光斑中心,而且能够获取光斑半径。

1 传统中心定位算法

1.1 灰度质心法

灰度质心法就是应用像素的灰度值作为权重来计算光斑的质心,设图片的像素为m×n,每个像素点的灰度值为G(x,y),那么计算的质心(x0,y0)可表示为

(1)

1.2 最小二乘圆拟合法

基于圆拟合检测激光光斑中心的算法的依据是:采用最小二乘法的原理(残差平方和最小)来逼近激光光斑的轮廓。

最小二乘法圆拟合曲线为

R2=(x-A)2+(y-B)2

(2)

即

R2=x2-2Ax+A2+y2-2By+B2

(3)

式中:R为圆的半径;A、B为常数。

圆的另一种形式为

x2+y2+ax+by+c=0

(4)

令a=-2A,b=-2B,c=A2+B2-R2,则只需求出参数a,b,c即可求出圆的圆心和半径。

1.3 Hough变换法

Hough变换是利用点-线对偶性,将图像空间中的曲线通过曲线公式转换到对应的参数空间,对相同参数进行累加,那么图像空间的提取曲线就转化成求取参数空间的峰值问题。

f(a1,a2,…,an,x,y)=0

(5)

式中:(a1,a2,…,an)是参数空间中的点;(x,y)是解析曲线上的点,对于圆形曲线来说,半径是r,圆心是(a,b),解析式为

(x-a)2+(y-b)2=r2

(6)

那么,图像空间中的一个圆(xi,yi)对应参数空间中的一个点(a,b,r)。

圆变换的参数空间为三维的,在三维空间上进行数据累加的时间、空间消耗是非常大的。在具体应用中几乎是不可实现的。

2 光斑中心定位算法描述

图1为光斑中心定位的处理流程。

图1图片处理流程
Fig.1FlowchartofImageprocessing

准备一张如图2(a)所示的光斑图,首先将图像转变为灰度图像,使用最大类间方差法[13]找到图片的一个合适的阈值,然后在MATLAB中采用graythresh函数,最后用函数im2bw进行二值化,得到如图2(b)所示的二值化图像。选择合适的结构元素对二值图进行闭操作,闭操作通常能够消除狭窄的间断和细长的鸿沟,消除小的空洞,并填补轮廓线中的断裂[14],如I=imclose(IM,SE),(IM为待处理图像,SE为结构元素),进行闭操作后得到如图2(c)所示的图片。由于二值图的像素值只有0和1,首先运用find函数找到像素值为1的部分(即白色部分),并对其求均值得到(x0,y0),即

(7)

图2 图片处理流程Fig.2 Flow chart of image processing

这样就可以找到光斑圆心的大致位置。接着再找出图片中像素值为0的一系列点(x,y),然后进行以下循环:

(1) 求出距离圆心(xm,ym)(m=0,1,2,…)最近的点(xi,yi),距离为rm

(8)

(2) 移动圆心(xm,ym)使之与点(xi,yi)的距离在直线方向上增加1,即

(9)

此时,圆心位置进行了更新。

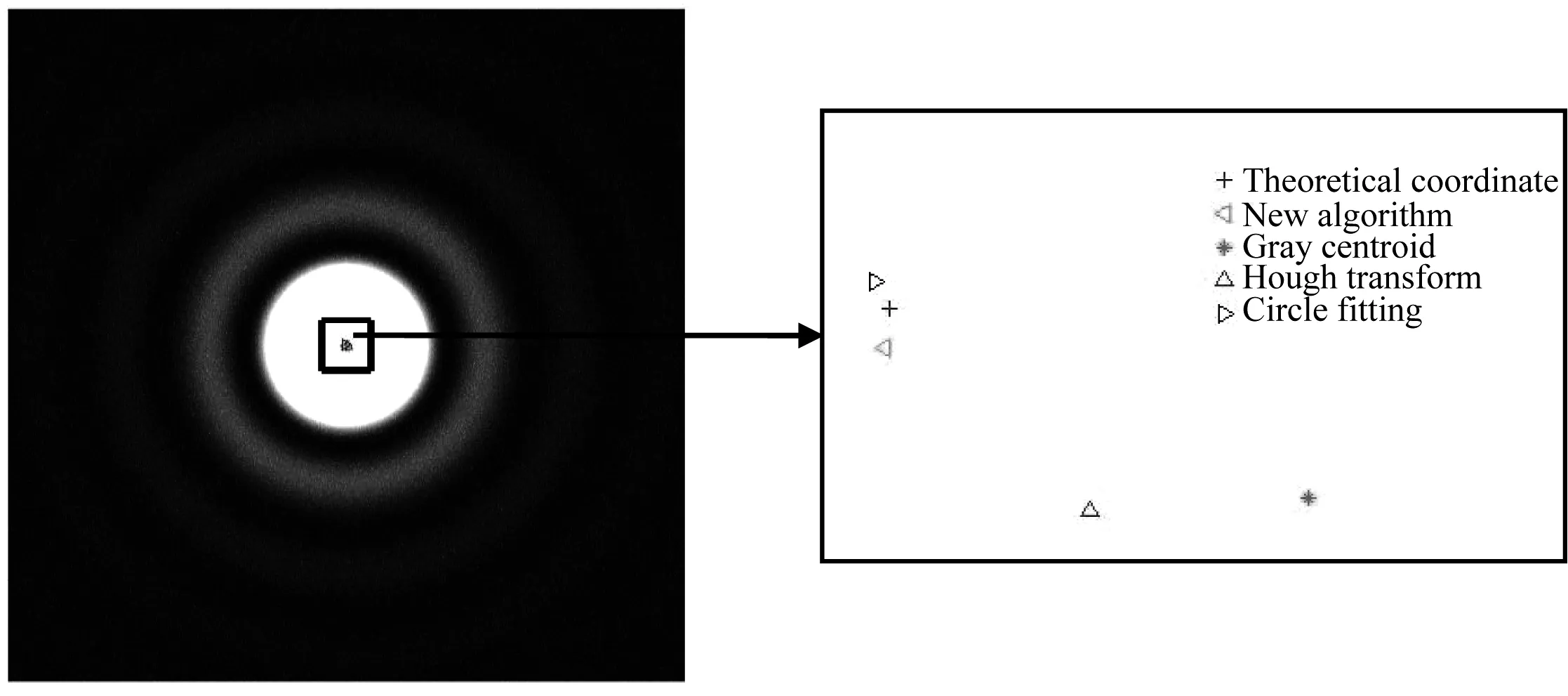
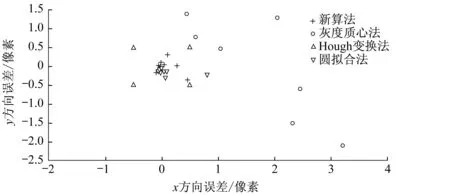
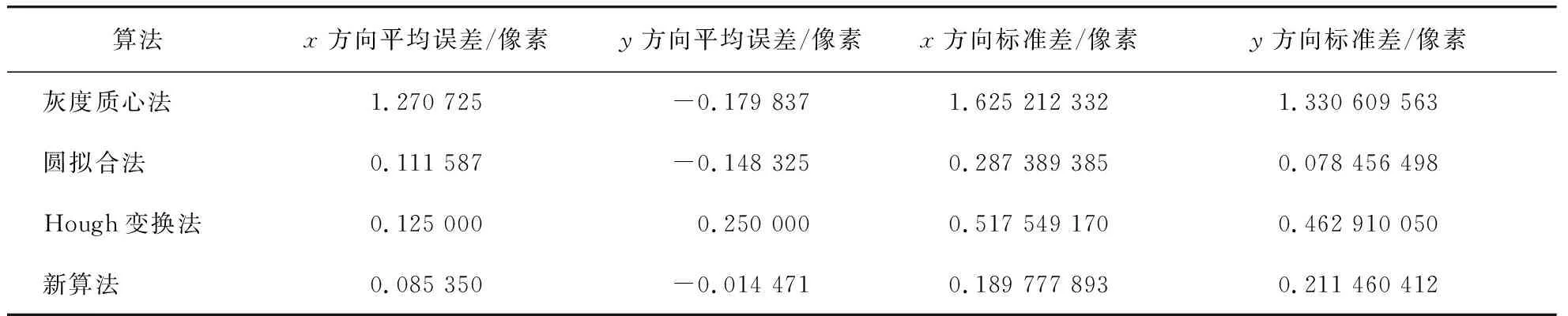
(3) 不断地重复(1)(2)步骤,每一循环需要判断计算出的距离是否小于上一循环的距离,直到计算出的距离rm+1

(4)求出距离点(xm+1,ym+1)最近的黑点,距离即为所求的半径rm+1,圆心为(xm+1,ym+1)。如图2(d)所示。

3 与传统算法的比较

用MATLAB产生一组夫琅禾费衍射光斑,图像大小为300×300,400×400,…,900×900,1 000×1 000共8幅图片,并对其加入随机噪声,如图3所示,采用4种中心定位算法计算其圆心位置。

图3 计算机生成的夫琅禾费衍射图样(含噪声)Fig.3 Computer generated Fraunhofer diffraction pattern(with noise)

应用新算法和其他3种算法分别对这8幅图像的光斑中心进行定位,得到中心坐标减去理论坐标后的误差,如图4所示,并对不同算法的误差进行了统计,如表1所示。从中可以看出,该算法误差小于0.5像素且比其他经典算法精度高,稳定性也最好。

图4 4种算法计算得到的8张衍射图样的圆心位置误差Fig.4 The error of the center location for 8 diffraction patterns calculated by 4 kinds of algorithms

算法x方向平均误差/像素y方向平均误差/像素x方向标准差/像素y方向标准差/像素灰度质心法1.270 725-0.179 8371.625 212 3321.330 609 563圆拟合法0.111 587-0.148 3250.287 389 3850.078 456 498Hough变换法0.125 0000.250 0000.517 549 1700.462 910 050新算法0.085 350-0.014 4710.189 777 8930.211 460 412

4 对实验生成的光斑进行定位

为了对算法进行验证,我们采集了两种光斑图样,如图5所示,(a)图为激光光源直接打在CCD上形成的图样,(b)图为夫琅禾费衍射系统接收到的图样。实验中采集到的光斑图像由于受到空气中杂质、CCD暗电流噪声、光子散粒噪声、反射面不均匀等的影响,不适用于直接提取光斑中心,在求取光斑中心之前,必须要对图像进行预处理以消除光斑外的小亮点、小暗点和其他杂散光的影响。从图中可以看出,新算法对光斑进行了较准确的定位,光斑轮廓拟合也很合理。

图5 光斑图Fig.5 Light spot

5 结 论

通过对常用定位算法的分析,提出了采用迭代法逐步逼近的方法计算出光斑半径及圆心。对计算机生成的8张含有噪声的衍射图样进行中心定位,并与其他传统算法进行比较,统计出各算法的误差,结果表明,该算法误差小于0.5像素且比其他经典算法精确。采用CCD相机、激光器等搭建了夫琅禾费圆孔衍射测试系统,经采集光斑图像并对其进行光斑定位,进一步验证了本文算法的正确性与合理性。