光的相干长度对两类光谱仪器分辨本领的影响

苑新喜

(中国地质大学(武汉) 数学与物理学院, 湖北 武汉 430074)

引 言

衍射光栅光谱仪和法布里-珀罗(F-P)干涉仪是两类常见的光谱仪器。借助于光的相干叠加效应,这两类光谱仪器比棱镜光谱仪有着更高的分辨率,因而在光谱线的精细结构研究中,衍射光栅光谱仪和F-P干涉仪这两类光谱仪器通常占据着非常重要的地位[1]。

光的相干长度是光波的一项重要特征参数。光的相干长度必定会对波列的叠加效果在某些方面产生一定的影响。但我们注意到,现有理论[1-7]在分析光栅光谱仪和F-P干涉仪的色分辨率时,完全忽略了光的相干长度对相干叠加效果的可能的影响。本文因此探讨了光的相干长度对这两类光谱仪器分辨本领的影响。

1 相干长度

在光谱仪的谱线图中,如果波长λ与其相邻波长λ+Δλ的同一级次的条纹(或主极大)恰好(或刚好)被区分开来,则该光谱仪的色分辨率RP=λ/Δλ。在讨论光谱仪的分辨率时,本文已假定光谱仪是无像差的理想光学系统[2]。

光的相干长度源自于对光源发光过程和干涉条件的认识。从波动的角度看,光源内每个原子的每一次发光只能发出一段长度有限的波列。在普通的光源内,各个原子的发光完全是自发的,各原子的各次发光是相互独立,互不相关。为了获得相干光,将普通的光源内同一原子的同一次发出的光分成两部分或更多,也就是把同一个原初波列分成两个或两个以上的子波列。从同一个原初波列分出的这些子波列如果能在空间某点相遇从而相互叠加,就会产生干涉现象。因此,这些子波列到达该点时的光程差必须小于波列的长度,否则彼此错开地通过该点而无法相遇和叠加。所以,波列的长度L就是产生干涉时光程差的极大值,这一极值长度称为相干长度,不少文献[8-9]对此都有着直观生动的示意图。光的相干长度表现了光的时间相干性,与光的相干长度等效的另外两个概念分别是相干时间[1,3-7]和光谱宽度[4-7],在此不再赘述。

普通光源的相干长度通常在毫米级到几十厘米之间[2-3, 6],跟激光光源相比这是很有限的。我们认为,只要涉及到光的相干叠加,特别是在使用普通光源的场合,就不能不考虑相干长度的有限性对干涉效果的影响。

2 光的相干长度对光栅分辨本领的影响

文献[1]给出了一维透射光栅色分辨本领的通用表达式:

(1)

式中:N为光栅的总的透光狭缝数;d为光栅常数;θ为衍射角;θ0为入射平行光与光栅平面法向的夹角;k为光的衍射(极大)级次。如图1所示,透光狭缝的长度方向垂直于纸面。Nd|sinθ-sinθ0|表示从光栅两端(相距Nd)衍射到θ方向的两条光线之间的光程差。从表面看,似乎N越大,光栅的色分辨本领越高。这个结论值得商榷,因为推导出RP=Nk的前提是从这N条透光狭缝衍射出的光线同时经过观察点而没出现相互错开现象,并没有考虑到光的相干长度的有限性。

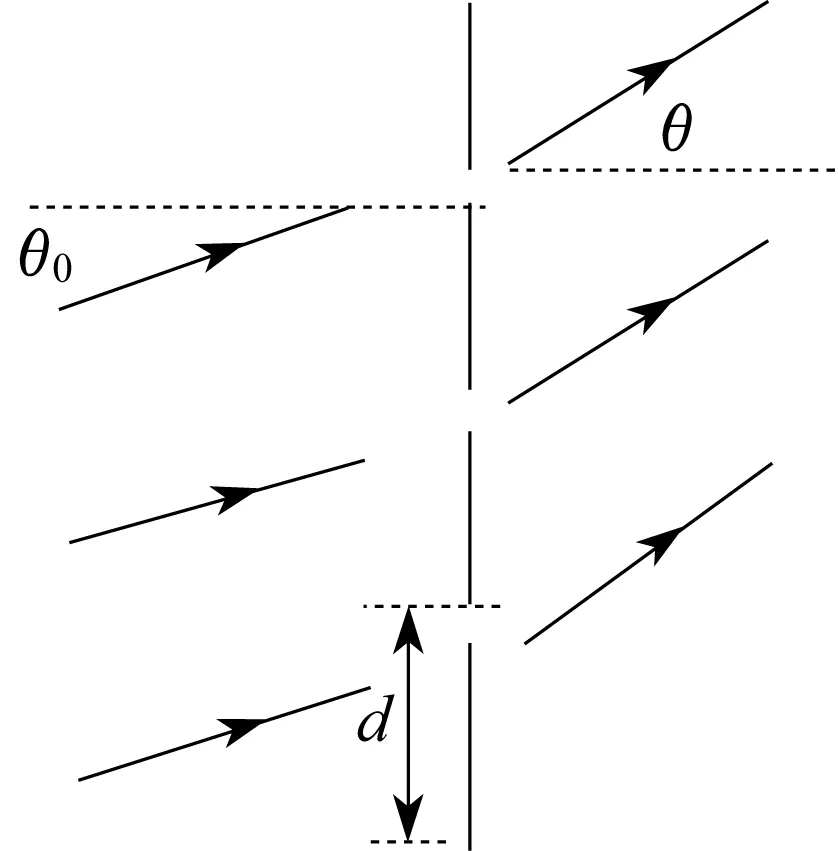
图1 一维透射光栅示意图Fig.1 Illustration of one-dimensional transmission grating

若考虑光的相干长度L,定义

N(L,θ)=[L/(d|sinθ-sinθ0|)]

(2)

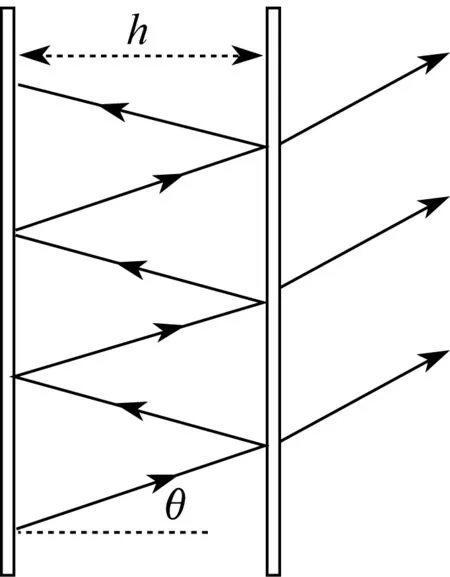
即N(L,θ)取小于或等于L/(d|sinθ-sinθ0|)的那个最大整数,N(L,θ)随着不同的光线的相干长度L与衍射方向θ的改变而改变。由于衍射光栅相邻透光狭缝的光程差d|sinθ-sinθ0|很小,N(L,θ)往往很大,常以百或千计。我们认为,当N>N(L,θ)时,光栅的分辨本领RP=N(L,θ)k

根据惠更斯-菲涅耳原理,光栅的每个透光狭缝都可以看成是发射子波的次波源,从每个透光狭缝出来的衍射光(子波列)因为光程不同,都会依次到达并通过观测点,不妨称该点为P点。相邻狭缝出来的衍射光(子波列)到达P点的间隔是d|sinθ-sinθ0|/c(c为光速)。第一个狭缝出来的衍射光(子波列)最先到达P点,但是波列长度有限(即光的相干长度L有限);当从第一个狭缝出来的衍射光(子波列)离开P点时,第N(L,θ)+1个狭缝出来的衍射光(子波列)才到达P点;当第二个狭缝出来的衍射光(波列)离开P点时,第N(L,θ)+2狭缝出来的衍射光(波列)才到达,依次类推。当倒数第N-N(L,θ)个子波列到达P点时,倒数第N-2N(L,θ)-1个子波列已离开P点,…,当最后一个狭缝出来的子波列到达P点时,倒数第N-N(L,θ)-1子波列已离开P点。同一时刻参与P点相干叠加的衍射光(子波列)的个数最多是N(L,θ)个,有N(L,θ)个衍射光(子波列)同时参与P点相干叠加的这种状态最长持续时间为(N-N(L,θ)+1)d|sinθ-sinθ0|/c。当N>N(L,θ)时,N再怎么增加,同时参与叠加的子波列数依然是N(L,θ),对应的分辨本领Rp=N(L,θ)k,也不会随着N的增加而提高,只会延长单个入射波列透射过光栅后在该处的所形成的最大光强的持续时间。

这里需要说明两点:一是光栅衍射可看成是等振幅、等相位差的相干叠加,这才使得上述公式Rp=N(L,θ)k直接套用了现有文献[1-7,9]推导出的公式Rp=Nk,推导过程因此从略;二是考虑了相干长度后,光栅色分辨本领Rp由Nk改写成N(L,θ)k,实际上是入射波列的单色性的一种体现。也就是说入射波列的自身单色性限制了光栅色分辨本领的充分发挥。这一点可理解为,如果入射波列的自身单色性很差,怎么能期望光栅将其与相近波长的其他波列分辨出来?

因此,定义N(L,θ)为给定相干长度L时在衍射角θ方向上的有效透光狭缝数。由于衍射角θ与衍射级次k有对应关系d|sinθ-sinθ0|=kλ,也可从另外一个角度将N(L,k)=L/(kλ)定义为第k级衍射的有效透光狭缝数。

总之,一般文献[1-7,9]所给出的衍射光栅的色分辨率Rp=Nk是有条件的,在光栅的透光狭缝总数小于或等于有效透光狭缝数(即N≤N(L,θ))时才能成立。

3 光的相干长度对F-P干涉仪分辨本领的影响

F-P干涉仪经常用来研究光谱线的精细结构。F-P干涉仪采用平行平面板产生多光束干涉条纹。构成干涉仪的两块平面玻璃板或石英板的内表面各镀有高反射率的部分透射膜,且相互平行,因而当中形成一个平行平面空气层。不妨设两内表面间距为h,光在两内表面之间来回反射时的反射角为θ,如图2所示。

图2 F-P干涉仪示意图Fig.2 Illustration of F-P interferometer

光的照射在正入射附近,因此θ趋于0。如果板面足够长,光在两个内表面之间反射的次数就会很大,透射出的光束数目N也就很大。不同于衍射光栅,这N条透射光束相干叠加不是等振幅、等位相差的相干叠加,而是振幅等比率衰减、等位相差的相干叠加[1-7],叠加后的合(复)振幅为[1,6]

(3)

式中:r′为光每次在内表面的振幅反射系数;t与t′分别是光在内表面的第一次入射时与最后出射时振幅透射系数;A(i)为入射光束的复振幅;δ为相继光束的位相差。易知,δ=4πn′hcosθ/λ,n′为平行平面之间空气(介质)层的折射率,λ为相应的波长。

常常为简化计算,取N→∞,r′2N=0。在这种情况下,这N条透射光束相干叠加后合振幅简化为[1,5-6]

(4)

完全与N无关。此时,相应的总透射光强[1-7]

(5)

该式就是平行平面板多光束干涉中的关于透射光的爱里公式,其中I(i)为入射光强,R=r′2为光每次在内表面的反射率,相关的透射率T=tt′=1-R[1]。

ε=2.07π/(S/0.97)=2π/S

(6)

I(t,N→∞)/I(i)随位相差δ变化的曲线如图3所示,在许多文献[1-7]中均有类似的图示。图3也给出了判据ε的示意图。

图3 I(t,N→∞)/I(i)随位相差δ变化的示意图Fig.3 I(t,N→∞)/I(i) as a function of phase difference δ

若R≈0.9,由mS所算出的F-P干涉仪色分辨本领高于一般的光栅光谱仪和棱镜光谱仪,但实际上F-P干涉仪不会达到这样高的分辨本领,文献[5]明确而简单地将之归因于谱线自身的宽度。从本文的观点看,实际上就是光的相干长度影响了F-P干涉仪色分辨本领的充分发挥。有限的光的相干长度意味着不是所有的透射光束能同时经过观测点而参与相干叠加,上面的推导中N→∞的取设应是有条件的。下面对此具体分析。

若考虑相干长度,同一时刻参与叠加的透射光光束数N(L,θ)依然是相干长度除以相继光束的光程差2n′hcosθ,即N(L,θ)=[L/(2n′hcosθ)],理由同前面衍射光栅的分析一样。同衍射光栅不同,F-P干涉仪中参数h较大(h甚至可高达10 mm[3],与一些普通光源的相干长度相当),导致相继光束的光程差较大。在这种情况下,可知N(L,θ)一般不是很大,有时甚至N(L,θ)<5,N(L,θ)的数值往往在十几到二十几之间。这时就不能轻易地取设N(L,θ)→∞,因此上述平行平面板多光束干涉中的关于透射光的爱里公式要相应地修改为

(7)

相比于原先的爱里公式,I(t,N=N(L,θ))比I(t,N→∞)多了一个因子式ξ=1+R2N(L,θ)-2RN(L,θ)cos(N(L,θ)δ),即I(t,N=N(Lθ))=ξI(t,N→∞)=ξζI(i)。易知,在反射率及相干长度给定的情况下,ξ也是位相差δ的单值函数,具有一定的周期性,但ξ的周期是ζ周期的1/N(L,θ)(注意,通常情况下F-P干涉级次m很高,级次变化不大时,如从m-1级变化到m级,对应光程差的变化相对很小,N(L,θ)可视为常数)。更为重要的是当ζ出现极大值时,ξ却出现极小值。不仅如此,若取R=0.87,N(L,θ)=16,则ξmin=0.796,ξmax≈1.23,(ξmax-ξmin)/ξmin>50%,(ξmax-ξmin)/(ξmax+ξmin)≈21%。这时,ξ因子对叠加后总透射光强分布的影响不可小觑,从而可明显影响干涉仪的分辨本领。I(t,N→∞)/I(i)(即ζ)与ξ均无量纲,且取值范围相近,为便于对比,本文将I(t,N→∞)/I(i)与ξ的随位相差δ变化的曲线画在一张示意图上,如图4所示,其中图中的ξ曲线取N(L,θ)=16。

图4 I(t,N→∞)/I(i)和ξ随位相差δ变化的示意图Fig.4 I(t,N→∞)/I(i) and ξ as a function of phase difference δ

如果仿照现有文献的方法[1,3-7],由上述I(t,N=N(L,θ))表达式去求解F-P干涉仪色分辨本领,由于I(t,N=N(L,θ))形式上远比I(t,N→∞)复杂,在数学上不太可能象I(t,N→∞)那样有单一而确定的代数表达式解。经过一些简单的数值估算后,对比ξ和ζ的二者关系,可得到如下几条定性结论:

(1) 反射率R越高,同时N(L,θ)越大,光的相干长度对F-P干涉仪色分辨本领影响越小。比如当R≥85%,N(L,θ)≥32时,其影响可以忽略不计,等同于现有文献中N→∞的结果,即Rp=mS。

(2) 反射率R不足够高,或N(L,θ)不足够大,相干长度对F-P干涉仪分辨本领将会有显著的影响。以位相差δ为自变量的I(t,N=N(L,θ))/I(i)函数曲线在峰值附近不再象I(t,N→∞)/I(i)那么尖锐,而会被ξ大大拉宽或拉平。同时,I(t,N=N(L,θ))/I(i)在其峰值附近剧烈变化,此时极有可能导致出现伪线。

(3) 反射率R不够高,同时N(L,θ)也不足够大,相干长度对F-P干涉仪分辨本领将会有很大的影响。

(4) 当N(L,θ)(ε/2)=π,即N(L,θ)=S时,以位相差δ为自变量的ξ函数曲线的极大值出现在ζ(即I(t,N→∞)/I(i))的半值附近,F-P干涉仪分辨效果大大降低,极有可能无法分辨。

(5) 当N(L,θ)(ε/2)=2π,即N(L,θ)=2S时,ξ函数曲线的极小值出现在ζ的半值附近,F-P干涉仪分辨效果大大提高,分辨效果最佳。

在实际工作中就要全面考虑具体的光源特性、F-P干涉仪的具体参数和实际看到的光谱线等情况进行综合分析和判断,以得到优良和可靠的测量数据。

由以上论述可以看出,N(L,θ)在分析F-P干涉仪的分辨本领时显得比较重要。将N(L,θ)定义为有效透射光光束数,此N(L,θ)与前面所述及的有效光束数S[1-2,5]有着本质的区别,前者由相干长度与对应的光程差决定,后者只由反射率R决定。

4 结 论

相干长度是光的一种本质属性。通过以上的分析可以看出,光的相干长度限制了同时参与相干叠加的光束数目,因此在一定条件下,光的相干长度对衍射光栅光谱仪和F-P干涉仪这两类光谱仪器的分辨率是有明显影响的,是不能完全忽视的。本文通过对衍射光栅光谱仪和F-P干涉仪这两类光谱仪器工作原理的进一步研究,弥补了现有理论中的一点不足,为这两类光谱仪器更好地在实际工作中应用提供了参考。