曲柄滑块机构等效转动惯量的计算及应用
牛瑞霞,张锦义,徐跃銮
(扬力集团股份有限公司,江苏 扬州 225127)
1 引言
曲柄滑块机构是压力机中最常见,也是应用最多的结构,考虑这种机构一般受非线性定常几何约束,因此该机构为完整的平稳系统,其自由度即为原动件数[1],当其驱动构件的运动已知时,其余构件的运动也就完全确定了。因此,可以采用等效力学模型来研究,这样系统动力学问题就转化成了一个等效构件的动力学问题,从而避免了联立求解各构件运动微分方程的麻烦,使问题得到了简化[2]。本文通过平面几何关系和刚体平面运动学规律,导出转化到原动件(曲柄)上的等效转动惯量计算公式,并且用一个曲柄滑块机构实例来说明等效转动惯量计算公式的应用,为该机构的运动过程动态仿真提供了理论基础[3]。
2 等效转动惯量的公式推导
将压力机中的曲柄滑块系统简化成平面连杆机构,单自由度的平面连杆机构中每个构件的动能分为两个部分:一是质心的平动动能,二是构件绕着质心的转动动能,即:

其中:m——构件的质量;
J——构件相对于质心的转动惯量;

图1 曲柄滑块机构简图
v——构件质心的速度;
ω——构件的角速度[4]。
图1中所示,杆2为曲柄,杆3为连杆,由运动分析,得:
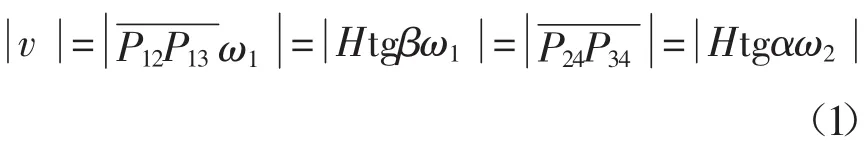
推出:
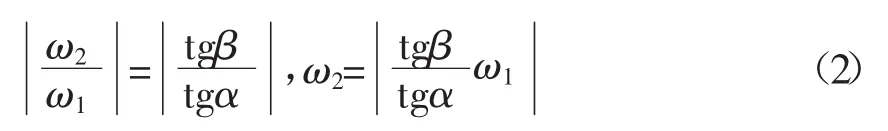
图中整个曲柄滑块机构的动能为:
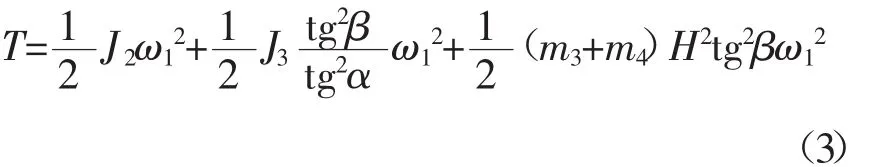
设整个系统相对于曲柄转动中心的转动惯量J,结合公式(3),得出:

根据图1并利用余弦定理求出下述公式:

因此有:

式中:J2、J3分别为曲轴和连杆的转动惯量,m3和m4分别为连杆和滑块的质量,可通过三维建模和运动的模拟得出,R为曲柄半径,L为连杆长度,代入公式,即可得出等效转动惯量和转角之间的关系,再结合图中三角函数的关系可得:

最终得出J于曲柄转角α的关系。
3 等效转动惯量的计算示例
下面以某种压力机的曲柄滑块机构为参考,建立数学模型,来说明等效转动惯量的计算和整个运动周期的变化情况。
如图1所示:假设该机构中曲柄长度R=70mm,连杆长度L=620mm,曲柄质量m2=98kg,连杆质量m3=125kg,滑块质量 m4=700kg,曲柄转动惯量J2=3301382kg·mm2,连杆转动惯量 J3=6604600kg·mm2,滑块的转动惯量Jc=0,设曲柄的转角30°,则通过计算得出,整个运动机构等效到P12点的转动惯量J为 5719531kg·mm2。
4 结论
(1)通过建立等效运动机构的方式,根据等效前后动能相等的关系,分析该机构的运动,得出单自由度曲柄滑块机构相对于曲轴支撑轴的等效转动惯量与曲柄转角、压力机工作行程等参数之间的关系及影响因素;
(2)结合三角函数,推导各个计算公式,最终得出等效转动惯量与曲柄转角的关系,同时可以看出等效转动惯量是周期变化的;
(3)通过解析计算公式,便于对平面曲柄滑块机构的动力学方程的仿真,为进一步分析曲柄滑块机构动态特性分析提供理论依据。

