基于SEM的BIM技术应用风险评价

李梦梦，赖芨宇，陈秋兰，易紫妮，孙晓丹

(1.福建农林大学 交通与土木工程学院， 福州 350002；2.福建省建融工程咨询有限公司， 福州 350001)

建筑信息模型(building information modeling，BIM)是在计算机辅助设计(CAD)等技术基础上发展起来的多维模型信息集成技术，是对建筑工程物理特征和功能特性信息的数字化承载和可视化表达[1]。运用BIM技术进行三维建模、碰撞检测等，可大量节省人力和物力，避免返工。在工程中合理使用BIM技术不仅能缩短工期，还能节省成本。近年来，BIM已成为行业关注的话题、政府关注的对象，并且引起了许多学者及专家们的极大兴趣。虽然BIM技术在建筑业领域有着极大的应用优势，但由于其风险因素的不确定性，仍然有许多企业持观望态度。新技术的使用使得建设过程中不确定性风险因素增加，可能导致项目决策失误，给企业带来致命的经济损失。对 BIM 技术应用过程中的风险因素进行识别，找出对项目影响最大的风险因素，并对应用BIM的风险进行评价，确定项目是否能应用BIM，能给项目决策者一个科学的决策方案，因此更多企业对BIM持乐观态度。

国内许多学者对BIM的应用风险进行了分析，但大多数为定性分析。本文对之前的一些研究成果进行总结，并咨询专家意见，对BIM技术应用风险进行了完善补充及合并，然后将这些风险因素划分成组织管理因素等4类。运用结构方程模型(structure equation model，SEM)进行数据分析，采用定性与定量分析相结合的办法，根据最后优化完成的模型路径系数的大小确定风险因素的大小，设置各风险因素的权重，对BIM的应用风险做出量化的表达公式，并用具体的案例来验证表达式的有效性，为项目决策者提供参考。

1 确立指标体系

1.1 指标建立

评价指标应具有代表性和针对性，既能反映正面影响，也能反映负面影响。指标选取应遵循科学性、客观性、全面性、可行性的原则，依靠科学、客观的理论来选取能全面反映BIM技术应用的风险。

通过大量的国内外文献研究，选取具有参考价值的文献20余篇，对其提到的BIM技术应用风险进行归纳总结，指标频数表格如表1所示。

由表1可知：大多数学者认为，BIM应用最大的风险就是缺乏标准规范，其次是协同的彻底性，而相关保险问题则是频数最少的一项。

1.2 指标确立

结合大量文献研究和专家咨询，初步选取具有代表性和针对性的指标，删除相关保险指标，添加BIM应用目标定位、投资回报期等指标，选择人员专业素质等15个因素作为2级评价指标，并将其划分为4个1级评价指标，设立评价内容。假设BIM应用风险分为100分，各2级指标满分为100分，采取加减分计分方式，其中对于2级指标采用考核方式，具体项目考核标准见表2。同时，为了便于建模，将各级指标用代号表示，如1级指标组织管理风险的英文表示是“organization management risk”，则选取“OMR”为组织管理风险代号，其他3个指标分别表示为“PR、ER、TR”。2级指标代号在相应的1级指标代号后加数字。

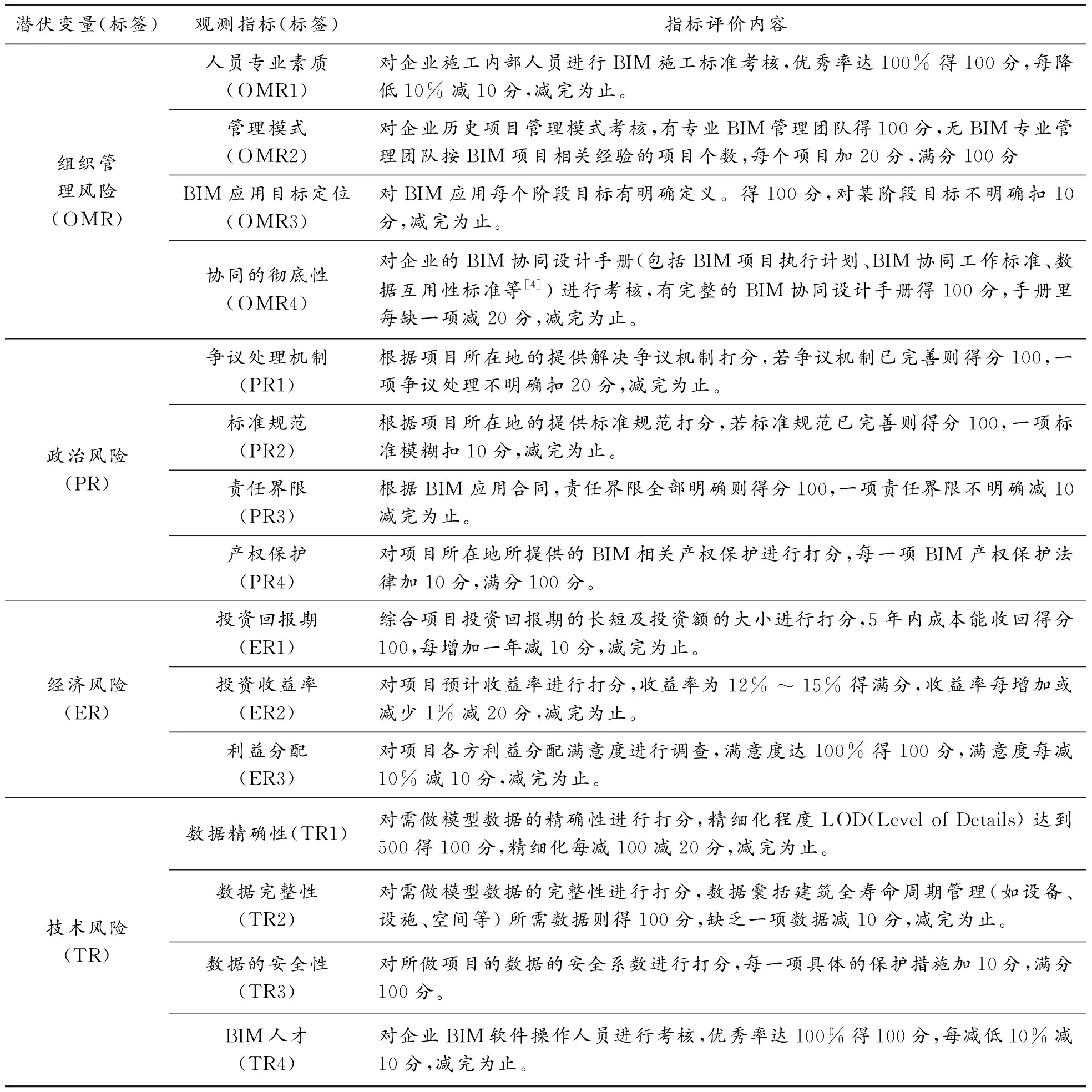
表2 观测指标

2 问卷数据整理

2.1 问卷设计与分析

问卷的发放形式为纸质问卷和网络问卷，其中纸质问卷均为现场填写及回收，网络问卷则设置一个IP只允许回答一次，避免受访者多次作答影响可靠性。问卷的受访单位包括BIM研发公司、咨询公司、施工企业、设计单位以及政府相关部门。本次调研中，纸质问卷共发放60份，回收52份，无无效问卷；网络问卷发放140份，回收124份，有效问卷112份，回收率为88%，回收有效率为93.1%。

2.2 调查数据的效度和信度检验

为了验证评价指标结构的效度，针对调查的数据，采用软件SPSS22.0中的因子分析对量表的效度和结构效度进行检验。KMO值和Bartlett球形检验结果见表3，总量表的方差统计见表4。

表3 KMO值和Bartlett球形检验结果

由表2可知：KMO值的检验结果为0.869，大于0.5，满足规定要求；P值为0.000，小于0.05，说明因素之间存在着一定的关联性，故而因子分析法的适应性得到了验证。

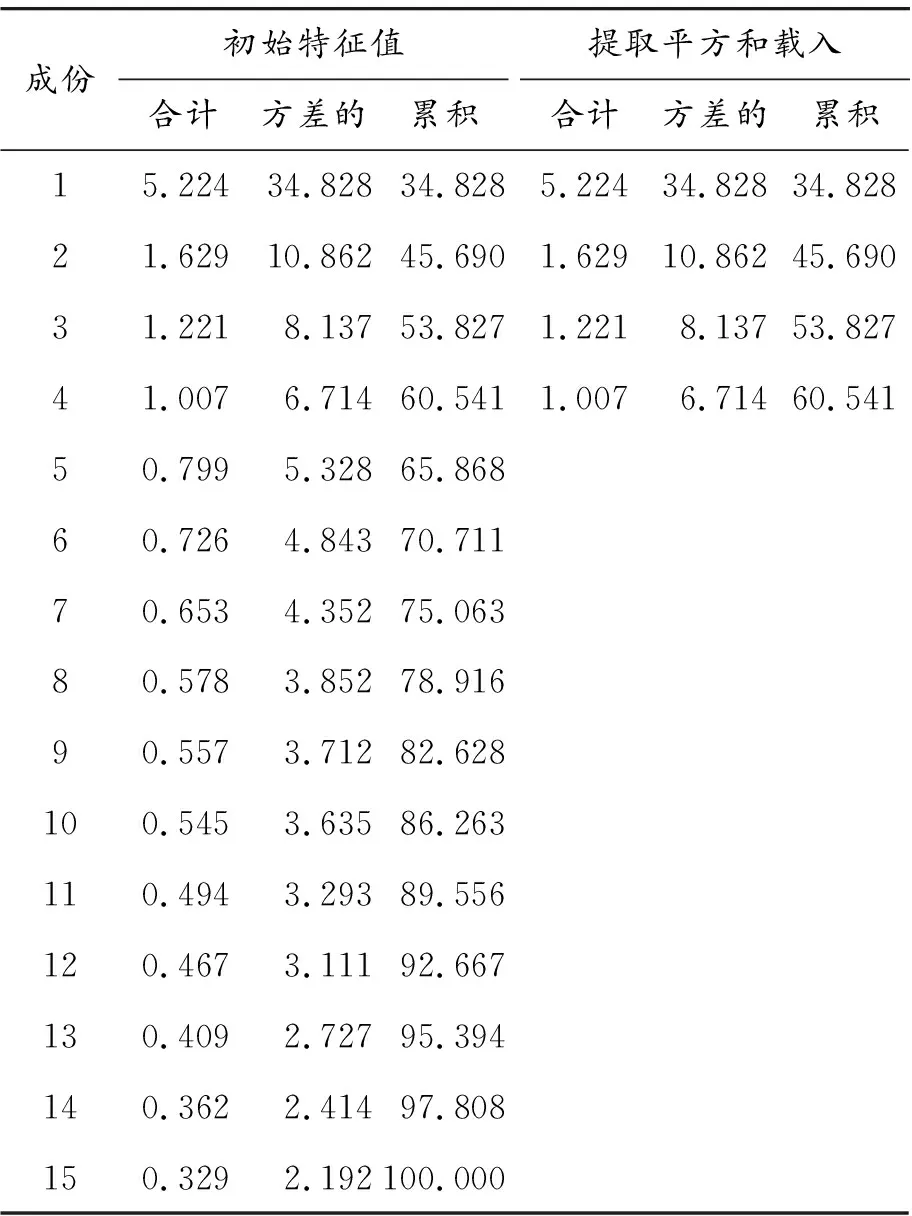
表4 总量表的方差统计 %

用主成分分析法对总量表进行因子分析，在结果中抽取4个主成分因子作为主因子，特征值大于1，积累的方差贡献率为60.541%，大于50%，表明该量表通过了结构效度检验，结构的有效性得到了验证。

为了验证评价指标的信度，采用SPSS进行可靠性分析，结果见表5。

由表5可知：Cronbach’s Alpha系数均大于0.6，而总的Cronbachs Alpha系数达到了0.869，说明问卷数据具有很高的信度。

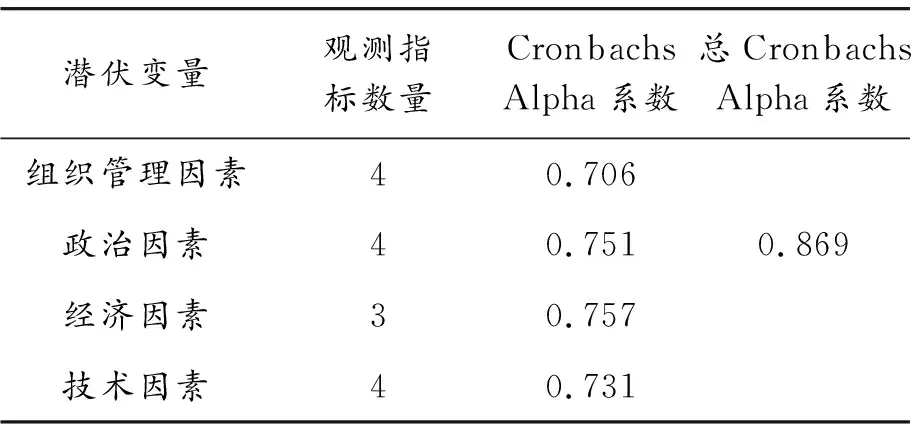
表5 信度检验结果

通过对问卷的效度和信度进行检验，最终结论证明了问卷的有效性和可靠性。对结构效度进行验证，证实问卷中的指标可以归为4类，因此结构效度得到了验证，可以进行下一步的模型构建。

3 SEM模型建立及分析

3.1 SEM模型建立

运用AMOS22.0软件对各个变量进行验证性分析，采用最大似然法对模型进行参数估计。采用路径系数作为参数以更加清晰地表示观测变量与潜在变量之间的关系[11]。基于模型拟合指数，在不影响原结构方程模型逻辑的情况下，对模型做适当的修正，改善模型配适度，以获得配适度较好的模型，最终的BIM应用风险的结构方程模型见图1。

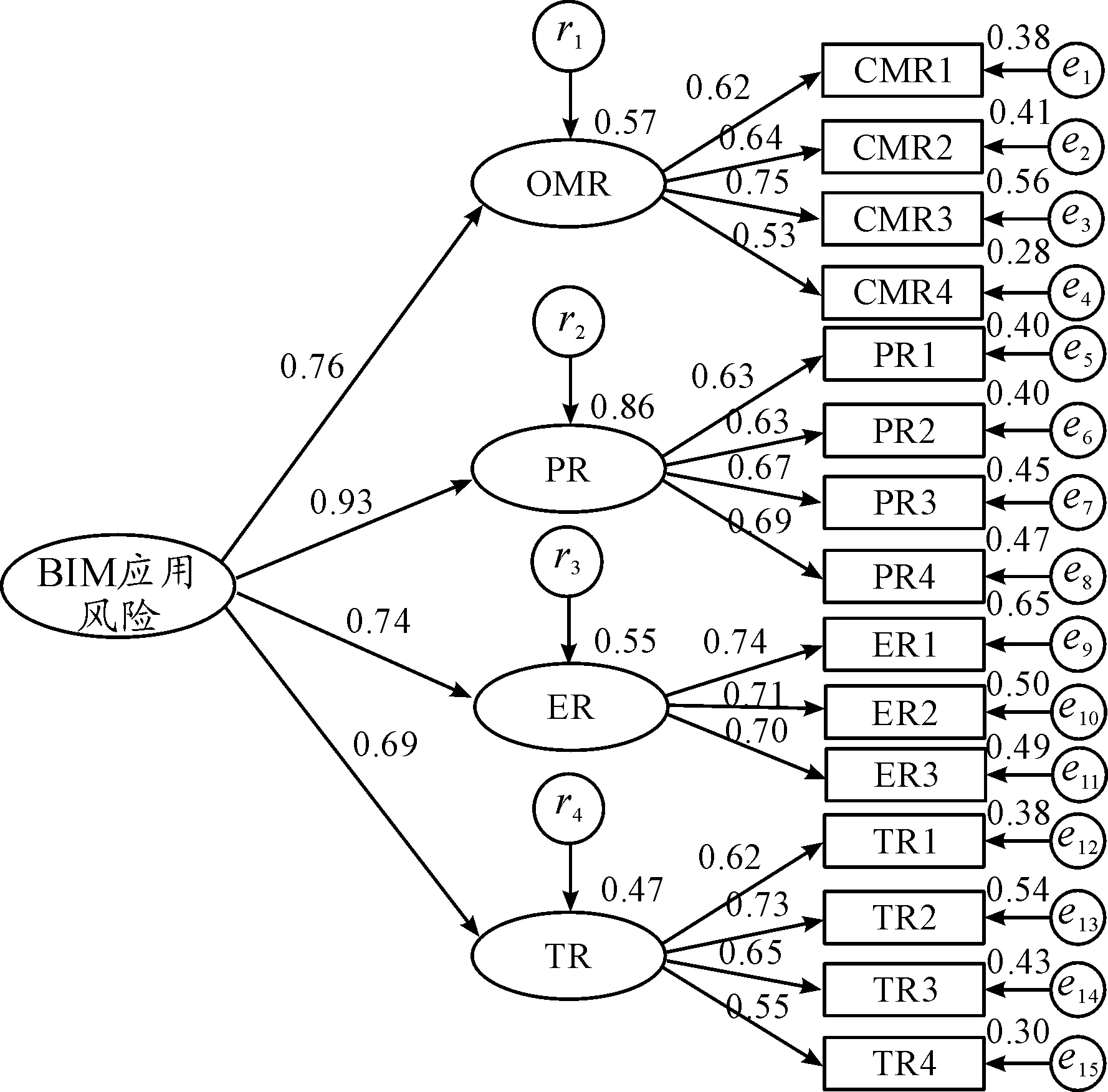
图1 BIM应用风险的结构方程模型

选取卡方与自由度之比CMIN /df、适配度指数GFI、非基准适配度指数NFI，比较适配指数CFI、近似均方根误差RMSEA、增量拟合指数IFI，对拟合指数TLI 等参数进行检验，从而考量模型的拟合优度[12]。经检验，修整之后的模型符合绝大多数指标的标准(表6)。

表6 整体适配度

3.2 模型分析与指标权重设计

结构方程模型的主要作用是表达潜变量之间的结构关系，从路径系数中体现这种关系。在风险评价结构方程模型中，路径系数代表指标间的关系，路径系数越大，说明指标对风险评价的影响程度越大[11]。结构方程模型路径系数的判别标准如表7所示。

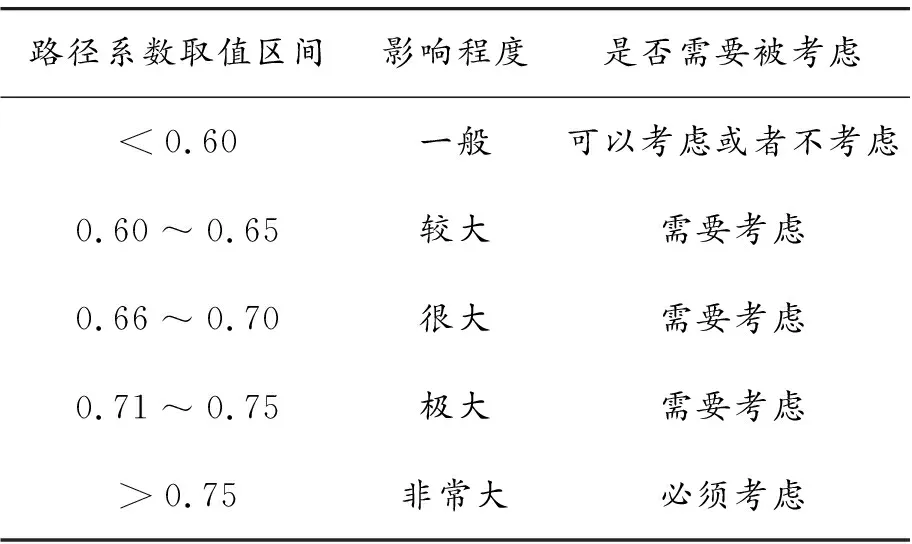
表7 路径系数判别标准

在图1中，e和r表示变量间的残差项，它们反映了结构方程中未能被解释的部分[12]。若残差项出现负值，则说明问卷本身有问题，需要重新设定及发放问卷。图1的残差项均为正值。对于结构模型的路径系数统计，4个1级指标潜变量的路径系数均大于0.6，说明它们对风险评价的影响很大，因此在信用评价过程中，这些都是需要考虑的变量。

设计指标权重值计算公式中，W(Fm)代表1级指标权重，W(Fmk)代表2级指标权重，依据路径系数，确立各指标的权重系数。各指标的权重系数如表8所示。

式(1)中：m为1级指标代号；k为级指标对应的2级指标代号；W为权重值；R为路径系数；F为1级指标；T为2级指标；Fm为第m个1级指标；R(Fm)为第m个1级指标路径系数；W(Fm)为第m个1级指标权重值。

m,k=1,2,3,4,5

(2)

式(2)中：Tmk为第m个1级指标对应的第k个2级指标；W(Tmk)为对应的权重值；R(Tmk)为对应的路径系数。

Wmk=W(Fm)×W(Tmk)

(3)

式(3)中Wmk为各2级指标最终权重值。

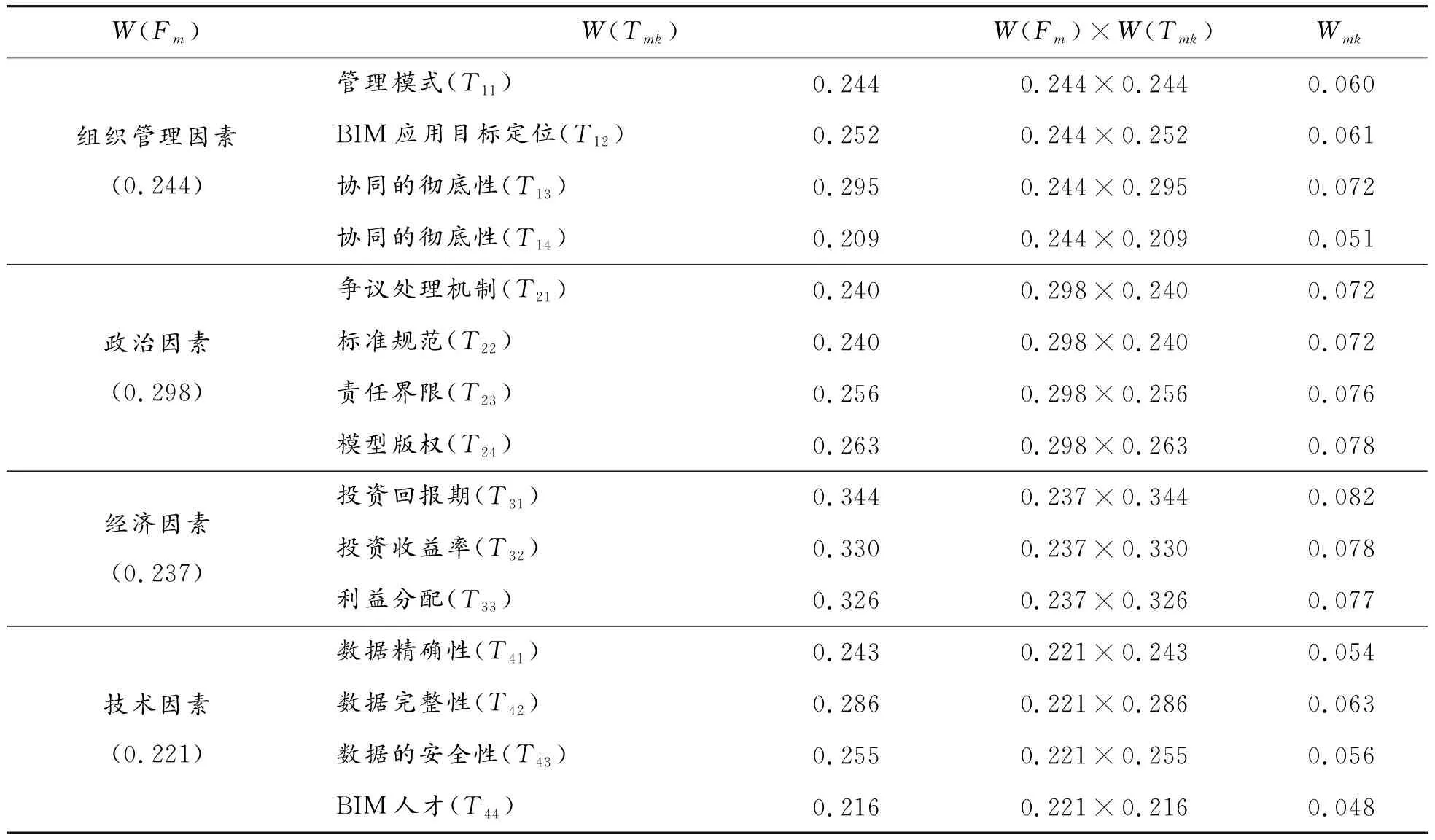
表8 各级指标权重系数

3.3 评价方式设定

采取计分制度，对2级指标的具体评价内容进行评分，把最终得到的每个2级指标的分数值记为Xij(i=1，2，3，4；j=1，2，3，4)，表示为第i个1级指标中的第j个2级指标；1级指标对应的数值记为Yk(i=1，2，3，4)，将风险的总得分记为S，得出：

S=Y1+Y2+Y3+Y4

(4)

Y1=0.060X11+0.061X12+

0.072X13+0.051X14

(5)

Y2=0.072X21+0.072X22+

0.076X23+0.078X24

(6)

Y3=0.082X31+0.078X32+0.077X33

(7)

Y4=0.054X41+0.063X42+

0.056X43+0.048X44

(8)

依据风险评价计算公式，对风险大小进行评级划分，设定风险等级划分区间，如表9所示。

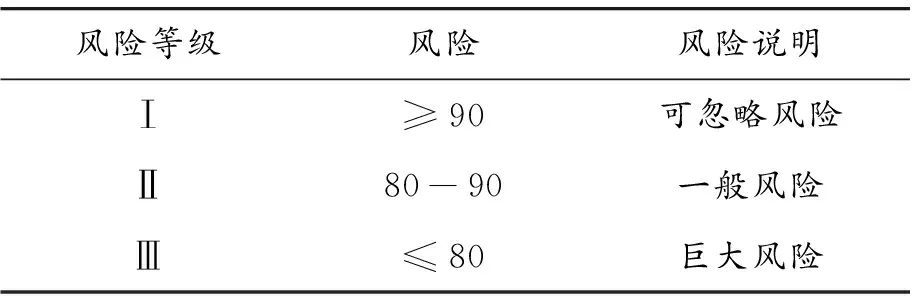
表9 BIM应用风险等级评级标准

4 案例实证分析

为了验证公式的有效性，对某总承包公司在福建省泉州市某项目BIM应用风险进行评价，得分情况见表10。

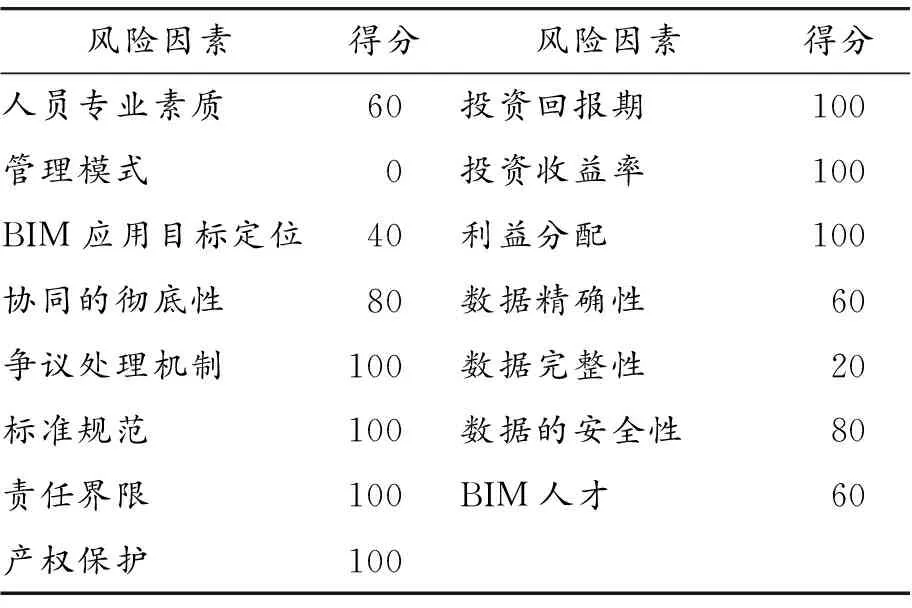
表10 风险评分结果

根据表10中的风险因素得分，应用式(5)～(8)，计算得到1级指标Y1=15.38，Y2=29.8，Y3=23.7，Y4=11.86，再代入式(4)得到应用风险的总得分S=80.74。根据表9可知：该公司在泉州某项目的BIM应用风险等级为Ⅱ级，因此该企业决策者应慎重考虑项目是否使用BIM，或者选择合理的组织管理模式来减少风险。

5 结束语

本文以BIM技术为研究对象，分析了其在应用时存在的风险，运用定性和定量相结合的方式对BIM技术的应用风险进行建模分析，设定了风险评级，为BIM技术的应用风险提供了具体的公式作为评价依据，给项目决策者提供了可以量化风险的考核方式做参考，有助于更直观地决策项目是否使用BIM技术，进而选择合适的应对方案，避免因决策失误给企业带来的损失，让BIM技术的应用更合理，最终促进BIM技术在建筑企业领域的蓬勃发展。