基于Matlab/Simulink的发动机扭振实时模型的建立
石晓辉,汪杨凡,李文礼,,王晶晶,张向奎,何 洋
(1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;2.重庆工程职业技术学院, 重庆 402260;3.重庆青山工业责任有限公司, 重庆 402761)
发动机高瞬态扭振模拟技术是汽车传动系动态模拟试验的关键技术之一[1-3]。发动机具有无限多阶的振动模态,轴系会按其受到的激振载荷的频率进行强迫振动。发动机扭振模拟技术可以再现实车扭振激励信号,该信号可以作为传动系NVH台架与变速器硬件在环试验等试验的激励源,能比较真实地复现实车运行状态,便于研究被测部件运行特性受到扭振激励的影响。若要在室内台架上模拟发动机扭振激励对传动系统被测件的影响,则需要一个高动态响应的发动机实时控制模型作为激励源。因此,如何建立一个高动态响应的发动机高瞬态扭振实时控制模型是发动机高瞬态扭振模拟技术的关键与难点[4-6]。发动机扭振模拟技术是一个集机械、电子、控制等多学科为一体的复杂学科,国内外众多学者对其进行了研究,为发动机扭振模拟技术的发展作出了贡献[7-8]。
发动机扭振模拟技术在很多文献中都有论述。文献[9-10]分别提及到了黑箱模型和基于物理结构的模型。然而这些模型对发动机的开发参数依赖过大,且在模拟过程中很难满足高动态控制响应的要求,因此不适用于台架模拟试验。文献[5]采用了高频液压控制器与自使用闭环控制,可以得到比较真实的扭振曲线,但是该种方案下液压控制系统维护比较困难。文献[6]建立了基于交流异步电机模拟汽车发动机的非线性系统模型,并分析对比了开环转矩补偿法和带有开环转矩前馈的闭环转速控制法之间的优劣。
笔者以某款发动机为参考,利用Matlab/Simulink建立了一套可以应用于汽车试验台架的发动机高瞬态扭振实时控制模型。
1 发动机高瞬态扭振实时控制模型
激振载荷是引起系统轴系振动的能量来源,对于发动机轴系来说主要的激励载荷分为3种,即发动机运动部件的惯性载荷引起的激振力矩、发动机工作时由于汽缸内气体比力变化而引起的激振力矩、接受功率的部件吸收功率不均匀而产生的激振力矩。其中前两种激振力矩为引起发动机轴系扭振的主要因素,第3种激振力矩对车用发动机的影响很小,这里不对其进行讨论。因此,总的发动机扭矩可以表示为:
Ten=TI+TC
(1)
式中: Ten为总的发动机扭矩(N·m); TI为往复惯量引起的激励扭矩(N·m); TC为燃烧压力引起的激励扭矩(N·m)。
2 发动机惯量扭矩模型
发动机曲柄连杆机构的惯性力分为离心惯性力和往复惯性力。离心惯性力作用方向始终通过曲轴回转中心,故它对曲柄的作用力为0,不会引起扭转振动。而其往复惯性力通过连杆作用在曲柄销上产生周期性变化的切向力矩,该力矩即为引起轴系扭振的动力。单缸往复运动惯性力模型如图1所示。

图1 单缸往复运动惯性力产生的激振力
往复惯性力为:
pj=-mja=-mjrω2(cosα+λcos2α)
(2)
上述往复惯性力通过连杆轴颈对曲轴形成的力矩为:
将式(1)代入式(2)可得:
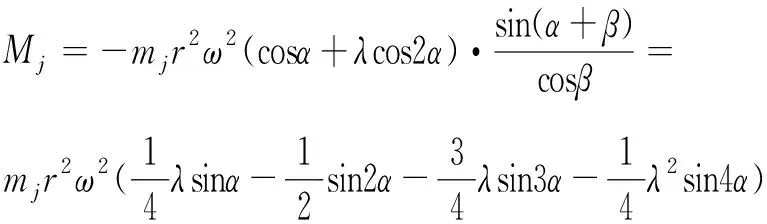
(4)
式中:mj为单个汽缸往复运动质量(g·s/cm); r为曲柄回转半径(cm); α为曲轴转角(rad); λ为曲柄连杆机构常数,λ=r/L;L为连杆长度(cm)。
激振力矩Mj虽然可以分解成很多的简谐力矩,但是在计算到第4阶时已经可以满足实际应用中的精度要求。
3 发动机燃烧扭矩模型
3.1 基本微分方程
联立能量守恒方程、质量守恒方程、理想气体方程3个方程构成描述发动机缸内实际过程的基本微分方程组[2-3]:
使用欧拉法对方程组(5)进行数值求解,能够得到缸内温度T、缸内压力P、工质质量m等热力状态参数随着曲轴转角的变化规律。
3.2 各热力过程数学模型的建立
发动机的工作过程可以简化分为压缩、燃烧、膨胀、换气等4个阶段,本文研究的模型即是通过这4个过程来对发动机的压力变化进行研究。
3.2.1 压缩阶段
从进气门关闭到混合气开始燃烧,不存在燃料燃烧放热过程,仅仅是对一定质量的气体不断压缩,故存在以下关系:
质量守恒简化为:
能量守恒方程简化为:
压缩阶段模型见图2。
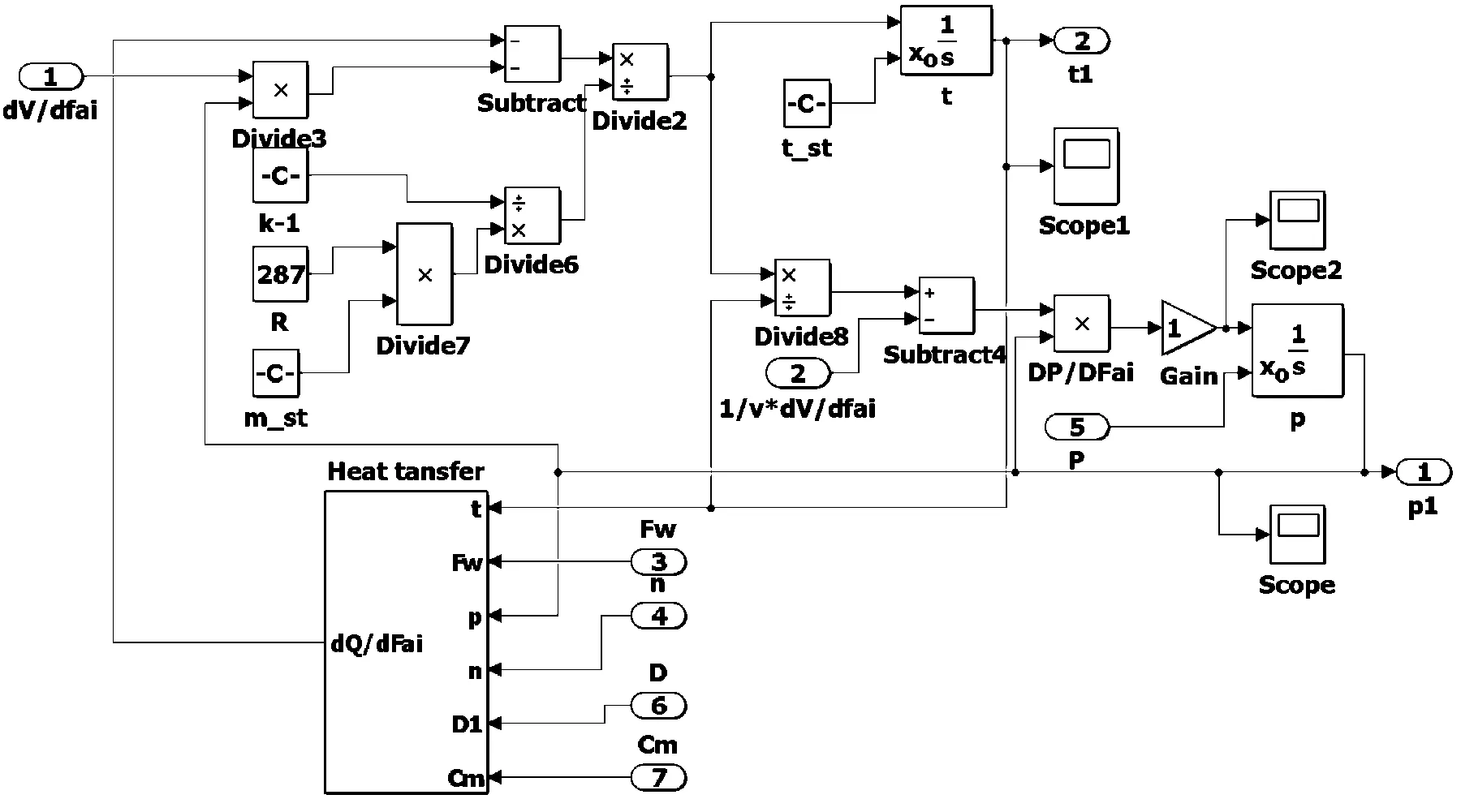
图2 压缩阶段
3.2.2 燃烧阶段
燃烧阶段模型见图3。
3.2.3 膨胀阶段
膨胀阶段由燃烧终点起至排气门开启时刻止。膨胀阶段从燃烧结束一直到排气门打开,与压缩阶段相似。
能量守恒方程简化如下:

图3 燃烧阶段
3.2.4 纯排气阶段
单纯排气阶段从排气门打开开始一直到进气门打开为止。质量守恒方程简化如下:
能量守恒方程简化如下:
(12)
3.2.5 纯进气阶段
单纯进气阶段从排气门关闭一直持续到进气门关闭。
质量守恒方程简化为:
能量守恒方程简化为:
3.2.6 进排气叠开阶段
质量守恒方程:
能量守恒方程:
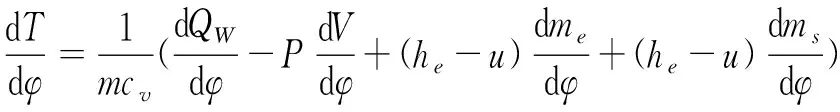
(16)
3.3 边界条件的确定
发动机工作过程中有众多的边界条件有待通过计算获得,例如过量空气系数、汽缸容积等。
3.3.1 过量空气系数
瞬时过量空气系数αφ为实际空气质量mL和燃烧理论上所需的空气量mB的比值:
式中:m为汽缸内工质总质量;mL为汽缸内的实际空气质量;mB为某瞬间前汽缸内已燃烧的燃油质量;L0为理论空气量(L0=14.3 kg)。
瞬时过量空气系数随曲轴转角的变化率为:
3.3.2 瞬时绝热指数kφ和比热C
瞬时绝热指数kφ利用串山公式计算:
kφ=1.437 3-1.318×10-4·T+
3.12×10-8·T2-4.8×10-2/αφ
当R、k求得之后,可以利用热力学公式计算比热(kJ/(kmol·K)):
3.3.3 汽缸工作容积
瞬时汽缸工作容积为
汽缸容积的变化率为

瞬时汽缸容积模型见图4。

图4 瞬时汽缸容积
3.3.4 内能u和焓h
h=u+RT
u=Cv·T
h=Cp·T
(22)
3.3.5 汽缸周壁传热
气体对汽缸周壁的放热率为
其中FW=4V/D为汽缸内壁平均温度。
根据胡希尼(G.Woschni)在1965年提出的公式可得:
KW=265D-0.214(Cmp)0.786T-0.525
(24)
式中Cm为活塞平均速度(Cm=S·n/30)。
3.3.6 燃烧过程的放热规律
发动机的燃烧过程极其复杂,燃烧模型建立的好坏直接影响最终的仿真结果。通用的Vibe燃烧模型由于具有控制参数少、结构简单等优点,在发动机模型计算研究中被广泛应用。
Vibe公式为:

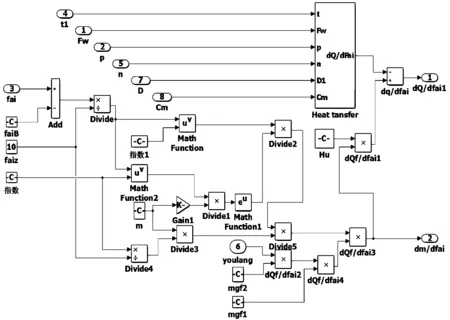
图5 Vibe公式
3.3.7 单个汽缸激振力矩
单个汽缸内气体工作压力对曲轴产生的激振力矩为
式中:Pg为汽缸内工质压力(kg/cm);D为汽缸直径(cm)。
单个汽缸内气体工作压力对曲轴产生的激振力矩模型见图6。

图6 单个汽缸内气体工作压力对曲轴产生的激振力矩
4 模型验证
本文研究的试验数据为模型仿真信号与商业软件AMESim仿真信号的跟踪对比。
发动机扭振模拟试验以某四缸四冲程汽油机为模拟对象,该机型的相关参数如表1所示。图7为汽缸压力产生的激振力矩,图8为模拟信号单个汽缸产生的惯性力矩。通过缸平移法按照点火顺序依次将四缸的单个汽缸压力产生的激振力矩与单个汽缸产生的惯性力矩相叠加,得到最终的发动机扭振模拟信号。

表1 某款直列四缸四冲程汽油发动机参数
在图9~12中,Ten为模拟参考信号,T1为实测扭振信号,均进行了平滑滤波处理。本文从众多数据中挑选了发动机2 000 r/min油门开度分别为50和70与3 000 N/min油门开度分别为70和100四个工况。

图7 汽缸压力产生的激振力矩

图8 单个汽缸产生的惯性力矩曲线

图9 发动机转速为2 000 r/min、油门开度为50%时的扭振曲线对比

图10 发动机转速为2 000 r/min、油门开度为70%时的扭振曲线对比
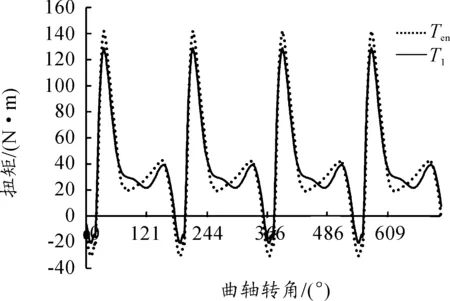
图11 发动机转速为3 000 r/min、油门开度为70%时的扭振曲线对比

图12 发动机转速为3 000 r/min、油门开度为100%时的扭振曲线对比

表2 发动机转速为2 000 r/min、油门开度为70%时Simulink模拟和商业软件AMESim仿真数据分析 N·m

表3 发动机转速为3 000 r/min、油门开度为70%时Simulink模拟和商业软件AMESim仿真数据分析 N·m
与商业软件AMESim仿真信号相比,模拟信号误差较低,精度较高,能有效地反映实测信号的扭振特性,证明在所提供的参数较少的情况下,该发动机高瞬态扭振模型能较为精确地模拟发动机扭转振动特性。
5 结束语
本文以某款四缸四冲程汽油发动机为参考机型,利用Matlab/Simulink建立了一套可以应用于汽车试验台架的发动机高瞬态扭振实时控制模型。仿真与试验对比结果表明:该仿真模型在所提供的参数较少的情况下,能较为精确地模拟发动机扭转振动特性。
本研究所建立的发动机扭振实时控制模型计算量较小,运行速度快,可以满足发动机模拟高动态实时控制的要求,输出信号能为传动系NVH台架与变速器硬件在环试验等试验提供有效激励源。该模型为试验台架动态测试提供了理论基础,对发动机扭振模拟技术的研究有着重要意义。

