微型电动汽车悬架系统设计与平顺性分析
陈 鑫,兰凤崇,陈吉清,翁楚滨,曾文波
(1.华南理工大学 机械与汽车工程学院/广东省汽车工程重点实验室, 广州 510640;2.中国电器科学研究院 工业产品环境适应性国家重点实验室, 广州 510300)
近年来,微型电动汽车逐渐受到一些消费者的青睐,但其也存在着操纵稳定性和平顺性较差、安全得不到保障等问题,这不仅会影响到乘员的乘坐体验,甚至会危及乘员的生命安全。汽车悬架系统作为汽车重要的组成部分,对于确保汽车的舒适性和安全性有着重要意义。国内外关于汽车悬架系统的研究主要围绕以上性能展开,并且多以基准车为基础,针对已有悬架系统以改善性能为目标进行分析和优化。一方面,在已有悬架系统结构基础上进行结构参数化,根据悬架的综合性能要求进行参数协同设计优化。如:马俊等[1]基于转向回正性能和轻便性,计及残留横摆角速度和前轮定位诸参数之间的关系,建立了一种前轮定位参数优化设计方法,并以某轻型货车为例,对其前轮定位参数值进行优化,并通过相关试验验证了所选定位参数的正确性和合理性;刘伟等[2]以汽车行驶平顺性、操纵稳定性为优化目标,对后悬架弹簧刚度、减振器阻尼系数及稳定杆扭转刚度进行了优化。另一方面,从悬架动力学特性出发,在虚拟载荷系统中利用数值分析对系统结构进行改进或设计优化,如梅声远等[3]利用有限元方法对某款乘用车扭转梁半独立后悬架进行了静力分析,获得了在各种典型工况下悬架结构强度分布规律和动态特性,并对原有结构的设计薄弱环节提出了改进方向。
本研究对全新开发的微型电动车进行悬架设计,针对其整车质量小、尺寸小的特点给出该车悬架系统的设计方法,根据整车布置和性能要求进行结构设计,结合结构参数化和有限元数值化方法,对悬架系统进行优化和校核,并通过整车平顺性分析验证悬架系统设计的合理性。
1 悬架系统的参数化
1.1 悬架形式选择
目标车总质量m为700 kg,总簧下质量mu为60 kg,轴荷比为55∶45,轴距L为1 870 mm,轮距B为1 480 mm,前轮型号为145/60R13,后轮型号为165/55R13。该车定位为短距离代步车,设计最高行驶车速为100 km/h,对乘坐舒适性的要求不算很高,且整车尺寸较小,不适合占用空间较多的悬架类型。麦弗逊悬架具有经济性好、结构简单、占用空间小、车轮定位参数变化小等优点,故选择麦弗逊式悬架作为该车的前悬架。扭转梁随动臂式悬架具有结构简单、成本低、适用于前置前驱乘用车后悬架等特点,故选择扭转梁随动臂式悬架作为该车的后悬架。
在设计悬架时,往往以其需要达到的性能作为驱动。悬架系统作为汽车重要的组成部分,对汽车的操纵稳定性和可靠性有着极大的影响。在车轮上下跳动时,车轮定位参数会发生变化,若其变化能满足一定要求,则能使汽车具有较好的操纵稳定性。可靠性涉及零件的耐久性、强度等方面,这里主要考虑后悬架的强度表现。因此,在完成悬架的初步设计后,将就车轮定位参数的变化特性和扭转梁后悬架在极限工况下的强度性能两个方面对悬架系统进行性能分析及优化。
1.2 悬架的设计参数
悬架的设计参数可以归结为两类:表征结构尺寸的硬点坐标和表征力学特性的弹簧刚度及减震器阻尼。悬架的硬点坐标决定了前轮定位参数随车轮跳动时的变化特性,由设计经验选定前轮外倾角和前束角为0°,主销后倾角为3°,主销内倾角为12°,主销偏移距为15 mm。根据上述前轮定位参数初始值和布置要求,绘制了前悬架导向机构,见图1。扭转梁悬架的强度受很多因素影响,如悬架结构和尺寸、加工工艺等,图2为结合整车设计需求和装配要求建立的扭转梁悬架三维模型。
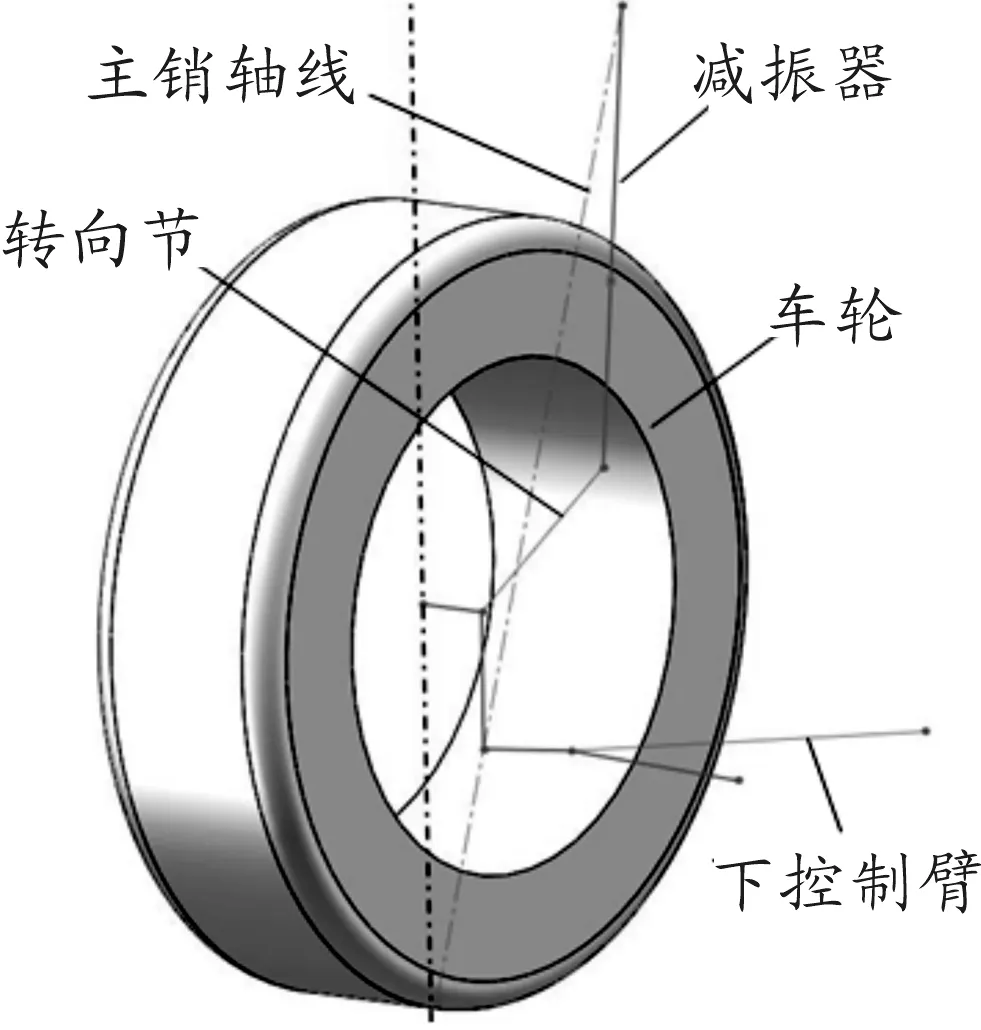
图1 导向机构
由建立的前后悬架模型得到了悬架硬点坐标,如表1所示,并在Adams中建立了悬架系统的仿真模型(见图3、图4)。

图2 后悬架扭转梁结构形式三维模型

图3 麦弗逊悬架系统
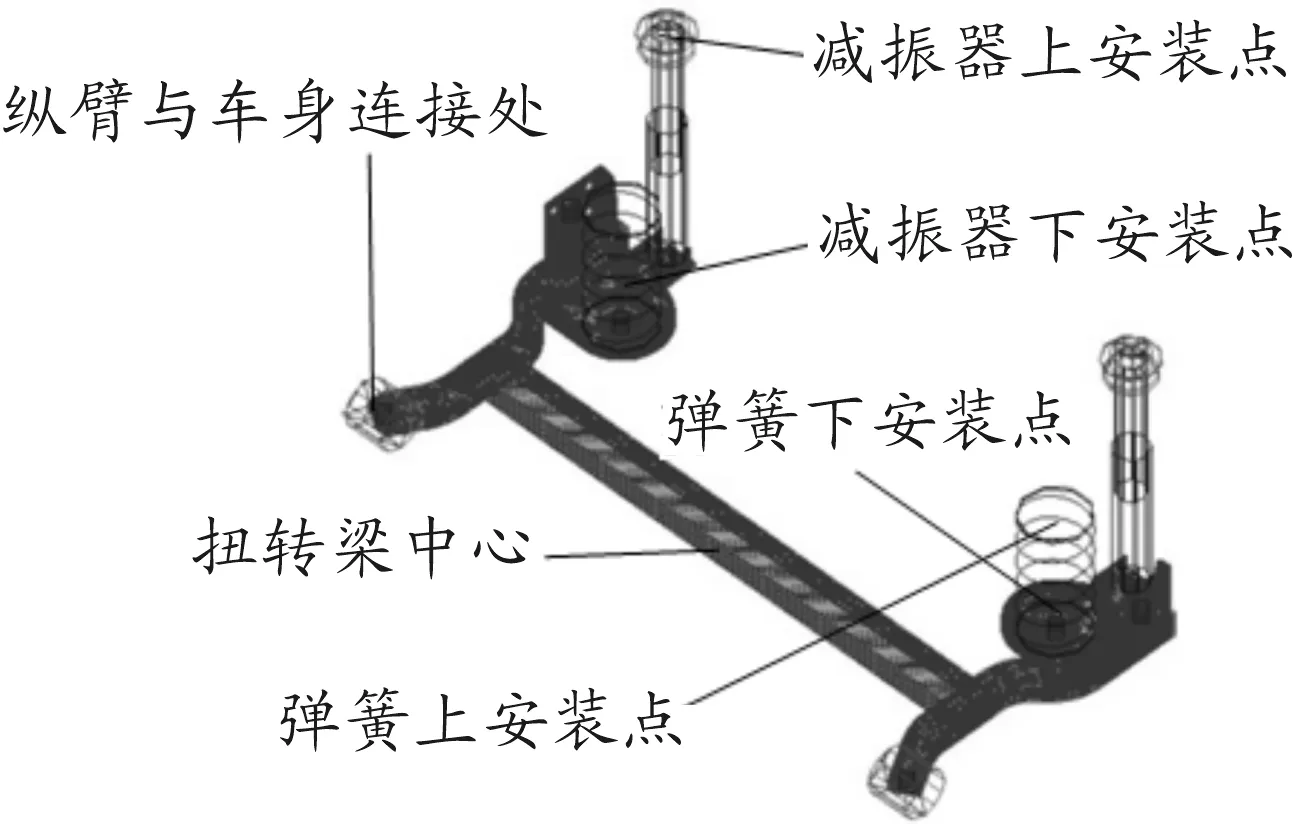
图4 扭转梁悬架系统

表1 悬架硬点坐标
根据整车参数和设计经验,选定:前悬架刚度为21 kN/m,偏频为1.23 Hz,静挠度为164.4 mm;后悬架刚度为22 kN/m,偏频为1.39 Hz,静挠度为128.4 mm。取压缩时相对阻尼系数ζc=0.12,伸张时相对阻尼系数ζe=0.4,可求得前悬架压缩时阻尼为652.5 N·s/m,伸张时阻尼为2 175.1 N·s/m;后悬架压缩时阻尼为604.1 N·s/m,伸张时阻尼为2 013.7N·s/m。如图5所示:Kl和δ分别为麦弗逊悬架单侧的刚度和阻尼,也即悬架总刚度和总阻尼的一半;b为减振器上部安装点A到悬架侧倾中心M的距离;p为轮胎接地点C到悬架侧倾中心M的距离。对于麦弗逊悬架,其弹簧刚度与悬架总刚度,减振器阻尼与悬架总阻尼分别有如式(1)和(2)的数学关系。
由麦弗逊悬架导向机构确定b和p的值分别为3 890.8mm、4 041.6mm,由式(1)和(2)可得前悬架弹簧刚度Ks为11.3kN/m,减振器阻尼δa为352.0N·s/m(压缩时)和1 173.5N·s/m(伸张时)。
2 悬架性能特性分析及优化
2.1 前轮定位参数的变化特性
前轮定位参数随车轮跳动有良好的变化特性,对于汽车的操纵稳定性有着积极的意义。一般要求:在车轮跳动量为±50mm时,前轮外倾角变化范围为0°~1°20′,变化量为-2°~+0.5°/50mm;主销后倾角变化范围为1°~4°;主销内倾角变化范围为11°~15°30′;前束角变化范围为0°±10′,变化量为0°~-0.5°/50mm[4-5]。
为了分析前轮定位参数随车轮跳动的变化特性,在Adams中对前悬架进行双轮同向跳动仿真,结果如图6虚线所示。由图6可见:前轮外倾角变化范围为-0.3°~1.25°,变化量约为1.06°/50mm;主销后倾角变化范围为2.8°~3.35°;主销内倾角变化范围为10°~13.3°;前束角变化范围为-0.025°~0.375°,变化量为0.375°/50mm。因此,除了主销内倾角超出了变化范围需要优化外,其余3个定位参数均满足前述要求。
利用Adams的Insight模块对主销内倾角进行优化,选择主销内倾角的均方根值为优化目标,其值越小越好。考虑到整车装配等因素,诸如减振器下部安装点、车轮中心、弹簧下支座等很难调整,故选择减振器上安装点,下控制臂外点,下控制臂前后点的x、y、z坐标作为优化变量。为了从众多优化变量中筛选出对优化目标影响最大的变量,需要先分析主销内倾角对于各个优化变量的灵敏度。设定各优化变量的变化范围为±1%,仿真时间为 10s,车轮跳动量为±50mm,对模型进行以试验要素筛选为目的的双轮同向跳动仿真,结果如图7所示。
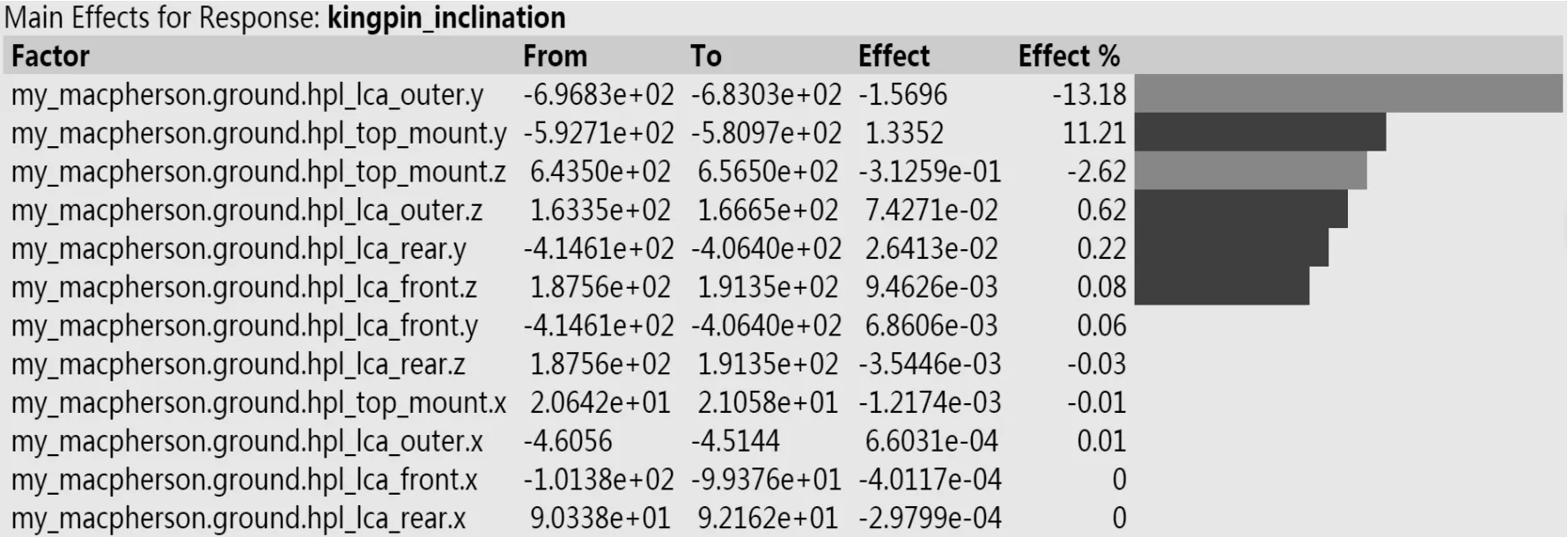
图7 主销内倾角对各变量的敏感度
这里选取对主销内倾角有5%以上灵敏度的变量,即下控制臂外点的y坐标(lca_outer.y)和减振器上部安装点的y坐标(top_mount.y)作为设计变量,将其变化范围约束在±10%内。设置4个定位参数的均方根值处于前述设计要求范围内,作为约束条件。采用二次响应面拟合法优化,其余试验条件与灵敏度分析试验相同。优化后下控制臂外点的y坐标和减振器上部安装点的y坐标分别为-696.83和-581.23。
优化后再次仿真,结果如图6实线所示,可以看到主销内倾角变化范围约为11.5°~14.8°,已经在理想范围内,而前轮外倾角、主销后倾角的变化和之前相差很小。虽然前束角变化相较之前而言,在车轮上跳时增加的趋势更为明显,但最大变化量和变化范围却减少了,更加接近0°。
2.2 多种极限工况下的性能分析
将扭转梁悬架三维模型导入Hypermesh软件后,对各个零件抽取中面,进行几何清理, 然后用2D里的automesh对模型进行网格划分。网格是以四边形为主、有少数三角形的混合单元。用1Drigid单元模拟焊缝,将有装配关系的零件的对应点连接起来。应尽量使较多的对应点连接,且连线要接近水平,以保证受力均匀,避免应力集中或过大。通过移动单元节点、单元自动优化等方法,使模型的QI值(质量指数)达到0.01,表明网格质量很好,无任何单元失效。结构各零件材料都为钢,弹性模量为2.1×105GPa,泊松比为0.3,密度为7.9×103kg/m3,屈服极限为355MPa。横梁的厚度为1.5mm,纵臂和弹簧座的厚度为5mm,轮毂法兰盘和衬套安装处的厚度为6mm。
对于扭转梁后悬架的强度分析,主要考虑以下几种极限工况:双侧车轮驶过凸包、紧急制动和极限转向。先在纵臂与车身连接处,衬套的中心添加节点,再用刚性单元将该节点与衬套安装处的所有节点连接,并约束节点X、Y、Z三个方向的平动自由度和绕Y、Z轴的转动自由度,以此来模拟车身对纵臂的约束。再在弹簧支座加上1D弹簧单元,模拟悬架弹簧。然后根据具体工况的受力情况,在两侧轮毂法兰盘的4个螺栓孔圆周节点上加载相应载荷即可。
驶过凸包工况:车轮经过减速带等不平路面时,路面对车轮有很大的冲击,并会传递给扭转梁悬架。取动载系数k=2,则两侧车轮受到垂向力FZ为
紧急制动工况:急刹车时,车轮接近抱死,除垂直方向的力FZ外,还受到纵向的地面制动力作用,取路面附着系数φ=0.7。
FX=FZφ=989 N
(4)
极限转向工况:极限转向时,车辆受到离心力的作用,转向内侧离开地面,仅靠外侧车轮支撑,同时该侧到地面侧向摩擦力FY的作用。
FZ=2 826 N
FY=FZφ=1 978 N
(5)
仅以3种极限工况中的应力最大的极限转向工况为例,该工况下应力几乎只分布在受力车轮一侧,分析结果如图8所示,由图8可见:最大应力为352 MPa,发生在纵臂与车身连接处,小于材料的屈服极限;最大位移为2.9 mm,发生在轮毂法兰盘外端。因此,设计的扭转梁悬架满足强度要求。

图8 极限转向时的强度校核云图
3 整车平顺性仿真
3.1 随机沥青路面仿真
在前述前后悬架子系统的基础上搭建了整车模型,如图9所示。为了进行平顺性仿真,还需为悬架系统赋予弹簧刚度特性和减振器阻尼特性。在设计经验范围内,对弹簧刚度和减振器阻尼多次取值仿真,得到了较为合适的组合如下:前后悬架的弹簧刚度均为7 kN/m,前后悬架的减振器阻尼均为300 N·s/m(压缩时)和1 200 N·s/m(伸张时)。
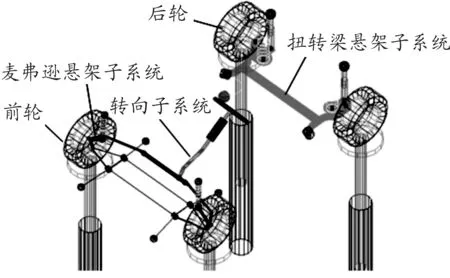
图9 整车仿真模型
Adams自带的路面生成工具以Sayers经验模型为基础,输入不同的功率谱密度,即可得到相应等级的随机路面。选择B级沥青路面进行仿真,对应的Sayers模型空间功率谱密度Ge为0 m2·s,速度功率谱密度Gs为12 m2·s,加速度功率谱密度Ga为0.17 m2·s。以常用车速40 km/h在生成的随机沥青路面上仿真,仿真结果如图10所示。可以看出:车身质心在纵向振动的功率谱峰值出现在2.2 Hz和5.5 Hz处,在侧向振动的功率谱峰值出现在6.8 Hz和17.5 Hz处,避开了水平振动最敏感频率范围0.5~2 Hz,但2.2 Hz与该范围的上限很接近,会使人略微感到不舒适;在垂向振动的功率谱峰值出现在2.6 Hz和18.1 Hz,不处于垂向振动最敏感频率范围4~12.5 Hz。从峰值频率看,本车的平顺性比较好。
3.2 平顺性计算与评估
根据国标和ISO 2631—1:1997(E),单轴向加权加速度均方根值aw可由式(6)求得。
式中W( f )频率加权函数见式(7)和(8),其图像见图11。
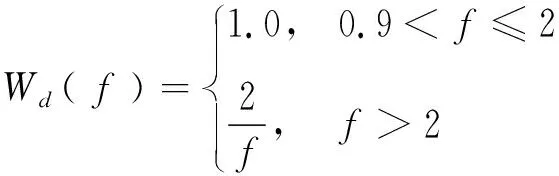
(7)
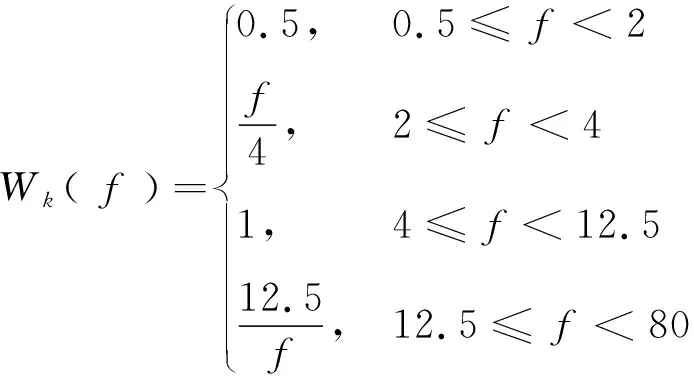
(8)
根据式(6),用加权函数曲线的平方与功率谱密度曲线相乘得曲线1,对其积分得曲线2(图12),其最大值再开方,得车身质心处Z轴向加权加速度均方根值为0.428m/s2。由于座椅下方车身处的垂向加速度均方根值是座椅上人体感受的1.4倍以上[8],故可以用车身质心处3个方向上的加权加速度均方根值除以1.4作为本车平顺性的评价指标。于是计算得Z轴加权加速度均方根值azw为0.306m/s2,用同样的方法求得X轴和Y轴加权加速度均方根值axw、ayw分别为0.010m/s2和0.183m/s2。
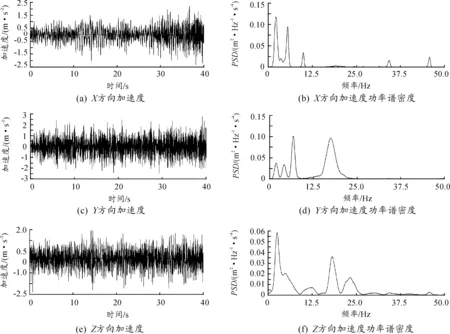
图10 车身质心处3个方向的加速度时间历程及其功率谱密度曲线

图11 频率加权函数
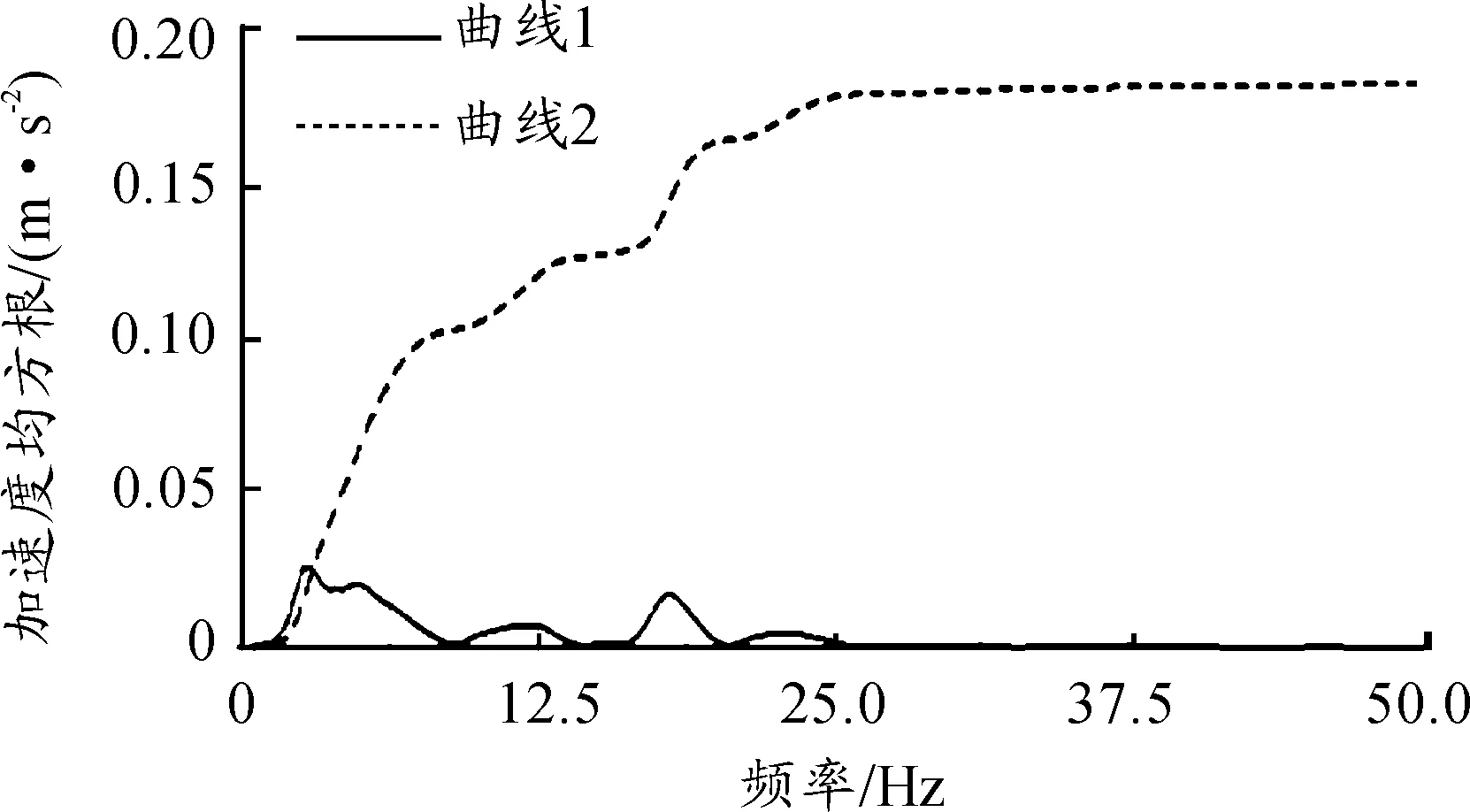
图12 车身质心Z轴加权加速度均方根值
可见,X轴加权加速度均方根值axw几乎为0,这是因为汽车轴距短,且前后悬架匹配较为合理,使得汽车前后部分振动比较一致,没有明显的俯仰运动。Y轴加权加速度均方根值ayw相较而言就比较大,因为在设置仿真参数时,两侧轮辙输入的信号并不完全相同,汽车在行驶时会产生侧倾运动。根据轴加权加速度均方根值ayw与人的主观感觉之间的关系,在X、Y、Z三个方向的加权加速度均方根值均低于0.315m/s2的安全阈值。因此,本车在沥青路面(B级路面)下行驶时的平顺性良好,能带给乘员舒适的乘坐体验。
4 结束语
针对全新开发微型电动车悬架系统设计,为确保汽车具有良好的平顺性、操纵稳定性和可靠性,确定了定位参数优化、强度校核和平顺性评估等流程,能节省微型电动汽车开发时的实车试验成本并缩短研发周期,可作为微型电动汽车悬架设计参考。
悬架系统设计参数为表征悬架结构尺寸的硬点坐标及表征悬架力学特性的弹簧刚度和减振器阻尼。结合整车布置和设计要求,建立了麦弗逊悬架模型和扭转梁悬架模型,确定了上述参数的初始值。
通过双轮跳动仿真,得到了前轮定位参数随车轮跳动的变化曲线。针对主销内倾角变化不够理想的问题进行了优化,结果显示:主销内倾角变化范围从10°~13.3°变为11°~15°30′,并且所有定位参数均有良好的变化特性。分析了极限工况下扭转梁悬架的受力情况,最大应力为352 MPa,小于材料的屈服极限,说明设计的扭转梁悬架满足强度要求。
基于设计的悬架系统建立了整车仿真模型,通过随机沥青路面平顺性仿真得到了汽车在40 km/h时的加权加速度均方根值,该值小于 0.315 m/s2的安全阈值,表明该车的平顺性良好。在保证建立的整车模型与实车高度吻合的前提下,该方法可作为评估汽车平顺性的有效且便捷手段。在利用其他优化方法获得前后悬架弹簧刚度和减振器阻尼的最优解后,修改模型中的相关特性,重新仿真便可以得到最佳的平顺性,从而验证优化结果的正确性,为实车试制时的参数取值提供重要理论依据。

