基于云计算平台的差分进化算法改进研究
孙洁 连畅
摘 要: 针对差分进化算法(DE)收敛速度慢、多样性不足和易陷于局部最优的问题,进行基于云计算的差分进化算法改进研究。该方法基于云对差分算法的运行速度进行改善,并以差分算法与轮盘赌相结合的方式改进差分算法易陷于局部最优的问题,即在交叉变异之后对种群以轮盘赌法的方式对其进行筛选,使之能够更好地对个体进行最优的选择,从而实现全局最优的结果。实验结果表明,算法改进后对基本差分算法的收敛速度慢,易陷入局部最优的缺陷有了进一步的改善,并很好地提高了最优解的质量,具有良好的实用性。
关键词: 差分算法; 云计算; 轮盘赌; 多样性; 全局最优; 交叉变异
中图分类号: TN911.1?34; TP301 文献标识码: A 文章编号: 1004?373X(2018)17?0163?04
Abstract: Since the differential evolution (DE) algorithm has slow convergence speed and poor diversity, and is easy to fall into local optimum, an improved DE algorithm based on cloud computing platform is studied. This method based on cloud platform is used to improve the running speed of the DE algorithm. The DE algorithm and roulette method are combined to improve the problem that the DE algorithm is easy to fall into local optimum, in which the population after cross variation is screened by means of roulette method to select the optimal individual and realize the global optimum. The experimental results show that the improved algorithm can further improve the defects of the basic differential algorithm, greatly improve the quality of the optimal solution, and has high practicability.
Keywords: differential evolution algorithm; cloud computing; roulette; diversity; global optimum; cross variation
0 引 言
云计算云平台中数据的开发和并行一般使用Hadoop平台处理。Hadoop平台由Hadoop分布式文件系统(HDFS)和MapReduce计算模型两个板块构成。运行成本低,具有很强的扩容能力,运算效率高等是Hadoop平台的主要特点。
差分进化算法(Differential Evolution,DE)是近年来众多新兴算法中的一种[1]。最开始DE只用于一种多项式问题的解决,后来发现有关复杂优化的问题也可以用DE研究解决,差分进化算法更是一种群体智能指导的优化搜索。
目前,很多学者也都对DE进行了非常深入的研究,文献[2]提出一种基于反向学习的跨种群的差分进化改进方法,以此提高算法对单峰函数的求解精度和稳定性;文献[3]提出一种基于反省学习的约束差分进化算法,将反向学习的机器学习方法的框架运用到差分进化算法中;文献[4]提出一种改进种群多样性的双变异差分进化算法,通过引入BFS?best机制(基于排序的可行解選取递减策略)对变异算子进行改进;文献[5]采用DE 标准框架,当群体适应值方差小于一定阈值时,引入极值优化算法,提出基于极值优化的混合差分进化算法;文献[6]提出一种基于代理模型的差分进化算法(DESSA),通过对多策略机制的运用实现对单一策略的改进,将多个策略在每一步的进化中进行渗透。虽然上述方法都对差分算法进行了改进,并在不同程度上对算法的收敛速度进行了提高,但收敛精度却普遍不高,且有着使差分进化算法拥有大量的迭代并易陷入局部最优的问题。为了改进这些缺陷,本文通过在差分进化算法中加入轮盘赌的方式对其收敛速度进一步进行改善,改进算法易限于局部最优的问题。
1 云计算
1.1 HDFS分布式文件系统
HDFS分布式文件系统的架构采用主/从(Master/Slave)架。系统一共由NameNode节点、Secondary?NameNode节点和DataNode节点构成,其中NameNode和DataNode分别为系统的主、从节点,主、从节点都以Java程序的形式以Linux为操作系统运行在普通商用计算机上。
1.2 MapRaduce框架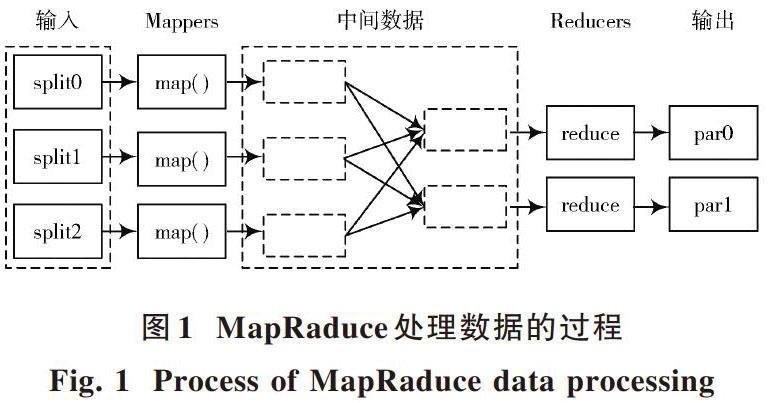
MapRaduce模型一般采用“分而治之”的思想处理大规模的数据集,将所有待处理的大规模数据分割成许许多多的小数据块,所有小数据块经map()函数并行处理后输出新的结果。
将[f]设为最小化适应度函数,参数的候选方案是从适应度函数以实数向量的方式确定,reduce()函数将多任务处理后所得结果进行汇总得到最终结果。MapRaduce框架分为两个阶段,分别为Map阶段和Reduce阶段,并依次自定义为map()函数和reduce()函数,并且这两个函数将数据在数据集中相互转化[7],处理数据过程如图1所示。
2 差分进化算法
差分进化算法通过交叉因子、缩放因子和种群大小3个控制参数实现。差分进化算法不仅具有运算原理简单、易于学习和容易实现的特点,并且其运行结果还具有可靠性、鲁棒性和收敛速度快等优点。
基本差分进化算法大多以候选方案种群为基础,方案由搜索空间对候选方案进行搜索确定,将简单的数学公式与种群中的现有方案相结合进行实现。将原有方案和新方案相互比较,若新方案与原有方案相比有所进化,则接受新方案;反之,则重新开始,重复以上过程。
假设候选方案的输出适应值为一个任意数值,目的是能够找到搜索空间内全部原始方案[p]中存在的方案[m],且方案[m]满足条件[fm 假设[X=x1,x2,…,xn∈Rn]为种群中的一个个体,基本差分进化算法如下所述[8]: 1) 将搜索空间中的所有个体全部初始化。 2) 在种群初始化后的所有个体中,从中随机选择三个不同的个体,设置为[a],[b]和[c]。[R∈1,2,…,n]为被选择的随机索引,并把待优化问题维数设为[n],对每个[i∈1,2,…,n]进行如下迭代计算,可能产生的新个体设为[Y=y1,y2,…,yn], [ri?U0,1]为生成的随机数。如果[i=R]或[ri 3) 重复上述操作直到找到满足最大迭代数或找到满足适应值的个体才会停止。 需要说明的是[F∈0,2]为缩放因子,[CR∈0,1]为交叉因子,种群大小取值[CR>3]。 种群大小[NP]、交叉因子[CR]和缩放因子[F]都决定了差分进化算法优化效果的优良。 3.1 种群规模 实验研究证明,如果种群过小会限制搜索,并且使搜索进入停顿状态,结果将得不到全局最优解,但若种群过大则会产生大量的无效移动,这些大量的无效移动会导致算法的收敛速度减慢。一般情况下全局最优解的概率的搜索会随着种群规模的增大而增大,但是相对应的计算量和计算时间也会随着种群规模的上升而上升,即种群规模的不断增大并非能够不断提高最优解的质量。有时最优解精度降低的原因恰恰是因为种群规模的增加。综上可知,为了有效提高算法的搜索效率,需要对种群规模进行合理取值。 一般当最大进化代数确定,在解决低维简单问题时,若要取得最好的最优解精度,可以将种群规模的取值范围放到[15,35]内,此时不仅最优解的精度高而且也能保持种群多样性和算法收敛速度之间的相对平衡;当解决高维复杂問题时,需要将种群规模的取值放在[30,50]范围内,此时的优化效果较好[9]。 3.2 缩放因子 差分进化算法的优化性能每一个参数都可以控制。特别是缩放因子[F],[F]取值的大小不仅影响算法收敛性的优劣还决定算法收敛速度的快慢。若要收敛速度较快,则[F]需要控制在较小的取值范围内,随着[F]取值的降低,取值越小,越会使种群过早地收敛于非最优解;当[F]取值在较大范围内时,同时对其他参数进行合理的取值,则能保证收敛到问题的最优解,但缺陷是会出现收敛速度较慢的现象。文献[10]对测试函数做了大量的数值模拟实验,研究发现[0.2,0.9]通常为[F]的最佳取值范围。优化问题含有10个以上设计变量时,[F]的最佳取值范围为[0.2,0.6]。由此,文献[11]通过大量的实验研究提出一个方案,此方案较为简单地对缩放因子[F]进行自适应调整,即按式(1)对第[N]代的缩放因子[FN]进行动态调整: 3.3 交叉和变异 对原始种群进行交叉和变异操作的目的是产生不同于原始个体的新个体,产生在原来基础上有所进化的新种群,使原始种群得到不断的进化优化。在变异操作之后,加入新的选择机制,防止交叉操作破坏变异出的优良个体。 3.3.1 轮盘赌法 轮盘赌法是比较常见的随机选择方法中的一种,相似于一种轮盘赌游戏,原理很简单,就是把个体适应度按比例全部转化为选择的概率,即按个体所占总体的比例将圆盘上的区域依次划分,其中个体所占比例越大,在圆盘中所划分的区域就越大,相应地被选中的机会也就越大。每转动一次圆盘,在其停止后指针所指向的扇形区域为选中区域,所选中的区域对应的个体即为被选中的个体。轮盘赌法的运行过程如下: 首先对问题中的[n]个位串分别编号,其次对个体所占总体比例的概率进行计算,按照概率的大小对编号依次排序,由此可以改进轮盘赌程序的运行效率。分别计算所有的累计概率,并对其进行统计,统计情况如图2所示,累计概率的序列为[0,0.1,0.3,0.35,…]。利用rand函数产生一个[0,1] 之间的随机数,并判断此随机数在累计概率序列中的位置,选择其在序列值中所能大于的最大值[m],即需要大于前一个累计概率并小于下一个累计概率,就是对[m]号位串进行随机选择[12]。例如,假设图2中产生的随机数为0.12,选择0.12在序列值中所能大于的最大值0.1,且小于下一个累计概率0.3,所以2号位串被选中。 3.3.2 交叉和变异 差分进化算法每进化一代会产生新的进化种群,对进化后的种群实施交叉变异操作,使得种群中的个体产生变异优化的结果,分别选出产生新个体中最优秀的个体和原始种群中最优秀的个体,将两个最优个体相比较,若产生的新的个体更优秀,则代替原有个体进行下一代进化,若不能产生更优秀的个体,则进行下一次进化。3 差分进化算法的改进


4 实例仿真
本节实验在Linux环境下建立Hadoop 2.0集群环境,实验集群由4个节点组成,使用4台普通联想PC机,其中1台服务器用来管理其他工作节点,作为HDFS的主控制节点(Master),另外3台PC机用来完成MapReduce任务,作为HDFS的工作节点(Slave)。软件环境使用Linux为操作系统,Hadoop作为云计算平台,编程环境涉及eclipse以及JDK。用改进的差分进化算法进行仿真实验,初始实验参数设置如下:最大迭代次数为1 000,种群大小为40,缩放因子[FN=0.2+rand0,1×0.4],交叉概率为0.9,变异概率为0.5。各函数进化曲线如图4,图5所示。
由于两种算法初始种群随机产生,为了避免算法受一次随机实验的影响,分别对算法重复实验50次,在得到最优解的前提下结果如表1所示。图4,图5相比较可以看到,改进后的差分进化算法较原始差分算法迭代次数少,收敛速度快,说明本文改进的DE算法进一步提高了算法性能。
5 结 论
本文提出基于云计算平台的差分进化算法改进研究的新思路,并将轮盘赌法与差分进化算法相结合,从而改进差分进化算法,具有良好的可操作性。实例仿真证明新的改进对全局优化性能进行了改善,提高了收敛速度和收敛精度,使优化速度获得了一定程度的提高,有效地克服了基本差分算法收敛速度慢、易陷于局部最优的缺陷,在减少迭代次数的同时,进一步提高了最优解的质量。
参考文献
[1] 魏玉霞.差分进化算法的改进及其应用[D].广州:华南理工大学,2013.
WEI Yuxia. Improvement and application of differential evolution algorithm [D]. Guangzhou: South China University of Technology, 2013.
[2] 张斌,李延晖,郭昊.基于反向学习的跨种群差分进化算法[J].计算机应用,2017,37(4):1093?1099.
ZHANG Bin, LI Yanhui, GUO Hao. Cross species differential evolution algorithm based on reverse learning [J]. Journal of computer applications, 2017, 37(4): 1093?1099.
[3] 魏文红,周建龙,陶铭,等.一种基于反向学习的约束差分进化算法[J].电子学报,2016,44(2):426?436.
WEI Wenhong, ZHOU Jianlong, TAO Ming, et al. A constrained differential evolution algorithm based on reverse lear?ning [J]. Acta electronica Sinica, 2016, 44(2): 426?436.
[4] 李荣雨,陈庆倩,陈菲尔.改进种群多样性的双变异差分进化算法[J].运筹学学报,2017,21(1):44?54.
LI Rongyu, CHEN Qingqian, CHEN Feier. Double mutation differential evolution algorithm for improving population diversity [J]. Operations research transactions, 2017, 21(1): 44?54.
[5] 王丛佼,王锡淮,肖建梅.基于极值优化的混合差分进化算法[J].计算机科学,2013,40(5):257?260.
WANG Congjiao, WANG Xihuai, XIAO Jianmei. Hybrid differential evolution algorithm based on extremum optimization [J]. Computer science, 2013, 40(5): 257?260.
[6] LU X, TANG K, SENDHOFF B, et al. A new self?adaptation scheme for differential evolution [J]. Neurocomputing, 2014, 146(C): 2?16.
[7] BARBIERU C, POP F. Soft real?time Hadoop scheduler for big data processing in smart cities [C]// 2016 IEEE International Conference on Advanced Information Networking and Applications. Crans?Montana: IEEE, 2016: 863?870.
[8] 郭鹏.差分进化算法改进研究[D].天津:天津大学,2012.
GUO Peng. Improvement of differential evolution algorithm [D]. Tianjin: Tianjin University, 2012.
[9] 王旭,赵曙光.解决高维优化问题的差分进化算法[J].计算机应用,2014,34(1):179?181.
WANG Xu, ZHAO Shuguang. Differential evolution algorithm for solving high dimensional optimization problems [J]. Journal of computer applications, 2014, 34(1): 179?181.
[10] 袁俊刚,孙治国,曲广吉.差异演化算法的数值模拟研究[J].系统仿真学报,2007,19(20):4646?4648.
YUAN Jungang, SUN Zhiguo, QU Guangji. Numerical simulation of differential evolution algorithm [J]. Journal of system simulation, 2007, 19(20): 4646?4648.
[11] 许小健,黄小平,钱德玲.自适应加速差分进化算法[J].复杂系统与复杂性科学,2008,5(1):87?92.
XU Xiaojian, HUANG Xiaoping, QIAN Deling. Adaptive accelerating differential evolution algorithm [J]. Complex system and complexity science, 2008, 5(1): 87?92.
[12] LIPOWSKI A, LIPOWSKA D. Roulette?wheel selection via stochastic acceptance [J]. Physica A: statistical mechanics & its applications, 2012, 391(6): 2193?2196.
[13] WU G, MALLIPEDDI R, SUGANTHAN P N, et al. Differential evolution with multi?population based ensemble of mutation strategies [J]. Information sciences, 2016, 329(C): 329?345.

