基于矩形覆盖的异步航迹抗差关联算法
郑麟 衣晓 张怀巍 高玉章
摘 要: 在分布式多目标跟踪系统中,由于各传感器开机时间不同以及采样频率的差异等原因,导致各节点接收到的局部航迹往往是异步不等速率的;同时,系统误差的存在也影响了融合系统的性能。针对这一问题,提出一种基于矩形覆盖的异步航迹抗差关联算法,该算法通过矩形覆盖法生成带差灰区间,然后通过划分区实混合序列与矩形覆盖的方法处理航迹,最后通过灰关联方法进行关联判定。仿真实验表明,本算法能有效解决异步带差航迹的关联问题。
关键词: 异步不等速率航迹; 系统误差; 灰关联; 矩形覆盖; 目标跟踪; 信息融合
中图分类号: TN911.1?34 文献标识码: A 文章编号: 1004?373X(2018)17?0006?05
Abstract: In the distributed multi?target tracking system, the local track received by each node is often asynchronous and has unequal rate due to the different boot time and different sampling frequencies, and the error existing in the system also affects the performance of the fusion system. For the above problems, an asynchronous anti?bias track association algorithm based on rectangular cover method (RCM) is presented. The algorithm generates the difference gray section by means of RCM, and then processes the track by means of the divided interval?real mixed sequence and RCM. The grey correlation method is adopted to judge the correlation of the track. The simulation experimental result shows that the presented algorithm can effectively solve the association problem of asynchronous difference track.
Keywords: asynchronous unequal?rate track; system error; grey correlation; rectangular cover; target tracking; information fusion
0 引 言
在分布式多目标跟踪系统中,由于传感器的采样开始基准、采样频率不尽相同,导致融合中心接收到局部节点的航迹往往是异步不等速率的[1?3],同时,各传感器本身携带的系统误差也增加了目标跟踪的难度。因此,解决系统误差存在下的异步航迹关联问题对分布式多目标跟踪融合有着重要的意义[4]。
对于异步航迹关联问题,目前主要采用的方法是先通过时域配准,再利用内插外推的方法[5]得到等长的航迹序列进行关联。但在时域配准过程中,同步化会导致航迹估计值误差的扩散和传播,并且这种误差难以描述和消除;且大多数研究都是在不考虑系统误差的情况下进行。文献[6]给出无需时域配准的异步航迹关联算法,通过区实序列混合来划分灰区间,关联成功率大大提高,但仍未考虑带差航迹的关联问题。
针对系统误差存在时对异步航迹关联性能的影响问题,本文结合文献[7]提出的矩形投影法,对文献[6]算法进行改进。通过矩形覆盖生成灰区间描述系统误差,显著提高其抗差性能,并且无需时域配准,有效进行异步航迹的关联。
1 模型描述
2 算法描述
2.1 系统误差的描述方法
如图1,在二维笛卡尔坐标系中,传感器[a]的坐标记为原点,测距和测方位角偏差分别为[(Δr1,Δθ1)],[ma]是[k]时刻传感器[a]探测到点的测量位置,其坐标在极坐标下的表示形式为[(r1,θ1)];[ma]为根据最大系统偏差反推出的目标真值最远位置,则图1中阴影部分即为目标真值可能出现的位置区域,称为目标灰区域。由于该区域在坐标轴上的投影是两个相互正交的闭区间,因此可用端点数据对该区间进行描述[7]:
2.2 航迹序列区间化
在某一特定的融合周期[kT,k+1T]内,将第[i]个目标在传感器[a]和[b]下的航迹[Γiaak]和[Γibbk]按照文献[6]中的区实混合序列描述法进行划分,使得划分后的区间数相同且一一对应。具体规则如下:
1) 长度相同原则,即确保将航迹数据变换为统一的长度。一个可行的方案是:选取长度[L=INTunan0],[n0=INTunanb],其中[INTux]为取大于[x]的最小整数运算。
2) 对称性原则,即令每条航迹中生成的区间灰数呈中心对称分布。
3) 在满足条件1)和2)的前提下,尽可能减少新生成的航迹序列中相同时刻点和点对应的情况。
4) 原则的优先级排序:1)[>]2)[>]3)。
3 仿真分析
假设有两部异地配置的2D雷达,坐标分别是(0,0)和(100 km,0)。对50个机动目标跟踪20 s,进行100次Monte Carlo实验。雷达2与雷达1的开机时间相差0.1 s,采样比为3[∶]5,融合中心的采样时间间隔[T=]1 s;采用匀速运动模型,航向和目标速度分别在[0~2π] rad和200~400 m/s之间随机分布,且具有可以认为在速度上变化的过程噪声,两雷达均具有50 m、测角0.5[°]的随机测量误差。目标的初始位置在20 km[×]20 km的矩形位置中随机产生;假设两雷达通信环境均较为理想,传输过程中不存在传输时延现象。图5是两雷达最大系统偏差分别为1 500 m,1.5[°]和-1 500 m,-1.5[°]的环境下,一次仿真实验中某10批目标的真实航迹与雷达上报航迹示意图。
图7,图8分别给出了当系统最大偏差距离、最大偏差角度改变时,本文算法正确关联率的变化趋势。可以看出,在小偏差环境下(2 km,1.5[°])算法具有较高的准确率(80%以上),偏差环境较大时正确关联率下降较快,且受角度影响比距离更明显。由于在大偏差环境下,系统处于过灰化状态,灰度增量显著增加,导致航迹关联准确率明显下降。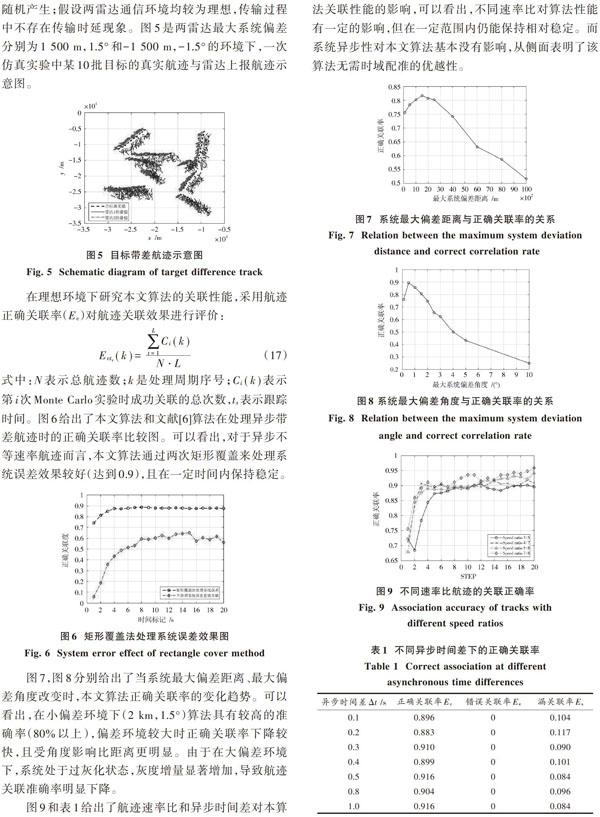
图9和表1给出了航迹速率比和异步时间差对本算法关联性能的影响,可以看出,不同速率比对算法性能有一定的影响,但在一定范围内仍能保持相对稳定。而系统异步性对本文算法基本没有影响,从侧面表明了该算法无需时域配准的优越性。
4 结 语
本文针对分布式多目标跟踪系统中存在的异步带差航迹问题,研究一种无需时域配准的异步不等速率航迹灰关联抗差算法,通过矩形覆盖法与灰区间划分,将异步不等速率航迹转化为相同数量的灰区间进行关联,并通过Monte Carlo仿真实验,对关联性能的影响因素进行探究。仿真结果表明,大多数情况下,本文算法能有效解决异步带差航迹的关联问题。
参考文献
[1] 何友,王国宏,关欣,等.信息融合理论及应用[M].北京:电子工业出版社,2010.
HE Y, WANG G H, GUAN X, et al. Information fusion theory with applications [M]. Beijing: Publishing House of Electronics Industry, 2010.
[2] 韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].北京:清华大学出版社,2006:9?12.
HAN C Z, ZHU H Y, DUAN Z S, et al. Multi?source information fusion [M]. Beijing: Tsinghua University Press, 2006: 9?12.
[3] 潘泉,梁彦,杨峰,等.现代目标跟踪与信息融合[M].北京:国防工业出版社,2009:1?23.
PAN Q, LIANG Y, YANG F, et al. Modern target tracking and information fusion [M]. Beijing: National Defense Industry Press, 2009: 1?23.
[4] ZHU H Y, HAN C Z, HAN H. Asynchronous track?to?track association method in distributed multi?sensor information fusion system [J]. Control theory and applications, 2004(3): 453?456.
[5] ALOUANI A T, RICE T R. On asynchronous data fusion [C]// Proceedings of the Annual Southeastern Symposium on System Theory. Athens: IEEE, 1994: 140?148.
[6] 衣晓,韩健越,张怀巍,等.基于区实混合序列相似度的异步不等速率航迹关联算法[J].航空学报,2015,36(4):1212?1220.
YI Xiao, HAN Jianyue, ZHANG Huaiwei, et al. Asynchronous unequal rate track association algorithm based on the similarity degree of mixed sequences [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1212?1220.
[7] 衣晓,张怀巍,曹昕莹,等.基于区间灰数的分布式多目标航迹关联算法[J].航空学报,2013,34(2):352?360.
YI Xiao, ZHANG Huaiwei, CAO Xinying, et al. Distributed multi?target track association algorithm based on interval ash number [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 352?360.
[8] GUAN X, HE Y, YI X. Grey track?to?track correlation algorithm for distributed multi?target tracking system [J]. Signal processing, 2006, 86(11): 3448?3455.
[9] HAO M, YUAN X, HAN C. Recursive joint track?to?track association and sensor nonlinear bias estimation based on genera?lized Bayes risk [C]// Proceedings of 2015 International Confe?rence on Information Fusion. Washington, DC: IEEE, 2015: 1519?1525.
[10] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:158?164.
DENG Julong. Grey theory basis [M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 158?164.
[11] YI X, HAN J, GUAN X. An asynchronous track?to?track association algorithm without time alignment [J]. Procedia engineering, 2015, 99(35): 1120?1125.

