基于可变仰角阈值的低轨道量子卫星切换策略及性能分析

聂敏 车俊丽 杨光 裴昌幸

摘 要： 为了解决低轨道量子卫星之间的切换问题，根据量子卫星和地面站的连线与水平面之间夹角即仰角的变化，通过对该仰角的实际测量，提出基于可变仰角阈值的低轨道量子卫星切换策略。在达到最小仰角阈值时，地面服务中心发出切换指令，将对地服务卫星切换到下一颗量子卫星，使得星地量子通信保持连续。在此根据仰角大小的不同，分析仰角对卫星通信中量子态生存函数、信道误码率及信道容量的影响，建立它们之间的定量关系。仿真结果表明，当仰角[θ=20°]和[θ=70°]时，自由空间量子态生存函数、信道误码率及信道容量分别为0.56，0.033，0.5和0.92，0.012，0.97，由此可见，仰角大小对量子卫星通信性能有显著的影响。因此，为了保证卫星切换的成功率，根据对不同通信性能的要求，应自适应调整卫星的仰角阈值。

关键词： 低轨道量子卫星； 仰角测量； 卫星切换； 量子通信； 信道容量； 生存函数

中图分类号： TN927?34 文献标识码： A 文章编号： 1004?373X（2018）17?0001?05

Abstract： According to the change of the included angle （elevation angle） between the line connecting the satellite with ground station and horizontal plane， a low orbit quantum satellite handover strategy based on variable elevation angle threshold is proposed by means of the actual measurement of the elevation angle to solve the handover problem between low orbit quantum satellites. When the elevation angle threshold reaches the minimum value， the handover instruction is sent from the ground service center to switch the serving?ground satellite to the next quantum satellite， which makes the satellite?ground quantum communication continuous. According to the different elevation angles， the influence of elevation angle on the quantum state survival function， channel bit error rate and channel capacity in satellite communication is analyzed， and the quantitative relationship among them is established. The simulation results show that， as the elevation angle [θ=20°]， the free space quantum state survival function， channel bit error rate and channel capacity are 0.56， 0.033， 0.5 respectively； as the elevation angle [θ=70°]， the free space quantum state survival function， channel bit error rate and channel capacity are 0.92， 0.012， 0.97 respectively， which shows that the elevation angle has a significant effect on quantum satellite communication performance. The elevation angle threshold of the satellite should be adjusted adaptively according to the requirements of different communication performances to ensure the success rate of satellite handover.

Keywords： low orbit quantum satellite； elevation angle measurement； satellite handover； quantum communication； channel capacity； survival function

0 引 言

随着科学技术的发展，人们对通信质量的要求越来越高，传统卫星通信由于其开放式无线接口使得通信的安全性和保密性得不到有效保障，而量子不可克隆定理和测不准原理使量子通信具有绝对的安全保密性。2012年，中国科技大学潘建伟、彭承志团队在青海湖完成了国际上第一个百公里量级自由空间量子隐形传态和纠缠分发实验[1]，为自由空间量子通信建立了基础；2013年，潘建伟科研小组又利用百公里地面自由空间来模拟星地之间高度衰减的链路信道，完成了星地量子通信地基验证试验[2]，成功验证了量子卫星与地面之间通信的可行性。2016年8月16日1时40分，在酒泉卫星发射中心成功将世界首颗量子科学实验卫星“墨子号”发射成功。随着“墨子号”的成功发射，标志着我国量子科研又迈出了重要一步。

低轨道量子卫星通信[3?5]是实现全球远距离量子通信的关键技术之一，欧、美、日等国已将量子通信列为国家的重点研究项目[6]。由于低轨道卫星对地面站的服务时间有限，如果移动台通信时间较长或通信双方距离较远，就需要进行量子卫星切换技术，而量子切换技术的关键是量子纠缠切换[7?10]。文献[4]提出基于纠缠度计算的低轨道量子卫星通信切换算法，该算法根据纠缠度的大小，选择纠缠度大的卫星进行切换，使切换成功率达到95%以上。文献[5]提出低轨卫星通信接入与切换策略研究，根据不同的地理环境和人口密度，对不同地区的最小仰角进行设置，使得呼叫阻塞率和强制中断率得到显著改善。

本文针对低轨道量子卫星通信进行星上交换技术的研究，在文献[3]和文献[4]的基础上提出最大仰角准则，根据最大仰角准则，分析低轨道量子卫星之间的切换策略；讨论仰角对自由空间量子通信的误码率、信道容量和量子态生存函数的影响，并进行仿真验证，最终得出它们之间的定量关系，为量子卫星的高效切换提供参照依据。

1 量子卫星切换策略

2 星上交换过程

相对于不能建立通信而言，人们更无法忍受通信质量差和通信突然中断的情况，所以对于切换卫星的选择尤为重要，如图4所示。

根据卫星的切换策略，选择Ⅱ号卫星作为地面站A的当前服务卫星，而Ⅰ号卫星仍为地面站B服务。若Alice在地面站A的服务区内，Bob在地面站B的服务区内，此时Ⅰ号卫星发出纠缠光子对1、2，Ⅱ号卫星发出纠缠光子对3、4，分别将1、4号光子发送给地面站，2、3号光子发送给贝尔测量中心进行贝尔测量，使得2、3号光子产生纠缠，从而使得Alice和Bob可以保持通信。若Alice和Bob相距更远，需[n]个卫星进行切换，这种方法同样适用。

3 仰角对量子卫星通信性能的影响

由于云、雾、雨都发生在对流层，而大部分的固体杂质、尘埃颗粒也存在于对流层，因此本文只对对流层进行分析。在能见度一定的情况下，分析仰角大小对量子卫星通信性能的影响，以便在进行卫星切换时根据不同天气情况进行综合考虑，使得卫星的切换更加安全高效。

3.1 仰角对量子卫星通信信道误码率的影响

从图5中可以看出，随着仰角的不断增大，误码率不断减小。当仰角[θ<45°]时，误码率快速减小；而当仰角[θ>45°]时，误码率的改变趋势逐渐平缓，并不断趋于平稳。可见，在小仰角时，仰角对误码率的影响非常显著。因此，在进行卫星切换同时要求误码率的条件下，可对切换时量子卫星的仰角大小进行适当调整。

3.2 仰角对量子卫星通信信道容量的影响

设自由空间环境量子态为[eI]，由于辐射场真空涨落经过一段时间后，量子位以概率[p]从[1]态跃迁到[0]态，自由空间量子态以概率[p]由真空态跃迁到有一个光子的状态[eX]，这个过程可以作用到量子位与环境组成的复合系统上的幺正演化表示如下[14]：

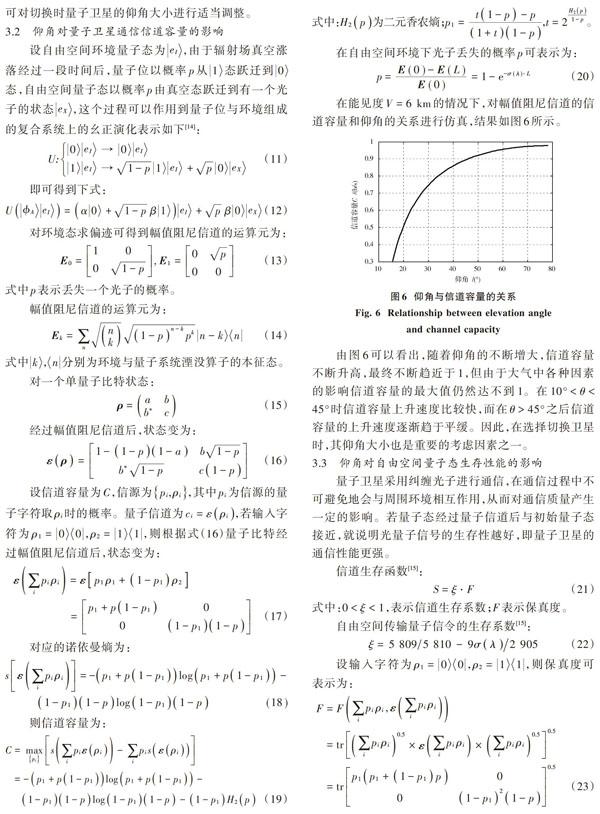
由图6可以看出，随着仰角的不断增大，信道容量不断升高，最终不断趋近于1，但由于大气中各种因素的影响信道容量的最大值仍然达不到1。在[10°<θ<45°]时信道容量上升速度比较快，而在[θ>45°]之后信道容量的上升速度逐渐趋于平缓。因此，在选择切换卫星时，其仰角大小也是重要的考虑因素之一。

3.3 仰角对自由空间量子态生存性能的影响

量子卫星采用纠缠光子进行通信，在通信过程中不可避免地会与周围环境相互作用，从而对通信质量产生一定的影响。若量子态经过量子信道后与初始量子态接近，就说明光量子信号的生存性越好，即量子卫星的通信性能更强。

由图7可以看出，在[p1=0.5]的情况下，信道生存函数和仰角大小的关系为：在仰角[θ<25°]时，信道生存函数基本平稳不变；而在仰角[θ>25°]之后，信道生存函数快速升高，并不断趋近于1。由此可见，随着仰角的不断增大，量子态的生存性能越来越好。因此在进行量子卫星通信时，仰角问题也不容忽视。

4 结 语

本文提出基于可变仰角阈值的低轨道量子卫星切换策略及性能分析。根据仰角的大小确定目的卫星，同时研究了仰角对信道误码率、信道容量及量子态生存函数的影响。仿真结果表明，随着仰角的增大，自由空间量子通信的各种性能指标均受到不同程度的影响。因此，在自由空间量子通信中，除了各种环境因素外，仰角对通信质量的影响也不容忽视，需根据具体的能见度情况，自适应地调整系统参数，以降低背景噪声对量子卫星通信性能的影响。

参考文献

[1] YIN J， REN J G， LU H， et al. Quantum teleportation and entanglement distribution over 100?kilometre free?space channels [J]. Nature， 2012， 488： 185?188.

[2] WANG J Y， YANG B， LIAO S K， et al. Direct and full?scale experimental verifications towards ground?satellite quantum key distribution [J]. Nature photonics， 2013， 7（5）： 387?393.

[3] 王志，聂敏.低轨道量子卫星通信星上交换算法及仿真[J].光子学报，2012，41（9）：1108?1112.

WANG Zhi， NIE Min. Algorithm and simulation onboard switching in low earth orbit quantum satellite communication [J]. Acta photonica Sinica， 2012， 41（9）： 1108?1112.

[4] 张琳，聂敏.基于纠缠度计算的低轨道量子卫星通信切换算法[J].量子电子学报，2013，30（5）：559?565.

ZHANG Lin， NIE Min. Handover algorithm of quantum satellite communication in low earth orbit based on entanglement degree computing [J]. Chinese journal of quantum electronics， 2013， 30（5）： 559?565.

[5] 黄飞.低轨卫星通信接入与切换策略研究[D].成都：电子科技大学，2009.

HUANG Fei. Study on low?orbit satellite communication access and handover strategy [D]. Chengdu： UESTC， 2009.

[6] 贺小云，易运晖.基于逻辑承载网的量子通信网路由和交换策略[J].现代电子技术，2015，38（4）：13?15.

HE Xiaoyun， YI Yunhui. Routing and exchange strategy of quantum communication network based on logic carrying network [J]. Modern electronics technique， 2015， 38（4）： 13?15.

[7] 裴昌幸，阎毅，刘丹，等.一种基于纠缠态的量子中继通信系统[J].光子学报，2008，37（12）：2422?2426.

PEI Changxing， YAN Yi， LIU Dan， et al. A quantum repeater communication system based on entanglement [J]. Acta photonica Sinica， 2008， 37（12）： 2422?2426.

[8] 许敏，聂敏，杨光，等.一种全新的基于纠缠交换的量子中继策略[J].电信科学，2016，32（3）：68?74.

XU Min， NIE Min， YANG Guang， et al. A brand new strategy of quantum relay strategy based on entanglement swapping [J]. Telecommunications science， 2016， 32（3）： 68?74.

[9] 易运晖，聂敏，裴昌幸.基于纠缠交换的多级量子信令传输策略[J].西北大学学报（自然科学版），2012，42（2）：207?211.

YI Yunhui， NIE Min， PEI Changxing. Multi?stage quantum signaling transmission strategy based on entanglement switch [J]. Journal of Northwest University （natural science edition）， 2012， 42（2）： 207?211.

[10] 王剑，陈皇卿，张权，等.基于纠缠交换的量子安全通信协议[J].国防科技大学学报，2007，29（2）：56?60.

WANG Jian， CHEN Huangqing， ZHANG Quan， et al. Quantum secure communication protocols on the basis of entanglement swapping [J]. Journal of National University of Defense Technology， 2007， 29（2）： 56?60.

[11] 尹浩，韩阳.量子通信原理与技术[M].北京：电子工业出版社，2013：43?55.

YIN Hao， HAN Yang. Principle and technology of quantum communication [M]. Beijing： Electronic Industry Press， 2013： 43?55.

[12] 马晶，张光宇，谭立英.基于泊松分布单光子源的量子误码率的分析[J].光学技术，2006，32（1）：101?104.

MA Jing， ZHANG Guangyu， TAN Liying. Analysis of quantum bit error rate based on single?photon source with Poisson distribution [J]. Optical technique， 2006， 32（1）： 101?104.

[13] 张光宇，于思源，马晶，等.背景光对星地量子密钥分配量子误码率的影响[J].光电工程，2007，34（2）：126?129.

ZHANG Guangyu， YU Siyuan， MA Jing， et al. Influence of background light on quantum bit error rate in satellite?to?ground quantum key distribution [J]. Opt?electronic enginee?ring， 2007， 34（2）： 126?129.

[14] 尹浩，马怀新.军事量子通信概论[M].北京：军事科学出版社，2006：267?271.

YIN Hao， MA Huaixin. Introduction of military quantum communication [M]. Beijing： Military Science Press， 2006： 267?271.

[15] 张琳，聂敏，刘晓慧.有噪量子信道生存函数研究及其仿真[J].物理学报，2013，62（15）：24?30.

ZHANG Lin， NIE Min， LIU Xiaohui. Study on survival function of noise quantum channel and its simulation [J]. Acta physica Sinica， 2013， 62（15）： 24?30.