加筋堆石料的动力残余变形特性
何 亮,景宏彬,李国英
(1. 常州工学院,江苏常州 213032; 2. 南京水利科学研究院,江苏南京 210029; 3. 陕西省水务集团有限公司,陕西西安 710068)
高土石坝遭受强震作用时,坝顶部往复地震惯性力可能会导致坝顶区域的堆石料松动,危及大坝安全。坝顶加筋是一种有效的高土石坝抗震加固措施,近年来得到了广泛应用,如高125m的治勒沥青混凝土心墙堆石坝、高108m的水牛家心墙堆石坝、高168m的瀑布沟心墙堆石坝等[1]。当坝顶堆石料发生侧向变形时,依靠筋材与堆石料之间的摩擦和咬合作用传递拉应力,可改善堆石料的力学和变形特性,从而以较小的经济代价获得更大的坝体抗震安全度。
加筋前后堆石料等粗粒土的力学和变形特性均可采用静动力大三轴试验揭示[2-5]。在静力大三轴试验方面,黄仙枝等[6]认为加筋碎石土的强度变化规律服从“准黏聚力”原理,试验围压对加筋效果的影响较大。徐望国等[7]研究表明加筋粗粒土的加筋效应随着轴向应变增大而逐渐发挥,随着加筋层数的增加均有不同程度的提高,加筋前后填料的内摩擦角基本不变,黏聚力增大。傅华等[8]研究表明加筋材料、加筋层数和试样密实度均会显著影响加筋的效果。
在动力大三轴试验方面,邹德高等[9]研究表明加筋可抑制砂砾料的残余剪切变形和残余体积变形。加筋前后的砂砾料永久变形特性均可采用改进的沈珠江模型描述,加筋后的模型参数明显降低。刘汉龙等[10]探讨了围压、循环荷载条件及加筋间距对加筋堆石料动残余变形的影响,认为加筋后堆石料的残余变形变小,且随加筋层数增加残余变形的降低愈明显。
本文基于加筋堆石料的动三轴试验结果,分析加筋前后堆石料的残余变形变化规律,研究加筋层数、围压、筋材网孔大小等对试验结果的影响,并构建了能反映加筋堆石料残余应变与振次关系的经验式。
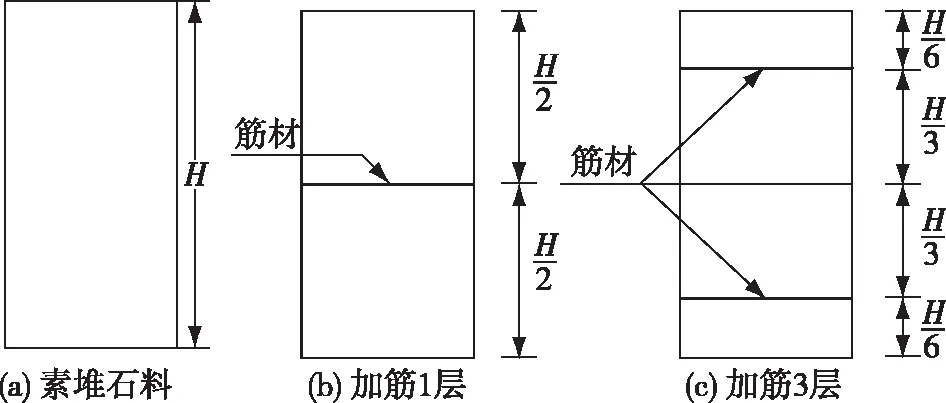
图1 加筋布置示意Fig.1 Sketchmap of reinforcement arrangement
1 试验方案
为了研究加筋堆石料复合体的动力残余变形特性,开展了加筋堆石料的动力大三轴试验,试验在南京水利科学研究院自行研制的1 500 kN大型动静三轴压缩试验仪上进行,加筋布置见图1,试验材料和试验方案见文献[10] 。
2 加筋前后堆石料残余变形的变化规律
在文献[9] 基础上,对试验结果进行进一步分析。图2为典型的未加筋、加筋1层和加筋3层堆石料残余应变与振次关系曲线(Kc=2.5,σ3=0.5mPa,σd=0.54σ3),由此可得出以下结论:
(1)加筋前后堆石料的动力残余变形发展规律大致相同,均表现为在循环荷载作用初期残余变形发展很快,且随着振次的增大,残余变形的发展有所减缓,并逐渐收敛趋于某定值。
(2)加筋能在一定程度上限制堆石料变形,加筋后堆石料残余变形明显降低,与未加筋堆石料相比,加筋1层堆石料残余轴向应变和体积应变的减小幅度分别为35%和25%,加筋3层堆石料残余轴向应变和体积应变的减小幅度分别为56%和41%,这表明随着加筋层数的增加,堆石料残余变形逐渐减小,但残余变形减小幅度将逐渐降低。
(3)在施加动荷载的初始时刻,加筋堆石料和不加筋堆石料的残余变形相差不大,加筋作用不明显,但随着振次增加,加筋作用开始体现,加筋堆石料和不加筋堆石料的残余变形相差越来越大,表明筋材对堆石料变形的限制作用必须在一定的扰动下才能发挥。
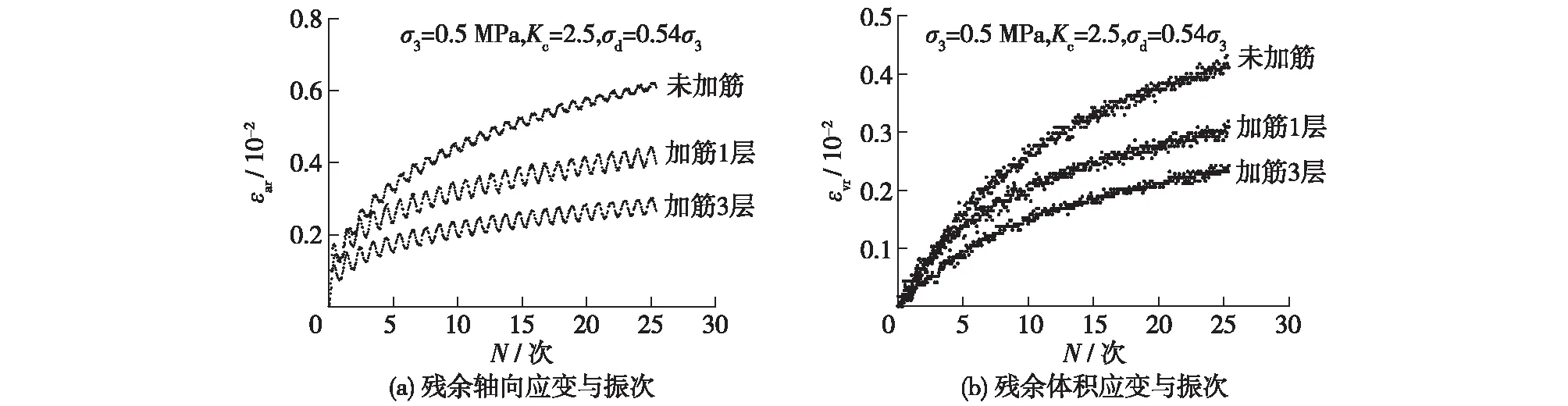
图2 堆石料残余应变与振次关系曲线Fig.2 Relationships between residual strain and vibration amplitude of rockfill
图3为两级动应力(σd=1.1σ3,σd=0.5σ3)下堆石料最大残余应变差值与围压的关系曲线,可知在相同围压下,残余应变差值从大到小为未加筋堆石料、加筋1层堆石料和加筋3层堆石料;在相同加筋条件下,最大残余应变的差值随围压的增加而增加。

图3 堆石料最大残余应变与围压的关系曲线Fig.3 Relationships betweenmaximum residual strain and confining pressure of rockfill
3 加筋堆石料的残余应变模型
沈珠江及其改进残余变形模型[11-12]在大坝动力残余变形的分析中应用广泛。该模型认为残余剪切应变γr和残余体积应变εvr的发展大体符合半对数衰减规律,即
εvr=cvrlg(1+N)
(1)
γr=cdrlg(1+N)
(2)
其中参数cvr和cdr的表达式为
(3)
cdr=c4γdc5Sl
(4)
式中:N为振次;γr=(1+μd)εar,其中εar为残余轴向应变;μd为动泊松比,可取0.33;c1和c2分别为cvr和γd双对数关系曲线γd=1%处的直线截距和拟合曲线的斜率;c4和c5分别为cdr/Sl和γd双对数关系曲线γd=1%处的直线截距和拟合曲线的斜率;Sl为应力水平。研究表明,应力水平对cvr影响很小,故可假定Sl对cvr无影响,即式(3)中的c3=0。
沈珠江残余变形模型能够较好地模拟试验获得的残余体积应变与振次的关系,但模拟残余剪切应变与振次的关系时,离散性较大,例如图4和5所示的残余剪切应变与振次的关系曲线。
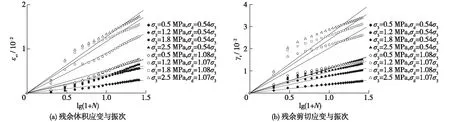
图4 残余应变与lg(1+ N)的关系曲线(加筋1层)Fig.4 Relationship curves between residual strain and lg(1+ N)(Reinforced with 1 layer)
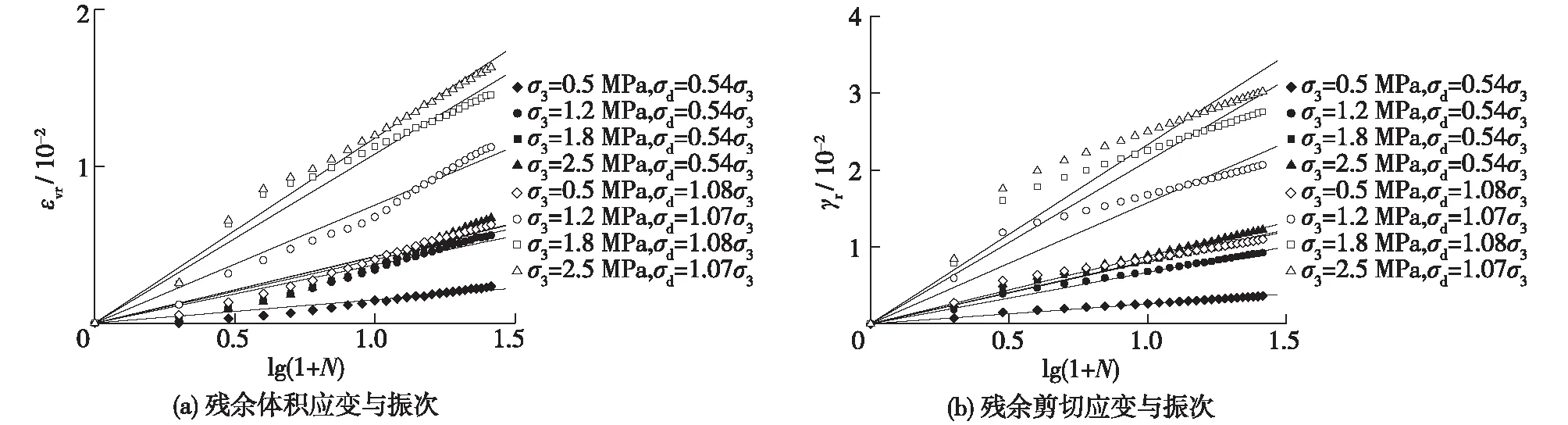
图5 残余应变与lg(1+N)的关系曲线(加筋3层)Fig.5 Relationship curves between residual strain and lg(1+N)(Reinforced with 3 layers)
针对半对数衰减规律模拟残余剪切应变与振次关系的不足,采用下式的指数关系替代式(2)的半对数关系,残余体积应变公式仍采用式(1)和式(3)。
γr=cdrNa
(5)
式中:参数a取常数;参数cdr仍采用式(4)。
利用式(5)拟合加筋前后堆石料残余剪切应变与振次的关系,发现当参数a取值在0.20~0.25范围内,拟合效果最好。图6和7分别为当模型参数a=0.20和0.25时,加筋1层和加筋3层堆石料残余剪切应变与振次a次方的关系曲线,可知当a=0.20时,拟合曲线与试验数据在高轴向动应力情况下的吻合度较好;当a=0.25时,拟合曲线在低轴向动应力情况下较好。
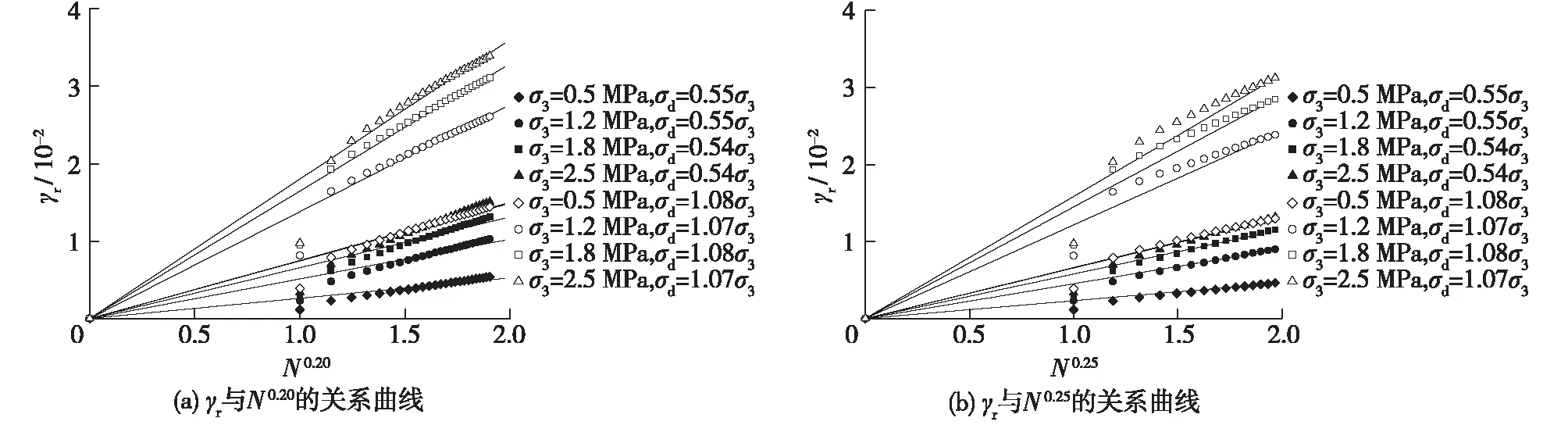
图6 加筋1层残余剪切应变γr与振次N 0.20和N 0.25的关系曲线Fig.6 Relationships between residual shear deformation γr and vibration grade N 0.20 and N0.25 of reinforced 1 layer
Tab.1 Dynamic residual deformation parameters of rockfill materials before and after reinforcement(c3=0)
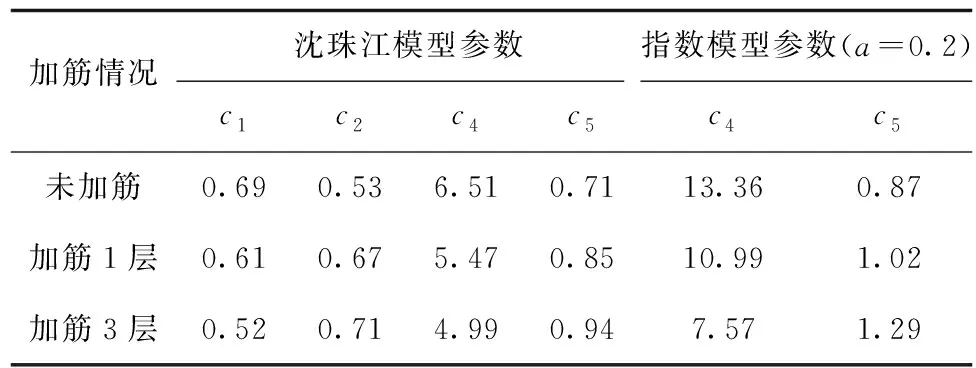
加筋情况沈珠江模型参数指数模型参数(a=0.2)c1c2c4c5c4c5未加筋0.690.536.510.7113.360.87加筋1层0.610.675.470.8510.991.02加筋3层0.520.714.990.947.571.29
以a=0.20时为例,拟合素堆石料、加筋1层堆石料和加筋3层堆石料的(cdr-Sl-υd)的关系曲线,最终获得加筋前后堆石料的动残余变形参数如表1所示。可知与未加筋相比,沈珠江模型和本文修改后的模型均表现为随着加筋层数的增加,参数c1和c4有所降低,而c2和c5略有增大。以上参数的变化表明了随加筋层数增加,堆石料抵御变形的能力逐渐增强。
4 筋材网孔大小的影响
为了研究筋材网孔大小对加筋堆石料动三轴试验结果的影响,在原试验方案[9]的基础上,重新设计了试验方案,开展了土工格栅加筋堆石料的动三轴试验。堆石料试样中的加筋层数为4层,等间距铺设,土工格栅裁剪后直径为280mm,网孔大小为正方形,网孔尺寸分别有边长为30和60mm两种。试验围压设置为1 500 kPa,固结应力比为2.0,轴向动应力为围压的80%,振次为25次。试验得到轴向应变和体积应变与振次的关系曲线如图8所示,可得出以下两点结论:
(1)土工格栅网孔直径为30mm试样的残余轴向应变略大于网孔直径为60mm的,推测格栅网孔大小越接近堆石料的最大粒径,堆石颗粒与格栅网孔之间的咬合作用发挥越好,试样的残余轴向应变就越小。
(2)土工格栅网孔直径为60mm试样的残余体积应变略大于网孔直径为30mm的,但两者的差值极小,推测网孔的变化对堆石料的残余体积应变影响较小,该差值可能是试验操作、试样制备等合理的误差引起的。
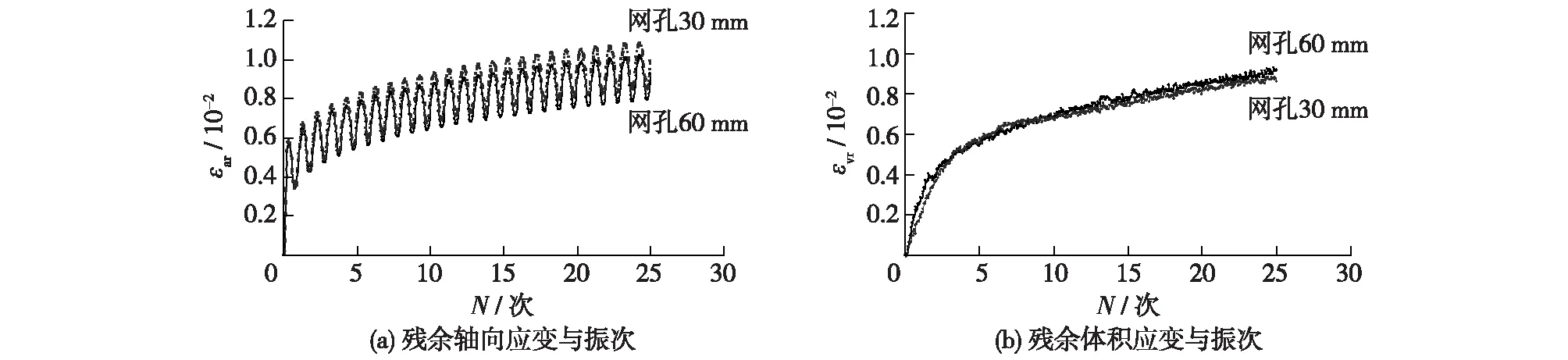
图8 残余应变与振次关系曲线Fig.8 Relationships between residual strain and vibration amplitude
5 结 语
基于加筋堆石料的动三轴试验结果,分析加筋前后堆石料的残余变形规律,得出:
(1)加筋前后堆石料的残余变形发展规律虽然大致相同,但加筋后堆石料残余应变数值明显降低。在循环荷载作用初期,残余变形均发展很快,随着振次的增大,残余变形的发展均有所减缓,并逐渐收敛趋于某定值,但加筋和不加筋堆石料残余变形的差值越来越大,表明筋材对堆石料变形的限制作用必须在一定的扰动下才能发挥。
(2)残余变形随围压和动应力比的增大而增大;高围压下加筋堆石料残余变形的减小幅度大于低围压下的;随着加筋层数的增加,残余变形减小幅度将逐渐降低。
(3)与沈珠江残余应变模型相比,构造的指数型经验式能较好地模拟加筋堆石料残余剪切应变与振次N的关系,拟合曲线与试验数据在高轴向动应力情况下的吻合较好。
(4)格栅网孔大小越接近堆石料的最大粒径,堆石颗粒与格栅网孔之间的咬合作用发挥越好,试样的残余轴向应变就越小,但格栅网孔大小对试样残余体积应变的影响较小。

