加翼桩水平承载力计算方法研究

陈灿明，何建新，苏晓栋，王曦鹏，黄卫兰

(1. 南京水利科学研究院水利部水科学与水工程重点实验室，江苏南京 210029； 2. 中国能源建设集团江苏省电力设计院有限公司，江苏南京 211102)

加翼桩作为新型海上风电基础，通过在泥面下的桩身设置翼板增加桩前土抗力，减小水平位移，以提高基础水平承载力[1]。由于目前有关加翼桩的研究甚少，更缺乏实测数据，为深入研究加翼桩的水平承载性能，通过海上风电大直径单桩与加翼桩水平承载性能数值模拟计算结果的对比分析，基于桩身土压力分布特点和受力机理，参考规范中的P-Y曲线模式对相关参数拟合修正，分析了加翼桩翼板参数对水平承载力的影响规律[2-4]，提出了适用于海上风电大直径加翼桩水平承载力经验式，为加翼桩研究和运用提供参考。

1 大直径单桩与加翼桩水平承载力对比

1.1 有关计算模型

以某5mW级海上风电机组为模型，钢管桩桩径5m，壁厚0.08m，桩长73m，入土深度55m。加翼桩采用一桩四翼对称布置，翼板与钢管桩双面焊接，壁厚0.08m，竖向为长度，水平向为宽度。按50年一遇荷载组合考虑风、浪、流等荷载，计算时将水平荷载简化为集中力、沿一组翼板中心线作用于泥面上18m的桩顶横截面中心。

采用三维实体有限元模型，水平向桩周土体取25倍桩径宽度，土层总厚度取1.3倍桩基入土深度。网格沿深度方向按0.1～1.0m间距划分，桩周环向按0.5m间距加密网格。钢管桩和翼板采用线弹性本构模型，地基土(C=25 kPa，φ=14°，ν=0.30，Es=7.5mPa)采用Mohr-Coulomb弹塑性本构模型，桩-土接触面采用主面-从面接触对算法计算，摩擦系数μ按罚刚度法计算[5-6]。

计算时当加翼桩最大应力达到材料允许强度250mPa或泥面处桩身倾斜率达到4‰时，认为加翼桩达到极限水平承载力状态[7-8]。

1.2 单桩和加翼桩水平承载性能对比

分别选取翼板面积、形状、埋深和刚度等4种翼板参数下加翼桩水平承载能力最优的工况，分别以FPA，FPJ，FPT，FPZ和FPEI表示，与同条件单桩(MP)从破坏形式、桩身弯矩、桩身位移、桩身应力和水平极限承载力等方面分析翼板对基桩水平承载力的影响。各工况翼板参数见表1。

表1 基桩模型翼板参数Tab.1 Wing plate parameters of pile foundation

1.2.1破坏形式 根据单桩与加翼桩水平极限荷载作用下位移云图(图1～2)，单桩与加翼桩在水平荷载作用下的破坏规律相似，加翼桩的破坏形式介于桩顶自由和桩顶受约束的单桩之间。桩前土体受挤压隆起变形直至开裂破坏，桩后土体发生桩土脱离形成空洞；两侧翼板出现较大扭曲变形。

加翼桩破坏既取决于桩周土体强度，也受桩身材料强度控制，随着翼板对基桩水平位移约束增强，桩身强度破坏逐渐由桩后侧受拉破坏转化为桩前上缘处受压破坏，桩前土体剪切破坏范围逐渐变大。

图1 极限荷载作用下单桩水平位移云图(单位：m)Fig.1 Horizontal displacement cloud diagram ofmonopile under ultimate load(unit:m)

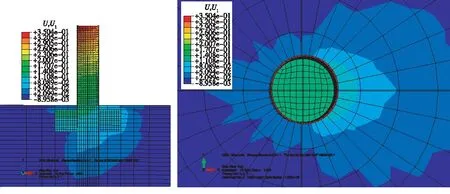
图2 极限荷载作用下加翼桩水平位移云图(单位：m)Fig.2 Horizontal displacement cloud diagram of wing-monopile under ultimate load(unit:m)

图3 水平荷载与桩身最大弯矩曲线Fig.3 Horizontal loads andmaximum bendingmoment curves of pile body

1.2.2桩身弯矩 加翼桩最大弯矩位置高于单桩，且随荷载增加越趋明显。水平荷载为1.5～12.0mN时，单桩桩身最大弯矩位于泥面下0.85D～1.68D，加翼桩桩身最大弯矩位于泥面下0.63D～1.59D。

水平荷载与桩身最大弯矩曲线见图3，加翼桩较单桩桩身最大弯矩值的降幅随荷载增大而增大，增速逐级趋缓。最大翼板面积加翼桩FPA(面积2.56D2)和最优梯形翼板加翼桩FPT(面积D2)较单桩桩身最大弯矩降低效果最显著，12.0mN荷载作用时两种加翼桩桩身最大弯矩较单桩分别降低9.7%和10.2%，说明翼板面积和翼板形状是提升加翼桩水平承载力的主要因素。

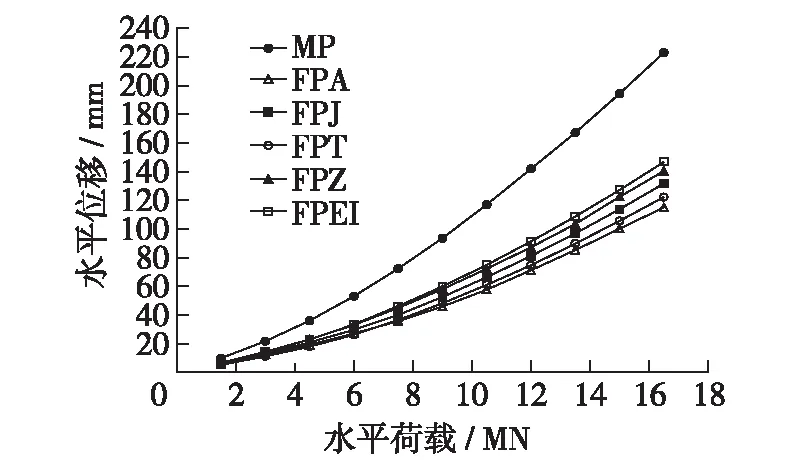
图4 水平荷载与泥面处水平位移曲线Fig.4 Horizontal loads and horizontal displacement curves atmud surface of pile

1.2.3桩身位移 水平荷载与基桩泥面处水平位移曲线见图4。计算结果表明：水平荷载作用下加翼桩水平位移明显小于单桩，加翼桩较单桩水平位移的降低幅度随水平荷载增大先显著增大后逐渐趋于稳定。

最大翼板面积加翼桩FPA和最优梯形翼板加翼桩FPT对于桩身泥面处水平位移降低效果最显著，12.0mN荷载作用下两种加翼桩泥面处水平位移与单桩比分别降低49.8%和47.4%，说明翼板面积和翼板形状是影响加翼桩水平位移的最敏感因素。

加翼桩翼板可有效降低基桩的水平位移，其对水平位移的影响大于对桩身弯矩的影响。

1.2.4桩身应力 在9.0mN水平荷载作用下单桩与加翼桩的桩身应力云图见图5。计算结果显示，加翼桩翼板周围桩身区域形成应力集中，应力集中程度最高在桩前侧上翼缘附近的最大压应力区和桩后侧上翼缘附近最大拉应力区。翼板以下深度范围加翼桩桩身应力小于单桩，并随深度增加逐渐趋于一致。

加翼桩桩身最大应力位置高于单桩，同级荷载条件下的最大应力值相差较小。

图5 水平荷载作用下桩身应力云图(H=9.0mN )(单位：Pa)Fig.5 Stress cloud chart of wing-monopile body under horizontal loads (H=9.0mN )(unit: Pa)

Tab.2 Horizontal ultimate bearing capacity and stresses ofmonopile and wing-monopile

基桩编号极限水平承载力/MN加翼桩/单桩/%泥面处倾斜率/‰桩身最大应力/MPaMPFPAFPJFPTFPZFPEI8.8814.9713.8314.6013.1212.65100168.58155.74164.41147.75142.454.004.004.004.004.004.00150.64144.05221.77248.04213.42199.70

1.2.5基桩极限水平承载力 单桩与加翼桩水平极限承载力及相应应力计算结果见表2。

单桩水平极限承载力一般由桩身泥面处的倾斜率控制，加翼桩水平极限承载力则根据翼板参数不同由桩身泥面处的倾斜率或桩身材料强度控制。当加翼桩翼板参数合理时，极限荷载时桩身泥面处的倾斜率达到4‰，桩身应力基本接近材料强度。

相同荷载作用时加翼桩桩身最大应力和桩基倾斜率小于单桩，说明翼板可有效减小桩身位移和桩身最大应力。

加翼桩水平极限承载力远大于单桩，最大翼板面积加翼桩FPA和最优梯形翼板加翼桩FPT比单桩MP水平极限承载力增幅最大，达68.6%和64.41%。由于梯形翼板面积仅为最大翼板面积的39.06%，因此倒梯形翼板对提升桩基承载力效果最好，翼板利用率最高。

2 单桩与加翼桩桩身土压力分布对比分析

图6 水平极限承载力时单桩和加翼桩接触压应力云图(单位：Pa)Fig.6 Contact compress stress cloud chart ofmonopile under horizontal ultimate bearing capacity(unit: Pa)

桩侧土压力源于水平荷载作用下桩身水平位移[9-10]，选择长宽比0.39的矩形翼板加翼桩FPJ1为研究对象，与单桩MP进行桩身土压力分布对比分析，文中所述土压力均为节点CPRESS值，图6为水平极限荷载作用时单桩和加翼桩的接触压应力云图，图7和8为极限荷载作用下单桩和加翼桩泥面下1.5m深度处土压力系数分布。

单桩和加翼桩的土压力均沿荷载作用方向对称分布，桩前土压力较大且变幅较小，桩后侧土压力为零，说明桩土已发生分离。单桩最大土压力为203.94 kPa，位于桩前端；加翼桩桩身最大土压力为230.53 kPa，位于桩身两侧45°位置，翼板部分最大土压力为209.83 kPa，位于翼板与桩身连接处。翼板上土压力从近桩身端向远桩身逐渐减小。加翼桩翼板范围内土压力随深度增加而先增大达到最大值后逐渐减小，翼板下桩身土压力随深度的变化规律与单桩相同，但变幅小于单桩，说明加翼桩有效限制了桩身位移和转动。

图7 单桩土压力系数分布Fig.7 Distribution of earth pressure coefficients onmonopile

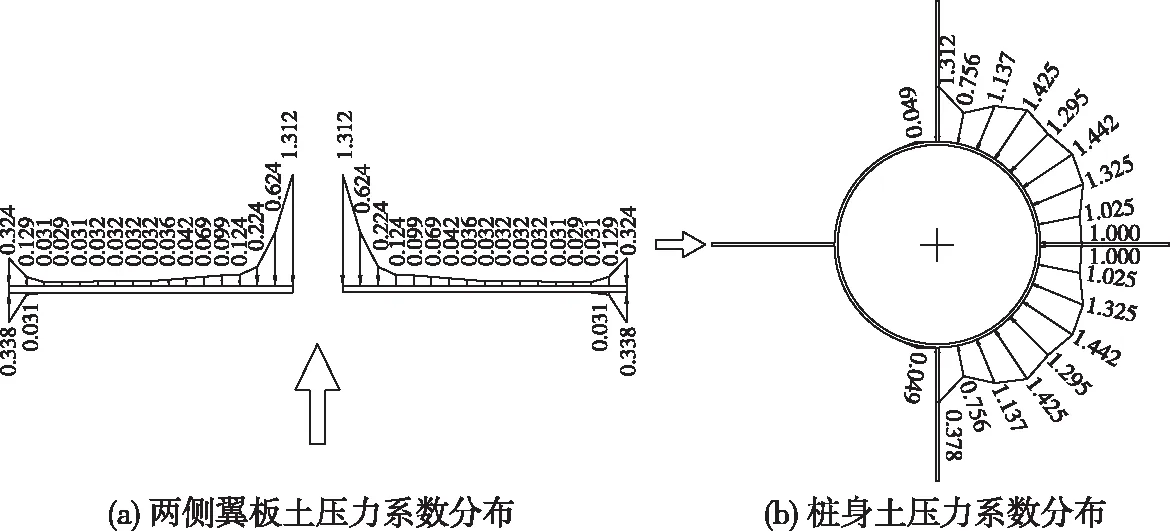
图8 加翼桩土压力系数分布Fig.8 Distribution of earth pressure coefficients on wing-monopile

3 海上风电基础大直径单桩P-Y曲线经验式

P-Y曲线法计算桩基水平承载力是现行规范推荐的方法之一[11-13]，主要适用于小直径桩基，它能对桩、土体作非线性分析，横向荷载作用下土的反应可由土体沿深度的应力-位移曲线(P-Y曲线)来表达，各深度处的P-Y曲线互不干扰，并共同构成一个曲线簇来表达桩土体系的应力应变性状。为推求大直径单桩极限水平承载力Hu.MP，参考现行规范中P-Y曲线模式，根据单桩数值模拟结果对相关系数进行修正。

提取单桩泥面及以下0.5, 1.0, 1.5, 2.0和2.5m深度，在1.5, 3.0, 4.5, 6.0, 7.5和9.0mN水平荷载作用下的桩身位移和土抗力，绘制土抗力与桩身位移曲线见图9，修正后适用大直径桩的P-Y曲线见图10。

图10 修正后适用于大直径桩的P-Y曲线Fig.10 Modified P-Y curve for large diameter pile

修正后桩侧单位面积极限土抗力标准值Pu可按式(1)计算，并取较小值；修正后的P-Y曲线关系式见式(2)～(4)。

(1)

(1)当y/y50<3.58时，

(2)

y50=ρε50d

(3)

(2)当y/y50≥3.58时，

P=Pu

(4)

式中：Cu为原状黏性土不排水抗剪强度标准值(Cu≤96 kPa)；γ为土重度(kN/m3)；d为桩径(m)；ξ为系数，取4.5～5.5；z为泥面以下深度(m)；Zr为极限水平土抗力转折点的深度(m)；P为泥面以下z深度处作用于桩上的水平土抗力标准值(kPa)；y50为桩周土达到极限水平土抗力之半时相应桩的侧向水平变形(mm)；ρ为相关系数，取8.0；ε50为三轴仪试验中最大主应力差一半时的应变值，取0.010。

图11 水平荷载与泥面处水平位移Fig.11 Horizontal load and displacement of pile atmud surface

ABAQUS数值模型、规范P-Y曲线和修正的P-Y曲线3种算法计算大直径桩基泥面处水平位移与荷载关系曲线见图11。计算结果显示，修正的P-Y曲线法与实体模型计算结果吻合较好，说明基于地勘资料或现场原位试验数据修正的P-Y曲线法能较准确推求大直径单桩水平承载力，规范P-Y曲线法用于大直径单桩水平承载力计算时存在较大误差。

4 加翼桩水平承载力计算经验式

由于水平荷载作用下大直径单桩和加翼桩的受力机理基本相同，最大区别在于加翼桩由于翼板的存在，增加了土抗力，限制了桩身泥面处的位移和倾斜率，从而提高总体承载力。以相同基桩条件的单桩水平极限承载力为基础，考虑加翼桩翼板面积、形状、埋深和刚度等因素的影响，推导加翼桩水平极限承载力的经验式。

根据加翼桩翼板参数对承载力影响的研究结果，提出基于大直径单桩水平极限承载力、考虑翼板参数影响的软黏土地基大直径加翼桩极限承载力经验式和翼板参数影响系数：

Hu.FP=αk1k2k3k4Hu.MP

(5)

k1=0.005 2(S/D2)3-0.099 2(S/D2)2+0.452 9(S/D2)+1.077，S/D2∈[0.09,3.24]

(6)

k2.J=-0.068ln(L/W)+1.024 2，L/W∈[0.39,2.56]

(7)

k2.T=8.418 7(θ/π)3-10.411(θ/π)2+3.480 4(θ/π)+0.797 4，θ/π∈[0.15,0.62]

(8)

k3=-0.011(EI/(E0I0))2+0.038 7(EI/(E0I0))+0.974，EI/(E0I0)∈[0.6,4.0]

(9)

k4=-1.731 7(Z/D)4+4.141 1(Z/D)3-3.184 2(Z/D)2+0.709 4(Z/D)+1，Z/D∈[0,0.8]

(10)

式中：Hu.FP为加翼桩极限承载力；Hu.MP为单桩极限承载力；α为综合影响系数；k1为翼板面积影响系数；k2为翼板形状影响系数，考虑矩形和梯形两种形状，分别为k2.J和k2.T；k3为翼板刚度影响系数；k4为翼板埋深影响系数。

翼板面积影响系数中，S/D2为翼板面积与桩径平方比，拟合曲线与实体模型计算点相关度为0.970。

矩形翼板形状影响系数中L/W为翼板长宽比，拟合曲线与实体模型计算点相关度为0.917。梯形翼板形状影响系数中θ为梯形斜边与上缘内夹角(单位rad)，拟合曲线与实体模型计算点相关度为0.973。

翼板刚度影响系数中，EI/(E0I0)为翼板刚度与钢管桩等厚翼板的刚度比，拟合曲线与实体模型计算点相关度为0.997，根据拟合曲线计算，翼板刚度比EI/(E0I0)为1.768时，加翼桩水平极限承载力最大。

翼板埋深影响系数中，Z/D表示翼板埋深与桩径比，拟合曲线与实体模型计算点相关度为0.998，根据拟合曲线计算，翼板埋深Z/D为0.153时，加翼桩水平极限承载力最大。

5 结 语

基于ABAQUS三维数值仿真模型，针对海上风电大直径单桩与加翼桩水平承载性能开展研究，得出如下结论：

(1)加翼桩与单桩在相同水平荷载作用下，最大弯矩可降低10%左右，泥面处最大水平位移可降低40%左右。极限承载力可提高60%左右。

(2)大直径单桩水平极限承载力一般由桩身泥面处的倾斜率控制，加翼桩水平极限承载力则根据翼板参数不同由桩身泥面处的倾斜率或桩身材料强度控制。当加翼桩翼板参数合理时，极限荷载时桩身泥面处的倾斜率达到4‰，桩身应力基本接近材料强度。

(3)水平极限承载力状态时，加翼桩桩前土体受挤压隆起变形，桩后土体出现桩土脱离形成空洞；土压力沿荷载作用方向对称分布，桩前土压力较大，桩后侧土压力为零。桩身最大土压力位于桩身两侧45°位置，翼板土压力从近桩身端向远桩身逐渐减小，最大土压力位于翼板与桩身连接处。

(4)基于地勘资料或现场原位试验、参考规范P-Y曲线模式，对相对系数进行修正的P-Y曲线法能较准确推求大直径单桩水平承载力。规范P-Y曲线法计算大直径单桩水平承载力时误差相对较大。

(5)以相同条件单桩水平极限承载力为基础，根据研究成果提出考虑加翼桩翼板面积、形状、埋深和刚度等因素的加翼桩水平极限承载力的经验公式和翼板参数影响系数计算式，影响系数拟合曲线与实体模型计算点相关度为0.917～0.997。