某框架结构减、隔震方案对比
李晓玮 施卫星 王建峰 虞终军
(1.同济大学结构工程与防灾研究所,上海 200092; 2.同济大学建筑设计研究院(集团)有限公司,上海 200092)
0 引 言
建于地震高烈度区或者安全等级较高的框架结构,传统的抗震设计主要靠增大构件截面尺寸或增加斜撑等加强结构刚度的方法实现。但这些方法同时也增大了结构的地震作用,造成经济上的浪费,甚至威胁结构的安全性。自从J.T.P.Yao (姚治平)1972年将现代控制理论引入土木工程[1]开始,减隔震方法逐渐被工程师所理解和接受,其优越的抗震性能已经在很多工程实例中得到证实。
基础隔震技术的原理是延长结构的自振周期,让大位移主要发生在结构底部与基础之间的隔震层,并提供适当的阻尼减小隔震层的响应,通过减小地震输入保证上部结构的位移满足使用要求[2]。消能减震技术是把结构的某些部分,如支撑、剪力墙、节点等设计成耗能构件。这些耗能构件可以分为两大类,分别是位移相关型和速度相关型阻尼器[3]。由于位移型阻尼器成本低、制造安装相对简单,所以应用更为广泛。其原理是在结构出现大变形时,耗能构件进入非弹性状态,产生较大塑性变形消耗地震能量,保护结构免遭破坏。
本文针对某三层学校建筑,分别进行了传统抗震设计、隔震和使用软钢阻尼器的减振设计,对比了它们的减震效果和经济性,得出结论以便于工程应用。
1 工程概况及传统设计
该三层框架混凝土学校建筑,建造于8度区,基本地震加速度为0.20g,设计地震分组为第三组。场地类别为II类,特征周期0.45 s。由于该建筑属学校用房,抗震设防类别为乙类。安全等级一级,重要性系数1.1。该结构采用柱下独立基础,首层地面采用压实的天然地坪。
按照传统方法进行设计,柱子采用600 mm×600 mm截面,外边框主梁采用300 mm×700 mm,内框主梁采用300 mm×600 mm,次梁采用250 mm×500 mm截面。此时,该结构前三阶周期分别为0.584 3 s,0.574 0 s,0.497 9 s;地震作用下最大层间位移角X方向为1/565,Y方向为1/606;底层框架柱最大轴压比为0.33;基底剪力X方向3 775 kN,Y方向3 741 kN;且所有梁柱配筋验算满足要求。该方案的混凝土和钢筋用量见表1。
表1各方案材料用量表
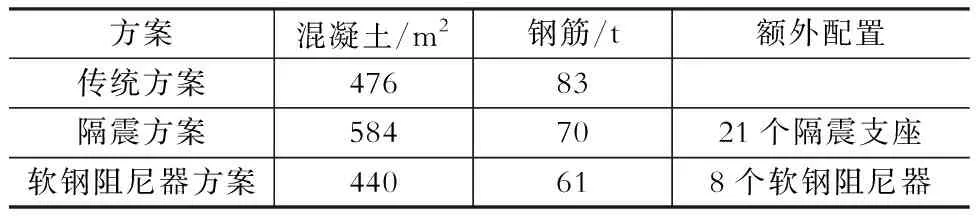
Table 1Material scale of each program
注:①上表为主体结构工程量估值,不包括填充墙等二次结构,混凝土和钢筋用量均不包括基础部分;
②该表不能反映由于设置隔震层后引起的隔震支墩、建筑设缝、设备管线、沟槽等处理所增加的造价。软钢阻尼器方案不包括连接阻尼器预留预埋等造价。
该建筑计算地震反应谱时主要采用盈建科(YJK-1.7.1.0)和ETABS 2015软件,分析时采用CQC振型效应组合方式,考虑扭转耦联效应,同时考虑偶然偏心的影响。多遇地震、设防地震以及罕遇地震下的弹性和弹塑性时程分析主要采用ETABS2015。通过对比两种软件所建模型的质量、周期和地震层剪力等指标,验证了两种模型的准确性和有效性。
2 隔震方案设计
隔震设计的总体步骤为,初步拟定隔震目标,即确定水平向减震系数(实际操作时一般根据设计习惯确定抗震设防烈度降低半度还是一度)[4];按照降低的抗震烈度进行结构设计,在±0.000处增加一层梁板,柱向下延伸800 mm。为接近真实受力,柱底采用铰接[5]。采用时程法计算设防地震下隔震结构的水平向减震系数,并调整支座参数使其与减震目标相匹配;进行罕遇地震作用分析,进行支座设计。

图1 结构轴测图Fig.1 Isometric view of structure
2.1 初步拟定减震目标及构件设计
采用隔震支座后,预计结构减小的地震输入相当于地震设防烈度降低一度,即多遇地震下水平地震影响系数最大值取0.08。隔震层、一层、二层的柱截面采用550 mm×550 mm,顶层柱子采用500 mm×500 mm截面,底层柱底设铰;外边框主梁和纵向框架梁采用300 mm×600 mm,内框横向主梁采用250 mm×500 mm,次梁采用200 mm×500 mm截面。此时,该结构前三阶周期分别为0.772 3 s,0.735 4 s,0.648 8 s;地震作用下最大层间位移角X方向为1/662,Y方向为1/587;底层框架柱最大轴压比为0.48;基底剪力X方向2 057 kN,Y方向1 937 kN;同样地,所有梁柱配筋验算满足要求。该方案的混凝土和钢筋用量见表1。
2.2 中震计算
根据《建筑抗震设计规范》(GB50011—2010,以下简称《抗规》)12.2.5条,隔震后的水平地震影响系数αmax1=βαmax/ψ(αmax1为隔震后的水平地震影响系数最大值;β为水平向减震系数;αmax为非隔震的水平地震影响系数最大值;ψ支座种类的调整系数),其中水平向减震系数为按弹性计算所得的隔震与非隔震各层层间剪力的最大比值,对于高层建筑,尚应考虑倾覆力矩的比值,当采用时程分析时,取设计基本地震加速度(中震)输入计算。
根据《抗规》12.2.3条,同一隔震层内各个橡胶隔震支座的竖向压应力宜均匀,竖向平均应力不应超过限值12 MPa。本工程共使用了21个支座,各类型支座的数量及力学性能详见表2,隔震支座平面布置见图2。
表2铅芯橡胶支座力学参数

Table 2Parameters of LRB
该方案采用ETABS2015中的Rubber Isolator连接单元来模拟铅锌橡胶支座,U1方向设定其弹性刚度为支座的竖向抗压刚度。U2、U3代表支座的水平方向,分别采用双线性的刚度模型模拟铅锌橡胶支座的水平向的刚度和阻尼特性。
根据《抗规》5.1.2条规定,本工程选取了2条强震记录和1条人工模拟加速度时程,满足地震响应系数曲线在统计意义上的相符和结构底部剪力的要求。《叠层橡胶支座隔震技术规程》(CECS 126:2001)规定,隔震房屋两个方向的基本周期相差不宜超过较小值的30%。隔震后两个方向的周期分别为2.171 7 s和2.164 2 s,满足差值要求。
表3、表4为隔震、非隔震结构各层剪力对比情况,结构各层(不考虑隔震层)层间剪力的最大比值为0.42。根据《抗规》12.2.5条,隔震后水平地震影响系数αmax1=βαmax/ψ=0.42×0.16/0.8=0.084。与多遇地震设计时的减震目标基本相当。根据《抗规》12.2.5条,本项目的水平向减震系数大于0.3,隔震层以上结构可不进行竖向地震作用的计算。

图2 铅芯橡胶支座布置图Fig.2 Layout of LRB
表3X向非隔震与隔震结构各层层间剪力及比值

Table 3The inter-story shear and it’s ratio of isolated and non-isolated structure on X-direction
注:隔震层的剪力对比值不计入减震系数
2.3 大震计算
在罕遇地震作用下,隔震支座不宜出现拉应力,当少数隔震支座出现拉应力时,其拉应力不应大于1 MPa。根据《抗规》12.2.9条规定:隔震层的支墩、支柱及相连构件,满足罕遇地震下隔震支座底部的竖向力、水平力和力矩的承载力的要求;隔震层以下的地下室满足嵌固刚度比和隔震后设防地震的抗震承载力要求,并满足罕遇地震下的抗剪承载力要求。罕遇地震下需验算隔震支座处的轴力、剪力用于支墩设计,并验算隔震层水平位移,使其满足规范要求的不应超过支座有效直径的0.55倍和支座内部橡胶总厚度3.0倍二者的较小值。
表4Y向非隔震与隔震结构各层层间剪力及比值

Table 4The inter-story shear and it’s ratio of isolated and non-isolated structure on Y-direction
注:隔震层的剪力对比值不计入减震系数。
隔震支座拉应力验算应采用的荷载组合:1.0×恒荷载-0.5×竖向地震±1.0×水平地震。由表11可知,在罕遇地震作用下,只有极少数支座处出现拉应力,且支座处的最大拉力出现在14号支座处,最大拉应力为0.98 MPa,小于1.0 MPa,隔震支座满足规范要求。
罕遇地震下隔震层水平位移计算采用的荷载组合:1.0×恒荷载+0.5×活荷载+1.0×水平地震,得到罕遇地震下各个支座最大水平位移。本工程中隔震支座的水平位移最大值为250.4 mm,不超过其有效直径的0.55倍(以LRB500支座为例:0.55×有效直径=275.0 mm)和各橡胶层总厚度3倍(以LRB500支座为例:3×橡胶层总厚度=288.0 mm)的较小值,满足设计要求。
根据《抗规》12.2.9条规定:与隔震层连接的下部构件的地震作用抗震验算,应采用罕遇地震下隔震支座的竖向力、水平力和力矩进行计算。图4中,P为在罕遇地震时设计组合工况下产生的轴向力;Vx和Vy为罕遇地震时设计组合工况下产生的X和Y向水平剪力。Ux、Uy为罕遇地震作用下隔震支座产生的水平位移;Hb为隔震支座高度,H为隔震支墩的高度。则有,隔震支座下支墩顶部产生的弯矩;Mx=P×Ux+Vx×Hb,My=P×Uy+Vy×Hb,用于支座连接件的承载力设计;隔震支座下支墩底部产生的弯矩:Mx=P×Ux+Vx×(Hb+H)My=P×Uy+Vy×(Hb+H),结合前面直接求得的轴力N,剪力Vx、剪力Vy,可以进行支墩的设计。
3 软钢阻尼器方案
考虑在结构上布置8组软钢阻尼器(一层、二层每个方向布置两组,共计8组),阻尼器力学参数为:弹性刚度K=2.0× 105kN/m,屈服力=200 kN,第二刚度比0.02,其他产品参数见表5。阻尼器均采用墙支撑方式与主体结构相接合,可以利用建筑隔墙位置布置,适宜于建筑上的造型,不影响门框洞口,如图5所示。阻尼器的平面布置如图7所示。主体结构一层、二层、三层柱子均采用550×550截面,阻尼器邻近柱子和边跨框架柱采用600×600截面;主梁采用300×600截面,阻尼器邻近框架梁采用300×700截面,次梁采用200×500截面。此时,该结构前三阶周期分别为0.700 9 s,0.651 0 s,0.620 9 s;地震作用下最大层间位移角X方向为1/608,Y方向为1/574;底层框架柱最大轴压比为0.37;基底剪力X方向3 535 kN,Y方向3 534 kN;同样,所有梁柱配筋验算满足要求。该方案的混凝土和钢筋用量见表1。
表5软钢阻尼器产品参数

Table 5Parameters of mild steel damper
软钢阻尼器与防屈曲支撑(BRB)的区别在于:BRB经常作为斜撑的形式布置在结构中,小震作用下处于弹性状态,相当于普通钢支撑,为结构提供侧向刚度,而在中震和大震下通过钢芯材的屈服来耗能。BRB作为主体结构的一部分,其体量通常较大,难以更换。但是软钢阻尼器由于其体型小巧、布置灵活而便于更换的特性,使得软钢阻尼器有条件设计成小震作用便屈服的形式,即小震作用下钢阻尼器就能依靠自身的屈服耗散更多能量,进而提高结构的阻尼比。小震屈服的软钢阻尼器设计,使得该方案有了和隔震设计相似的经济性。如图8所示,在小震作用下结构梁柱均处于弹性状态,只有软钢阻尼器进入屈服,可见阻尼器参数的设置达到了预期的小震耗能效果。
图3 ETABS2015铅芯橡胶支座参数设置Fig.3 Parameters of LRB in ETABS 2015

图4 隔震支座支墩受力图Fig.4 Force diagram of isolation support pier
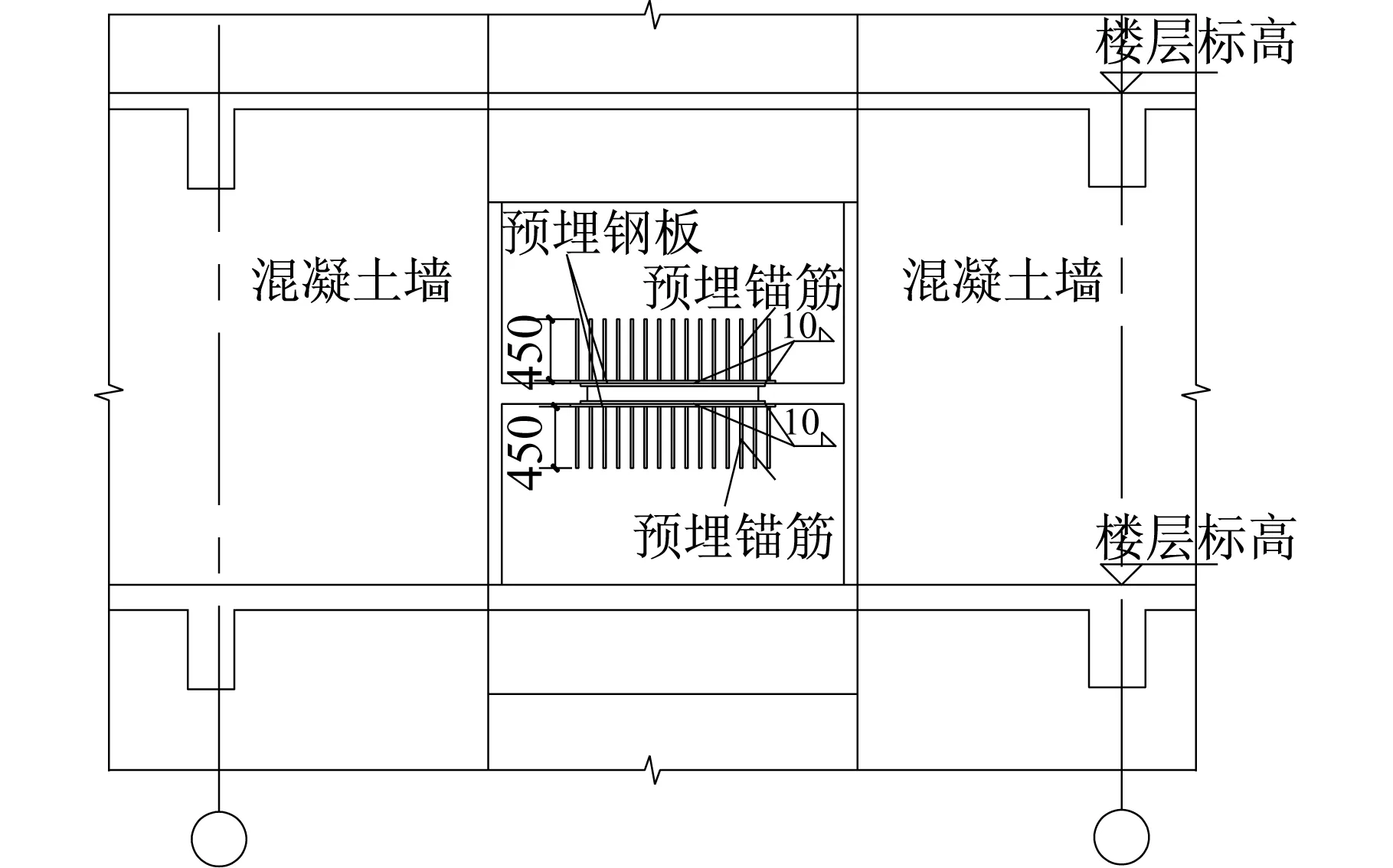
图5 采用墙支撑连接方式的示意图Fig.5 Schematic of connections of wall support
采用ETABS2015中的Plastic (Wen)连接单元来模拟软钢阻尼器,U1方向设定其弹性刚度为阻尼器的竖向抗压刚度。U2或者U3代表支座的作用方向,同样采用双线性的刚度模型模拟软钢阻尼器在该方向的刚度和阻尼特性。
图6 ETABS2015软钢阻尼器的参数设置Fig.6 Parameters of mild steel damper in ETABS 2015
对于小震屈服的软钢阻尼器,采用多遇地震下的弹塑性时程分析可以直接得到较为精确的构件和结构耗能状态,进而推算小震下的等效附加阻尼比。时程分析时,阻尼器由真实尺寸的墙体和连接单元组合模拟,连接单元采用具有两折线的滞回模型。结构的附加阻尼比按照《抗规》12.3.4条计算,等效刚度由阻尼器的最大阻尼力和位移的比值得到。另一种获得等效阻尼比的方法是利用等值线性法[6]将前一次修正了的阻尼器等效刚度和结构附加阻尼比代入反应谱法计算,经4~5次迭代后可以得到收敛结果。通过对比可知等值线性法得到的附加阻尼比略大于弹塑性时程法,其差值在15%以内,所以两种方法均可采用。本方案计算所得附加阻尼比为2.5%,取两种方法计算的较小值。
对结构进行罕遇地震下的弹塑性分析,一方面确保结构位移满足规范要求,观察其破坏形式,针对薄弱部位进行加强;另一方面,确定阻尼器在罕遇地震作用下的极限阻尼力[7],并根据大震下内力对阻尼器邻近的梁柱以及阻尼器的连接墙体进行配筋计算,确保连接阻尼器的主体结构在大震下有效发挥作用(依据《建筑消能减震技术规程》(JGJ 297—2013))。
经计算,在罕遇地震作用下,结构最大层间位移角小于规范限值1/50,符合《抗规》5.5.5条的规定。建筑物可实现“大震不倒”的抗震设防目标;由图9所示,塑性铰最先出现在软钢阻尼器处,随后主要出现在框架梁上,柱塑性铰出现较少。可见,整体结构布置合理,能够满足大震下抗震设防的要求。

图7 一层和二层软钢阻尼器平面布置图Fig.7 Layout of mild steel dampers on the first floor and second floor

图8 小震下结构塑性铰Fig.8 Plastic hinges under minor earthquake

图9 大震下结构塑性铰Fig.9 Plastic hinge under rare earthquake
4 传统设计、减隔震方案对比
4.1 工程造价对比
由表1可知,本项目主体结构造价,传统方案造价最高,其次隔震方案高于减震方案。由于隔震结构在建筑、结构、设备构造上较为复杂,以及后期维护需要另外的费用,故隔震方案的实际造价将高于估算。
4.2 减震效果和构造措施对比
从隔震技术应用于建筑工程的实际效果来看,应用隔震技术后,地震作用可降低1度甚至1.5度。然而需要设置隔震支座、隔震层及相对应构造措施,因此:
(1) 一般来说对于设防烈度为8度以上的较高楼层的建筑,可以节约投资成本;对于较低楼层的建筑由于增加的隔震层在整栋建筑的主体结构造价中所占比例较高,故虽然隔震层以上结构梁柱造价有所降低,但整体的主体结构造价反而较高。
(2) 隔震层以上的上部结构与周边任何固定物均应有隔离空隙。竖向隔离空隙为20 mm,水平隔离空隙为1.2倍罕遇地震时隔震支座最大水平位移。当平面不规则的建筑物需要设置抗震缝,抗震缝两侧建筑均需要隔震,水平缝宽将是上述要求的两倍,缝宽甚至可以达到1 m左右。建筑设计上,对建筑的外观、功能的布置造成影响,且较宽抗震缝的处理也较为困难。
(3) 隔震支座需要进行定期检查和维护,其后期维护成本较高。
软钢剪切阻尼器,利用软钢的屈服耗能为主体结构提供附加阻尼,可以减轻主体结构的地震反应。其特性表现在:
(1) 框架中运用软钢阻尼器,既可以提供结构抵抗地震作用、减小层间位移所需的抗侧刚度,又可以靠其小震屈服形成滞回环增加结构的阻尼比,所以上部结构梁柱可以减小尺寸,使结构自重有较大程度降低。
(2) 相比于隔震支座结构,基础设计构造与一般普通结构相同不需考虑隔震层,施工简单、快捷,不需另外后期维护,不增加基础造价。
(3) 软钢阻尼器上下通过两片墙体连接,利用建筑隔墙位置布置,适宜于建筑上的造型,不影响门框洞口的布置。地震过后软钢阻尼器检查、修复方便,便于建筑在地震过后的迅速修复使用。
5 结 论
综上所述,对于多层建筑,采用隔震支座和软钢阻尼器均能起到降低地震作用,改善结构抗震性能的作用。由于使用了隔震支座或者软钢阻尼器,结构构件(比如梁、柱)尺寸可以大幅度减小,有利于建筑的使用功能需要。
经过对比验证,本文提到的阻尼比的两种计算方法,即非线性时程法和线性迭代法,对于多层框架结构均为有效。非线性时程法经过一次计算可得到结构构件和阻尼器耗能数据,而线性迭代法也只需要经过4~5次迭代计算,所以两种计算方法的时间成本相差不大。
隔震支座设计时为满足较小的减震率需要尽量使用具有较小刚度的支座,而过小的刚度会使大震下支座的位移超出限值,实际工程中可以采用橡胶支座、铅锌橡胶支座和滑板支座(释放水平刚度)的组合形式来达到隔震层刚度小而阻尼大的特性。
从经济性的角度来看,隔震支座由于需要在隔震层上增加一层结构层,而且为了实现隔震层的滑移,水、电管线需要专门排布,这些都会给设计、施工和使用造成困难。而软钢阻尼器由于其布置灵活、可更换的特点更适合于多层建筑的抗震设计。

