扭转方向非理想振型的广义气动力谱修正

李阳阳 冯松宝 陈园园 孙 磊

(宿州学院资源与土木工程学院,宿州 234000)

0 引 言

在扭转方向,传统计算结构等效静力风荷载的方法如阵风荷载因子法以及高频底座天平技术,为了计算方便均假设第一阶振型为理想的振型[1-2]:第一阶振型为一个常数,振型在高度方向不发生变化。然而,近年来随着社会经济的发展和城市化进程的加快,建筑高度被不断突破,部分高层建筑的质量和刚度也出现了沿高度的不均匀分布,此类建筑的第一振型已不满足原有的理想振型而呈现出非理想振型,振型沿高度方向已不再简单的是一个常数。假设结构第一阶振型为理想振型而推导出的阵风荷载因子法以及高频底座天平技术,在出现非理振型的情况时,难免就出现了误差。

在扭转方向,许多国内外学者研究了非理想振型对高层建筑广义气动力谱的影响。Tschanz指出当结构的第一阶振型为非理想振型时,建议对高频底座天平测出的基底扭矩进行修正,并根据天平测得的基底剪力提出了一个近似的修正因子[3]。Kareem以某一高层建筑为研究对象,发现高频底座天平技术与测压试验技术得出的基底扭矩存在着很大的差异,并建议修正天平试验测出的基底扭矩[4]。Vickery指出非理想振型对于广义脉动风荷载的影响,是不同于基底弯矩和加速度的,但是没有给出具体的修正方法[5]。根据脉动风荷载沿高度完全相关和完全不相关的性质,Holmes得到了广义脉动风荷载关于振型指数β的修正公式[6]。Tallin基于多点瞬态同步测压试验的数据,建议对广义扭矩采用0.7的保守修正因子[7]。日本建筑学会对高频底座天平技术测出的结构顶部位移建议按如下公式修正:0.73+0.27β,β是第一阶振型的指数[8]。

在扭转方向,本文结合脉动风荷载的相干函数,依据数值积分的方法计算得出非理想振型的广义气动力谱与理想振型的广义气动力谱比值,并给出关于振型指数β的修正公式,以提高阵风荷载因子法以及高频底座天平技术等传统计算结构风致响应的可靠性。

1 广义气动力谱修正公式

1.1 基本公式推导

扭转方向的风荷载是由来流紊流和尾流激励共同作用产生的,与横风向风荷载的机理类似,它是由迎风面、侧风面和背风面的不对称风压分布引起的。因此,扭转方向的风荷载可采用与横风向相同的数学模型[9-11]。由文献[9]和[11]可知,在扭转方向,根据随机振动的理论,并基于如下假设:

(1) 准定常理论:

(1)

(2)

(3) 脉动风速谱fy(ω),与高度无关:

nSv(n)=fy(ω)

(3)

由此可得,作用在结构上的第一阶广义气动力谱密度SF1(n)为

(z,z′)dzdz′=

(4)

式中:CL为均方根升力系数;fy(ω)为规格化后与高度无关的风力谱密度函数;M1为第一阶的广义质量;B、H为建筑物迎风面的宽度和总高度;VH为H处平均风速;φ1(z)为第一阶振型;β为振型指数;ω为自振圆频率;α为平均风速剖面指数;Jz(α,β)2为竖向联合接受函数,R(z,z′)为扭转方向风荷载的竖向相干函数,表达式如下:

(5)

式中,α1和α2具体取值见表1,简化起见本文假定α1等于0。

表1竖向相干函数α1、α2取值

Table 1α1、α2 in the vertical coherence function

注:D为建筑物平面的总长度

(6)

式(6)中第一项ΦI是对广义扭转力矩的修正,一般情况下,实际振型的广义扭转力矩比较容易计算,这里不予考虑,只对的第二项ΦT,即扭转方向广义气动力谱修正系数定义为

(7)

1.2 参数分析

在式(4)中,各个参数的取值范围如下:α=0.12和0.30,β=0～2,H=100～400 m,B=20～50 m,根据数值积分的原理可得出公式(4)的结果,下面通过图形说明α、β和t对修正系数ΦT的敏感程度,图中t=H/(α2B),范围取0～10,用以代表结构长细比(H/B)的影响。图1给出了不同长细比的广义气动力谱修正系数;图2给出了不同振型指数的广义气动力谱修正系数。

图1 不同长细比的广义气动力谱修正系数Fig.1 Correction factors for generalized aerodynamic spectrum with different slenderness ratios

图2 不同振型指数的广义气动力谱修正系数Fig.2 Correction factors for generalized aerodynamic spectrum with different modes indexes

对于广义气动力谱修正系数ΦT,从图1和图2中可以得出如下结论:

(1) 对于固定的α、β值,修正系数随着长细比的增大而逐渐增大,但增大范围不大,一般在0.1左右;对于固定的α、t值,随着β的增加,修正系数逐渐减小。

(2)β=0(理想模态)时,修正系数恒等于1;在β>0时,修正系数均小于1,也即在扭转方向,理想振型的广义气动力谱均大于实际振型的广义气动力谱,计算结果是偏保守的。

(3) 在α=0.12和0.30,β=0～2和t=0～10情况下,修正系数最大值为1,最小值为0.16,与理想振型下的“1”相比,误差较大,因此建议在扭转方向,对实际振型的广义气动力谱进行修正,以免过大地估算结构的等效静力风荷载。

1.3 广义气动力谱修正系数拟合

由公式(4)可知,修正系数ΦT与参数α、β、B和H都是有关的,在数值积分时本文考虑了这四个参数的影响,但考虑到公式的简洁性,本文在修正公式里面忽略了B和H的影响。根据修正系数和参数α、β的规律,公式(4)最终拟合结果为

(8)

图3给出了α=0.12和0.30时拟合公式的两种结果,图中散点代表计算数据,作为比较也展示了Xu[12]和Holmes[13]的拟合曲线。从图3可看出,本文提出的拟合结果总体上与文献[12]、[13]较为接近,由于考虑了宽度B和总高度H的影响,总体上略有差异。

图3 广义气动力谱修正系数Fig.3 Correction factors for generalizedaerodynamic spectrum

2 基于规范振型的建议

在扭转方向,由《建筑结构荷载规范》(GB 50009—2012)[14]可知,高层建筑基本振型的表达式为

φθ=ξ0.8

(9)

式中:ξ=z/H为相对高度。

由此可知,高层建筑在扭转方向的基本振型并非理想的振型(β=0.8≠0),当采用规范给出的振型计算结构的风致响应时应当予以修正,根据式(5)的拟合结果,表2给出了不同地貌下α=0.12、0.15、0.22、0.30时具体的广义气动力谱修正系数。由表2可知,修正系数变化范围为0.42～0.50,本文保守建议取常数0.50进行修正。

表2基于规范振型的修正系数

Table 2Correction coefficient based on the code mode

3 典型工程算例分析

以珠海某一超高层建筑为例,采用刚性模型测压试验的数据验证了本文提出公式的可靠性。主要参考指标ΔT定义如下:

×100%

(10)

图4给出了振型指数β=0.5和β=1.5时,分别按本文、Xu[12]和Holmes[13]方法修正后的广义气动力谱密度的误差百分比。从图中可知,与Xu和Holmes的方法相比较,按本文方法修正的广义气动力谱密度总体上与实际值相差较少。

4 结 论

在扭转方向,本文研究了非理想振型对于高层建筑广义气动力谱的影响,得到的主要结论如下:

(1) 根据脉动风荷载沿高度分布的相干函数、平均风速剖面指数α、建筑高度H以及迎风面宽度B,运用数值积分的方法,计算得出了振型指数为β的广义气动力谱与理想振型的广义气动力谱比值。同时,结合平均风剖面指数α和振型指数β,拟合出了非理想振型广义气动力谱的修正公式:

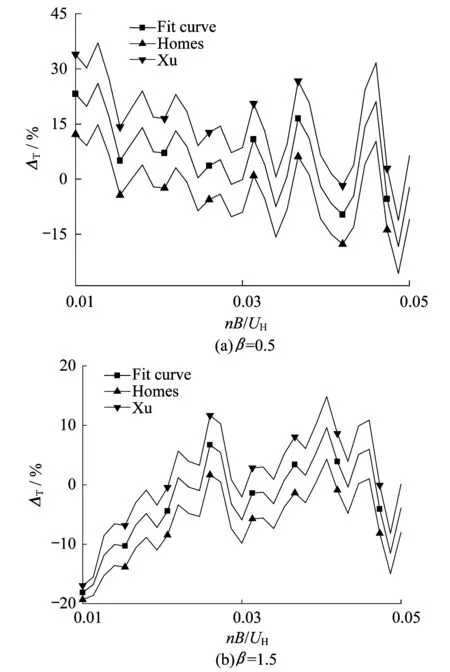
图4 广义气动力谱密度的误差百分比Fig.4 Error percentage of generalized aerodynamic spectrum density

(11)

(2) 在扭转方向,广义气动力谱的修正系数均小于1。实际振型的广义气动力谱低于理想振型的广义气动力谱,实际振型的计算结果均是偏于保守的。基于理想振型得到的广义气动力谱,采用0.5的修正系数进行修正,可应用于建筑结构荷载规范所采用的振型。

(3) 对于固定的α、β值,修正系数随着长细比的增大而略微增大;对于固定的α、t值,随着β的增加,修正系数逐渐减小。