基于多元非线性回归分析的Cu-Ag合金偏析预测模型研究

孟志军，胡茂良，牛连杰，王晔

（1. 西安诺博尔稀贵金属材料有限公司，西安 710201；2. 哈尔滨理工大学 材料科学与工程学院，哈尔滨 150008；3. 河北建筑工程学院 数理系，河北 张家口 075000）

Cu-Ag合金是典型的二元共晶体系合金，铜银合金拥有优异的机械性能、较高的硬度、非常优良的导电和导热性能以及较好的耐磨性。未来高速列车用接触线材、强磁场磁体系统、脉冲强磁场线圈以及大规模集成电路引线框架等方面将会优先选择潜在导体材料[1—3]，同时该材料也是电机换向器和接触线的理想材料，也常常用作高压器件和大电流继电器的接点材料[4—6]。铜银基合金制备的电接触材料在电力系统、电器工业中发挥着比较重要的作用[7—9]，在焊接过程中也展现出了优良的流动性和浸润性，此外铜银合金也广泛应用于航天工业中高温合金和陶瓷之间的焊接钎料[10]，由于其应用前景非常广阔，近年来已经得到了研究者们的广泛关注。显然 Cu-Ag合金的铸态显微组织将决定材料的各方面性能，因此制备出组织成分均匀的铸件是获得材料高强高导性能的关键[11—12]，因此，如何快速而又准确地预测Cu-Ag合金中常出现的成分偏析缺陷，已成为铸态 Cu-Ag合金生产中的重要环节。

随着计算机技术的发展，铸件缺陷的预测和相关数据的分析已经在科学研究和工业生产中扮演着越来越重要的角色。根据大量数据对铸件质量进行准确和有效预测，能够为工艺参数的调整和控制提供高效、可靠的依据[13]。此外，作为一种应用比较广泛的统计模型，多元回归分析对于解决铸造生产过程中的缺陷预测问题来说，是最佳的选择[14]。与传统方法相比，该方法具有简便、快捷、可靠和准确的特点，同时回归分析能够建立出表达各类工艺参数与最终目标相互关系的函数关系式，从而可以直接通过计算获得与真实值接近的预测值，而且不受给定试验样本的范围限制[15]，更重要的是，该方法还能够自动略去试验样本数据中那些不稳定的数值[16]。近十年来，许多学者采用多元回归分析方法对铸件质量和性能进行预测并优化铸造过程中的参数。V. D. Tsoukalas根据多元线性回归分析和遗传运算方法提出了一种有效方法，并通过这种方法针对压力铸造AlSi9Cu3合金中的缩孔问题进行了工艺参数的优化[17]。M. Abdel Aziz通过实验设计方法研究了 AA6063-(TiC/Al2O3)合金的腐蚀特性，并根据线性回归分析建立了回归方程，其实验结果与回归方程的预测结果一致[18]。M. S. Huang和T. Y. Lin基于回归模型提出了一种稳健优化方法，该方法能够有效减少干扰因素对喷射成形过程的影响[19]。舒大禹等采用正交试验对Ti8LC合金的热处理制度进行了设计，并对Ti8LC合金的热处理工艺与抗拉强度进行了回归分析，建立了热处理制度与抗拉强度之间的回归方程[20]。David Hudaka和 Murat Tiryakioglub运用线性回归分析方法和概率估计量，比较了两种类型形状参数（威布尔模数）的无偏估计[21]。D. P. Mondal等通过线性回归分析建立了Al-Zn合金铸件中外加载荷、磨损尺寸、Zn元素浓度以及各参数之间的交互作用与磨损速率之间的函数关系式[22]。凌成智采用多元回归拟合配合改进的模拟退火算法，进行工艺参数的优化，获得了较好的优化效果[23]。

综上所述，目前回归分析方法的研究已在生产成本和质量控制中进行了广泛的应用，并取得了良好的效果，因此，文中将直接采用回归分析方法以及数值模拟技术对 Cu-45Ag合金金属型铸件的偏析缺陷进行研究，获得主要凝固参数与 Cu-45Ag合金铸件偏析缺陷之间的定量关系，为合理优化铸造工艺参数提供理论支撑。

1 试验方法

1.1 材料及物理性能

所采用的合金为 Cu-45Ag二元过共晶合金，二元合金的相图见图1，可以看出，该二元合金的共晶点在Ag的原子数分数为39.9%时发生共晶反应，共晶的反应温度为779.3 ℃，则可以明确本实验所采用Ag-55%Cu（质量分数）二元过共晶合金的固相线温度为779.3 ℃。过横坐标Cu的质量分数为55%的位置作垂线，与相图中的液相线交于一点，过该点做水平线与温度轴的交点为885.8 ℃，该温度即为过共晶合金的液相线温度。对材料的热物性参数进行查找和实际测定，获得的铸件的热物性参数见表1。铸型采用铸铁，其相应的热物性参数可直接通过模拟软件的数据库来选择。

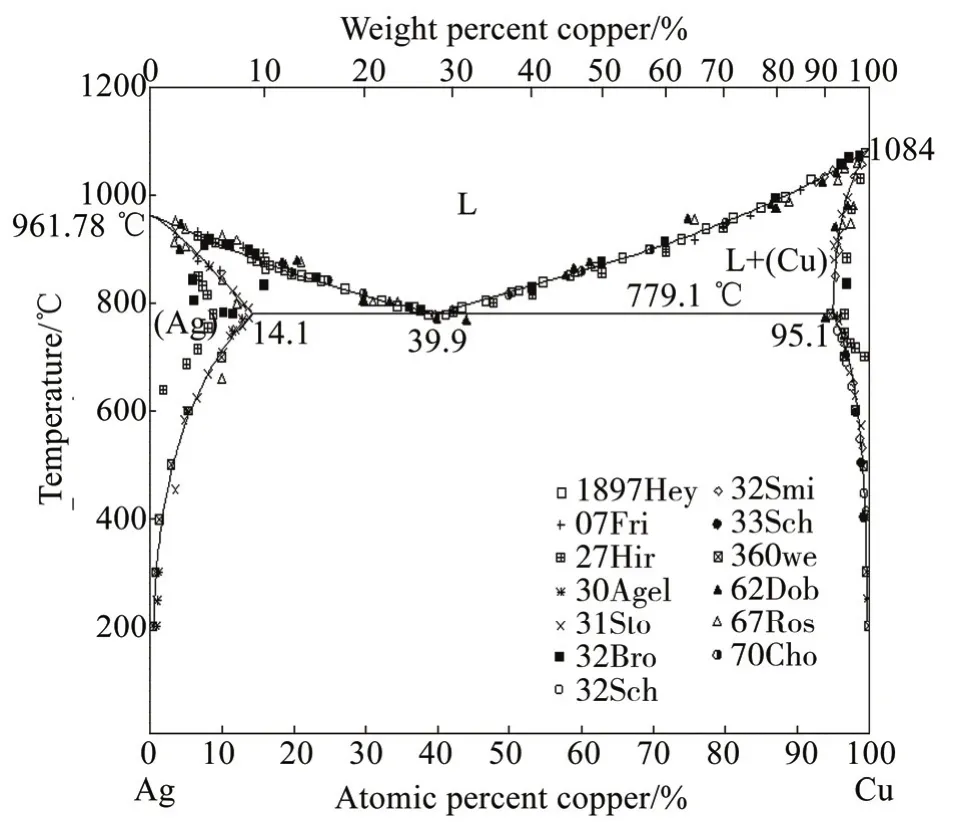
图1 Ag-Cu二元合金相图Fig.1 Phase diagram of Ag-Cu binary alloy

表1 Cu-45Ag二元合金的热物性参数Tab.1 Thermophysical parameters of Cu-45Ag binary alloy

1.2 模型的建立

铸件和铸型三维造型以及网格剖分结果的示意图见图2，采用Solid Works三维造型软件对挤压铸造的铸件/铸型系统部分进行三维造型，造型方法为实体造型，所获得的三维实体包括铸件、涂层以及铸型部分，然后将各个部分在软件中进行装配，并将装配好的文件和各部分分别保存为扩展名为 step的文件。实际铸件将在金属型中进行浇注，铸锭的尺寸为厚34 mm，宽125 mm，高260 mm。浇注过程采用顶注式浇注，不再单独设置浇冒口，如图 2a所示。有限元网格的剖分结果见图 2b，其中铸型的网格长度为8 mm，铸件的网格长度为2 mm，总网格数约为170万个。

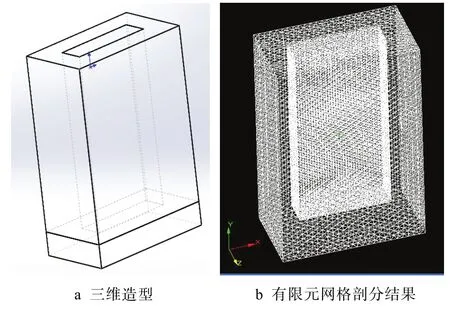
图2 铸件的三维模型Fig.2 3D-model of casting

1.3 R.G.L开放模块

ProCAST模拟软件在其后处理模块中提供了一个可供用户自行设计判据的求解器，即R.G.L开放模块，模块中的求解器主要针对主要凝固参数进行设计和计算，即该模块可直接计算出冷却速率、温度梯度、凝固速率这3个主要凝固参数，并根据用户需求，通过其提供的开放公式进行计算和预测模型的开发，开放公式见式(1)。

式中：M为所建立预测模型的评价值，即因变量；U为凝固速率；G为温度梯度；R为冷却速率；a,c,d为常数。

显然对于偏析缺陷而言，其主要形成于合金凝固的糊状区内，因此判据公式中所需要的各凝固参数的计算就应当确定在这个温度范围内，温度梯度和凝固速率的计算则需要在特定的温度点下进行。根据图1给出的 Cu-Ag的二元相图，各凝固参数的选取温度范围和取值分别由式(2)和式(3)给出。

式中：TL为液相线温度；TS为固相线温度；Tupper和Tlower则分别表示计算冷却速率温度范围的上限值和下限值；TR,G为计算凝固速率和温度梯度所给定的温度值。文中将基于这一开放模块，对相应缺陷的预测模型进行相应的研究和建立。

1.4 多元非线性回归分析

作为一种常用的数据分析统计处理模型，多元非线性回归分析在工程中的应用非常广泛，是研究解决零件生产中制造工艺参数与产品质量相关关系的一种强有力的数理统计方法。与其他方法相比，该方法不仅同样具有简捷方便、精确度和可靠性高等特点，而且还能建立合适的函数关系式来表明各个工艺参数与产品质量之间的相互联系[13—17]，该方程可以突破试验设计对工艺参数范围的限制，从而得到理想的优化工艺参数，因此将通过这种工程统计学的方法，分析研究Cu-Ag合金金属型铸造过程的凝固参数与宏观偏析缺陷之间的定量关系，最终获得快速预测该缺陷且具有工程统计学意义的数学模型，从而达到指导实际生产过程、提高铸件质量、减少试制时间的目的。

采用专业数据处理软件 SAS软件对模拟计算所获得的数据进行多元非线性回归分析，分析过程分为以下几个步骤： ①模型假设，首先对回归方程的形式进行假设，这部分将主要参考一些宏观偏析缺陷预测的模型； ②参数估计，在SAS软件中进行编程，给出假设的回归方程，计算出相应参数的估计值，多元非线性回归采用最小二乘法进行估计； ③显著性检验，软件运行后，将在结果中直接输出显著性的检验结果，根据结果对所假设的模型进行评价； ④模型修正，如果步骤①中假设的模型没有通过检验，则需要对回归方程的形式进行修正，并重复上述步骤，直到回归方程通过检验为止； ⑤试验验证，通过实际试验结果对回归方程的适用性进行验证。

2 结果与讨论

2.1 主要凝固参数

由于凝固过程中的凝固参数主要有凝固速率、温度梯度和冷却速率，而凝固速率可以通过温度梯度和冷却速率来进行表示，因此，采用温度梯度和冷却速率这2个主要凝固参数来进行宏观偏析的预测。在仿真过程中在铸件表面进行选点，选点位置及编号见图3。分别在铸件正面、左侧以及上下部 4个表面位置选取特征点中上表面的特征点命名为T1～T3，下表面的的特征点命名为 B1～B3，正面的特征点命名为Z11～Z34，左侧特征点的命名为C1～C4，所有的特征点均匀分布。

图3 各参考点的选取Fig.3 Position of each reference point

为了获得实际铸件的宏观偏析缺陷的产生情况，采用浇注工艺参数：浇注温度为1100 ℃、浇注时间为30 s、铸型温度300 ℃、涂料厚度1.0 mm进行实际浇注，浇注完成后，利用直读光谱分析仪对铸件进行Ag含量的分析，分析的位置与图3给出的特征点位置相一致。利用 ProCAST采用相同的工艺参数进行铸件充型和凝固过程的模拟，计算完成后对计算结果中对各个面上的特征点位置进行温度梯度和冷却速率数值提取，所获取的各特征点的凝固信息与 Ag含量见表2，所给出的温度梯度单位均为K/cm2，冷却速率单位均为K/s。

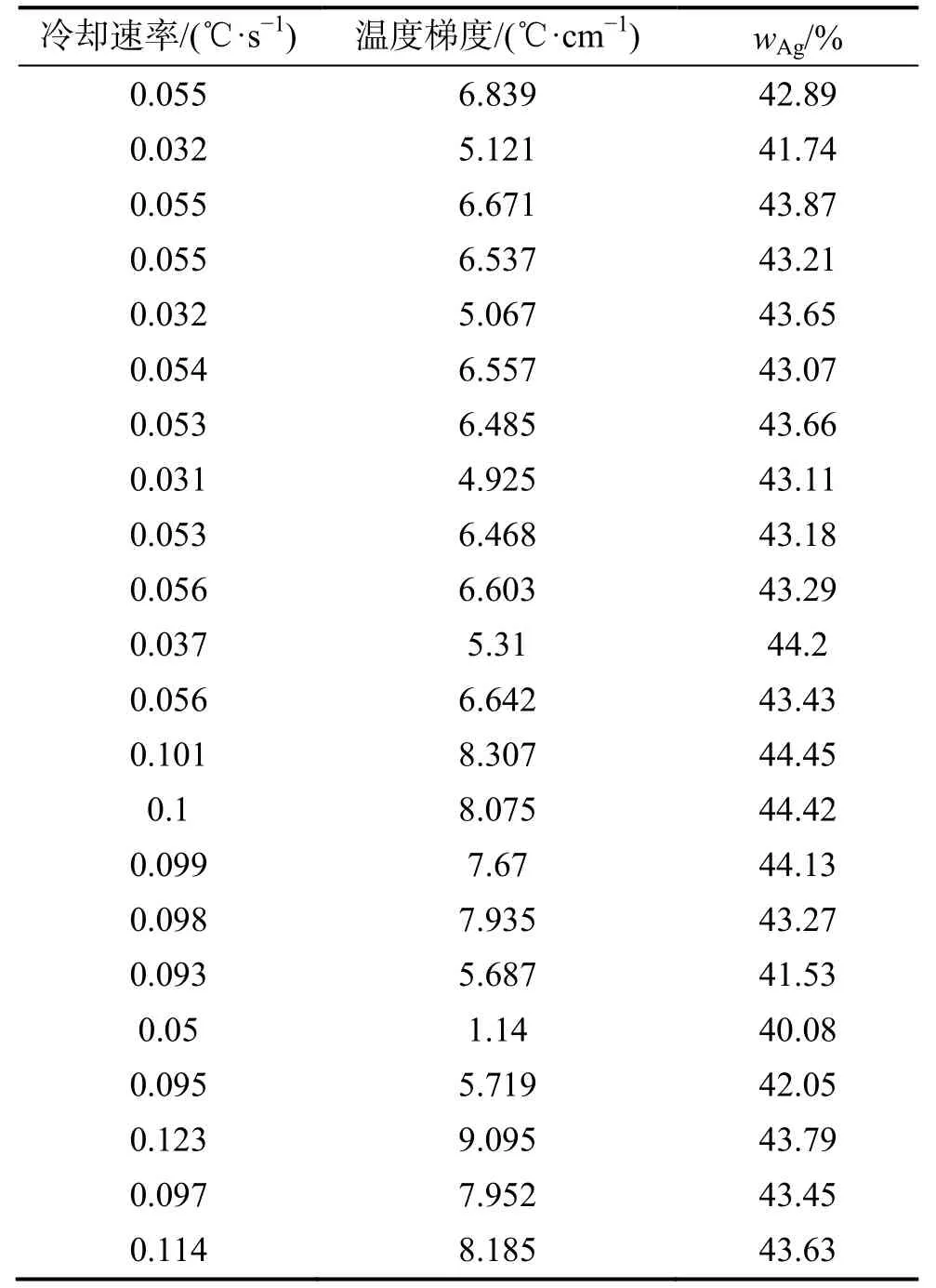
表2 特征区域部位的凝固信息和Ag的质量分数Tab.2 Solidification information and Ag content of feature areas (mass fraction)

2.2 回归分析

通过表2列出的实际浇注与数值模拟计算结果，可以看出对于上表面的凝固信息而言，其冷却速度与侧边相近，但温度梯度较小，而产生了较大的宏观偏析缺陷。铸件正面上部的各个特征点的冷却速度和温度梯度均较小，也同样产生了较大的宏观偏析，因此，可以认为冷却速度和温度梯度越小，越容易产生宏观偏析，且温度梯度对宏观偏析的形成影响更大。通过对数据进行拟合，得到的回归方程见式(4)。

式中：A=40.256 26,B=0.017 27。该表达式与文献[24]所报道的在Al-7%Si合金铸件中进行宏观偏析预测的判据形式相类似。此外，从模型中也可以看出，由于温度梯度G的指数为2，因此温度梯度对宏观偏析形成的影响比冷却速度要大。

回归模型的显著性检验结果和参数估计的显著性检验结果分别见表3和表4。可以看出，不管是F检验还是t检验的p值均能够满足回归方程(4)：p＜0.0001＜α。可见，提出的模型很好地符合表2中所列出的实测数据。

表3 回归模型的显著性检验Tab.3 Analysis of Variance for model

表4 回归模型的参数估计的显著性检验Tab.4 Significance testing for parameter estimation of regression model

3 工艺改进和试验验证

根据宏观偏析预测模型，可以在实际浇注之前的前期模拟计算中对Ag元素的含量进行大致的预测，从而判断Cu-Ag合金中宏观偏析的大致位置和程度。为了对 Cu-Ag合金的浇注工艺进行改进，分别对影响冷却速度和温度梯度的主要浇注工艺参数，即浇注温度、浇注时间（浇注速度）、铸型温度和涂料厚度分别进行单因素调整模拟试验。计算结果表明，浇注时间（浇注速度）对主要凝固参数的影响较大，浇注温度、铸型温度和涂料厚度的影响较小。此外，降低浇注速度可以有效提高冷却速度和温度梯度，从而有效减小宏观偏析的倾向。

在通过确定最佳浇注工艺参数的同时，为了对模型的准确性和实用性进行验证，采用模拟后获得的最佳浇注工艺方案进行浇注，即浇注温度为1100 ℃、浇注时间为120 s、铸型温度为200 ℃、涂料厚度为1.5 mm，并对实际浇注获得的铸件进行检测，结果表明，通过最优浇注工艺参数获得铸件中的宏观偏析缺陷已经得到明显的改善，测量获得的数值与预测的数值基本接近，均位于预测优化的数值范围之内。

4 结论

通过采用多元非线性回归方法和数值模拟对Cu-45Ag合金金属型铸造过程产生的宏观偏析缺陷的预测模型进行研究，并根据获得的回归模型进行了相应的仿真研究和工艺改进，通过对试验结果的分析研究，得到了以下结论。

1)通过回归分析方法，获得的Cu-45Ag合金金属型铸造宏观偏析的数值模型为：

通过对回归模型和参数估计的显著性检验结果进行分析，表明该方程能够很好地表达主要凝固参数与宏观偏析之间的对应关系。

2)针对优化工艺参数进行计算，其结果表明，浇注时间（浇注速度）对主要凝固参数的影响较大，浇注温度、铸型温度和涂料厚度的影响较小。降低浇注速度可以有效提高冷却速度和温度梯度，从而有效减小宏观偏析的倾向。

3)获得的最佳浇注工艺方案为浇注温度1100 ℃、浇注时间为120 s、铸型温度200 ℃、涂料厚度 1.5 mm。采用该方案进行实际浇注，对所获得铸件的检测结果表明，铸件中的宏观偏析缺陷得到了明显的改善，验证试验的结果还同时表明，提出的宏观偏析预测模型能够有效对 Cu-45Ag合金金属型铸件进行偏析预测，为工艺设计人员进行合理的工艺优化提供帮助。