Micro-CT系统的设计

鄢苏鹏，刘正明

解放军第一医院 医学工程科，甘肃 兰州 730000

引言

Micro-CT（也称为显微CT）被定义为测定体素的空间分辨率小于100 μm的CT系统[1]。它采用了与普通临床CT不同的微焦点X线球管，分辨率高达几个微米，具有良好的“显微”作用[2]。Micro-CT能够在不破坏样品的情况下，对骨骼、牙齿、活体小动物和各种材料器件进行高分辨率（＜10 μm）X线成像，获取样品内部详尽的三维结构信息，从而显示各部分的三维图像，分辨率远远高于临床CT[3-5]。除了生物学、医学、新药开发和材料学的应用之外，Micro-CT还广泛应用于工业、农业、工程、珠宝、古生物学和考古学等领域[6]。

目前市面上的成品Micro-CT系统，多是用来对离体组织或者活体小鼠成像，成像视野小，管电压小，不能对大动物或大物体进行成像[7]。而本研究就是要设计一种大视野、大管电压的Micro-CT系统，用于兔子的成像。Micro-CT一般包括X线管、探测器和机械装置等[8]。Micro-CT的基本原理是：X射线源连续的产生锥形束X射线，穿过载物台上的被测物体，在探测器上成像。探测器后端连接电脑数据采集系统，旋转一周依次得到被测样本在不同角度下的二维投影图像序列。对得到的投影序列根据需求进行图像预处理，之后对投影图像序列进行断层重建，得到断层图像序列。将断层图像序列使用各种可视化方法显示出来。

1 系统的硬件设计

1.1 系统类型

Micro-CT系统主要由X射线源、X射线探测器和机械扫描结构等3部分组成，并由一台计算机作为控制处理单元实现系统的整体控制[9]。根据系统的机械结构的不同，将系统分为转台式和转桶式两种，见图1。两种系统类型的对比，见表1。

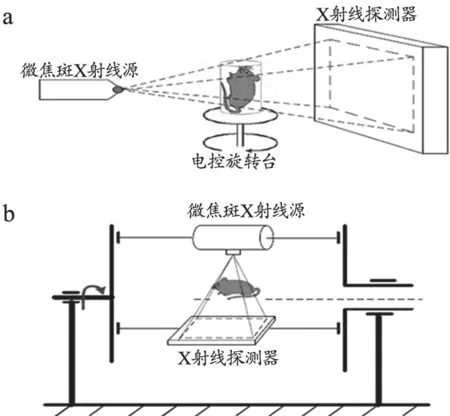
图1 Micro-CT的机械扫描结构转台式（a）转桶式（b）

表1 两种系统类型的比较

在我们设计的系统中，采用转台式的扫描方式。利用一个电控旋转台，控制物体的旋转，利用多个电控位移台，实现物体的前后左右的移动。这样不仅实现方便，调整简单，而且能达到较高的空间分辨率[2]。

1.2 X线管和探测器的选择

系统所能达到的最高空间分辨率受到系统焦斑大小、探测器像素大小、机械稳定性、系统几何放大倍数、重建算法等多种因素的影响，其中设备的硬件参数起着更为决定性的作用。设X射线源的焦斑大小F，探测器像素大小d，用SDD和SOD分别表示X射线源到探测器中心和到物体的距离，参见图2，定义系统的放大倍数为M=SDD/SOD，则射线的等效束宽BW[2]可表示为：

BW从物理上确定了系统可能达到的极限分辨率。

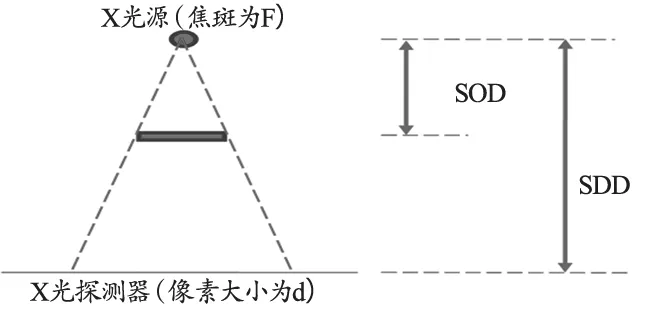
图2 Micro-CT系统几何位置示意图

X线管在选择时，管电压在足够大，能够穿透兔子的情况下，焦点的大小要尽可能小，以使成像的结果尽可能好，3款均满足要求（表2）。

表2 不同的X线管

探测器在选择时，因为要保证大视野（大于10 cm），所以探测器的尺寸要大，而且探测器像素的大小要尽量小，以使确保成像质量，同时读出速率也不能低，不然采集时间过长，照射剂量太大，导致兔子死亡，会使活体成像没有意义，3个测试款探测器均满足要求（表3）。

将以上的X线管和探测器两两组合起来，选定视野直径为15 cm，计算其系统的极限空间分辨率，见表4。

可以看出来，L9421-02和2923的组合，其保证15 cm视野的情况，系统的极限空间分辨率在这些组合里是最小的，但是考虑到成本的问题，我们选择了Ultrabright 90和2321，系统能达到的最小空间分辨率为49.2423 μm，能够实现高分辨率、大视野的目标。

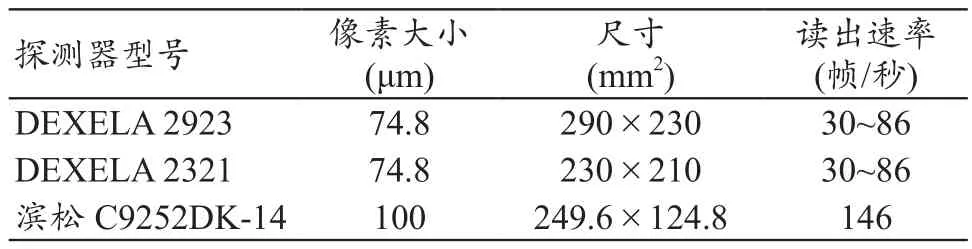
表3 不同的探测器

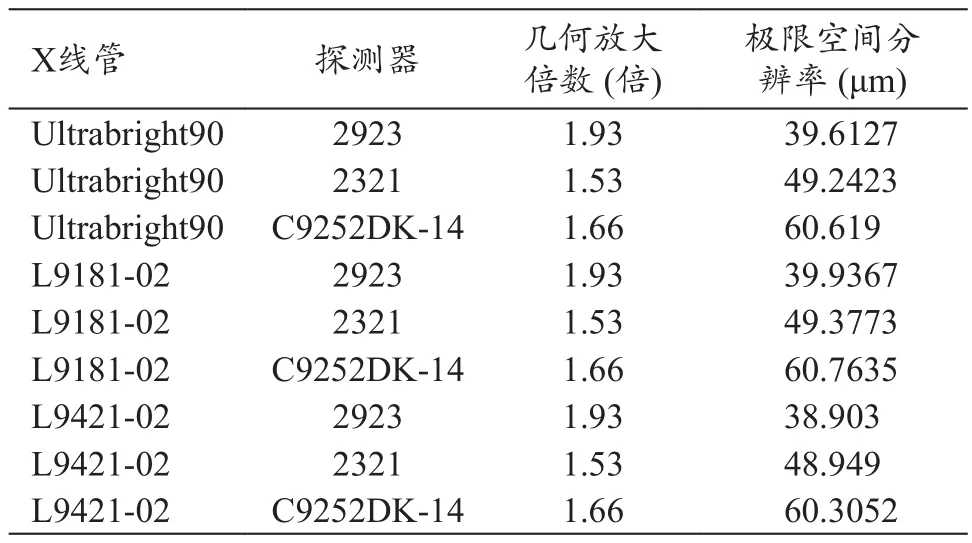
表4 不同X线管和探测器组合系统极限空间分辨率的情况

1.3 SOD和SDD的设计

源到物体的距离SOD和源到探测器的距离SDD是系统的安装时必要考虑的两个量，它们决定了源、物体、探测器之间的相对关系。当探测器尺寸一定且需要的视野一定时，则系统的几何放大倍数M就确定了，则SDD/SOD的值也确定了。但如果SDD太大的话，会使到达探测器的X线光子数目减少，降低对比度分辨率[9]；如果SDD太小，为保证重建结果，锥角控制在10°以下，则视野变小，探测器成像面积没有有效利用。

如图3所示，为了有效利用探测器的面积，而且为了保证成像质量，要求锥角θ小于10°[10]，所以SDD、θ、探测器宽度A满足如下关系：

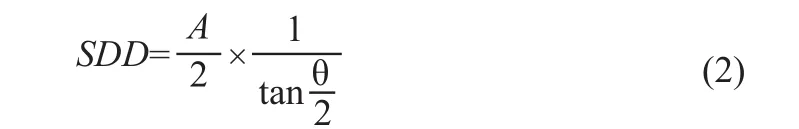
图3 计算SDD的示意图

2 系统的软件设计

2.1 FDK重建算法

FDK算法，它由Feldkamp等[11]在1984年提出，因其易于实现、执行效率高等优点，在圆轨道锥束CT中广泛应用。FDK算法是一种解析的近似重建算法，在锥角比较大的时候存在锥束伪影，为了解决锥束伪影问题，很多人提出了改进的FDK算法[12]。在锥角比较小的情况下，FDK重建结果比较好。使用FDK 算法重建时，必须在360°扫描范围内具有充足的投影数据，否则图像中将产生伪影[11]。

锥束CT扫描几何结构，见图4。设射线源到旋转中心的距离为R，射线源到探测器距离为D，称射线源到探测器中心且与探测器垂直的射线为中心射线，FDK算法重建公式为：

其中gI(u,v,λ)代表投影数据，λ为投影角度，（u,v）为虚拟探测器的横、纵坐标；ξ为从射线源出发过点x→的射线与中心射线的夹角，斜坡函数；； 反 投 影 需 要 加 权

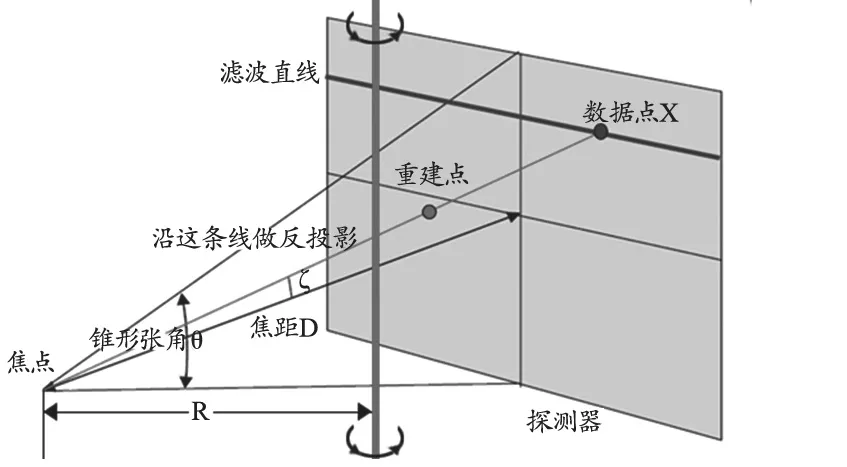
图4 锥形束重建算法的坐标系

2.2 程序流程及各模块说明

（1）预处理。对各数据点做预处理，乘以cosξ，ξ是指数据点到源的连线和中心点到源的连线的夹角。

（2）滤波。若选择no filter（无滤波器），则只进行算法中的斜坡滤波，如果选择滤波器，则还要使用用户选择的滤波器对数据进行滤波，滤波均是通过卷积实现[13]。

（4）输出。重建完成之后，根据用户输入的路径保存重建图像，同时可以在程序右上方浏览各层的图像，还可以将各层图像保存。

2.3 重建结果展示

重建程序，见图5。投影数据使用3D phantom模型（3D SHEPP-LOGON模型）仿真投影，该模型在CT算法仿真实验和性能评价中被普遍采用[14]。重建后选取的四层图像，见图6。从这四幅图中可以看出，重建算法很好地体现了不同层面之间的不同，而且各层面成像结果也很清楚。

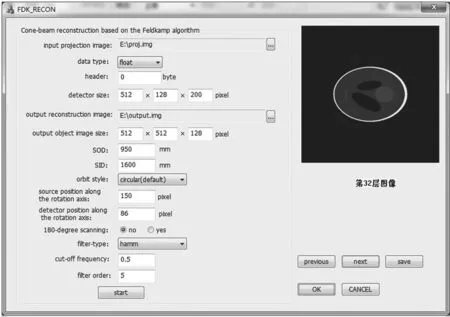
图5 重建程序界面

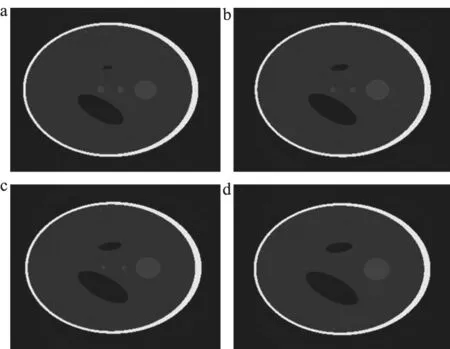
图6 不同层面的成像结果

3 结语

本研究设计的Micro-CT系统，成像视野大，管电压大，能够满足对于活体兔子成像的实验需求，弥补了市面上成品Micro-CT成像视野小、管电压小、价格昂贵、不能满足特定实验需求的缺点。

但因安装过程会导致系统几何位置产生误差[9]，而误差对成像效果有较大的影响，重建图像中将会出现伪影，严重时将导致重建结果没有意义[15]。因此，下一步重点将针对系统安装完成后的几何位置误差，进行校正方法的软件设计与实现。同时，还可对重建算法进行进一步优化，引入并行计算，提高重建速度[16]。

[参考文献]

[1] 桂建保,胡战利,周颖,等.高分辨显微CT技术进展[J].CT理论与应用研究,2009,18(2):106-116.

[2] 朱守平.微型计算机断层成像及其与自发荧光断层成像多模态融合的研究[D].北京:中国科学院自动化研究所,2010.

[3] 王燕芳,王杰,魏存峰,等.锥形束显微CT技术在颞骨成像中的应用及发展[J].中国耳鼻咽喉头颈外科,2015,22(6):280-283.

[4] 许可,李谨.显微CT在评价根管预备效果中的应用[J].口腔医学,2016,36(7):653-656.

[5] 杨曦,徐永清,何晓清.显微CT对小动物血管三维成像的研究进展[J].中国骨与关节损伤杂志,2016,31(3):334-336.

[6] 谷舟,杨益民,齐雪义,等.显微CT技术在古代料珠研究中的应用—以河南淅川县马川墓地出土料珠为例[J].CT理论与应用研究,2014,23(5):797-803.

[7] 刘文磊.低剂量CT成像与稀疏角度重建研究[D].西安:第四军医大学,2013.

[8] 张求德.基于旋转机架的小动物锥束CT系统设计与开发[D].武汉:华中科技大学,2016.

[9] 杨孝全,邓勇,邓子林,等.基于平板探测器的小动物微型CT成像系统[J].中国医疗器械杂志,2009,33(4):255-258.

[10] 张剑,陈志强.三维锥形束CT成像FDK重建算法发展综述[J].中国体视学与图像分析,2005,10(2):116-121.

[11] 李真真,杜明辉.锥形束重构解析算法的研究进展[J].中国生物医学工程学报,2007,26(2):308-312.

[12] 刘辉,张权,刘祎,等.锥束FDK反投影重建算法的三角函数优化[J].计算机工程与应用,2017,53(19):179-183.

[13] 洪振厚,周彬,郭金川.锥束X射线CT图像重建的新型滤波函数[J].深圳大学学报理工版,2017,34(3):284-289.

[14] 曹涵,胡战利,方方.锥束CT系统的3D Shepp-Logan体模仿真及其投影数据重建[J].信息通信,2014,(134):48-49.

[15] 陈炼,吴志芳,刘锡明,等.锥束CT系统几何参数校正的解析计算[J].清华大学学报:自然科学版,2010,(3):418-421.

[16] 郑海亮,李兴东,王哲,等.高分辨锥束CT并行重建算法在基于NVDIA GPU显卡计算平台上的实现[J].CT理论与应用研究,2014,23(5):805-814.