面向属性的区间集概念格*

贺晓丽，魏 玲，钱 婷

1.西北大学 数学学院，西安 710127

2.西安石油大学 理学院，西安 710065

1 引言

形式概念分析[1-2]（formal concept analysis，FCA）是由德国数学家Wille于1982年以重建格理论为目的提出的一种数学理论。它的数据表现形式为二维交叉表即形式背景。形式背景(G,M,I)是一个由对象集G，属性集M以及G与M间二元关系I构成的三元组。在形式背景上，通过一对伽罗瓦连接可以形成概念(X,B)，其中X为概念的外延，是属于这个概念的所有对象的集合；而B为内涵，是所有这些对象所共同具有的属性（或特征）集。概念格是知识的一种表现形式，也是数据处理的一种工具。

形式概念分析与其他理论的融合研究是其理论研究的一个重要方面，迄今为止已产生诸多颇有意义的研究成果。例如，与三支决策理论结合，祁建军等人[3]提出了三支形式概念分析理论；与粒计算理论相结合，Belohlávek等人[4]给出了多尺度形式背景中的概念格构建理论与算法，在此方面更为详细的研究可参看李金海和吴伟志[5]所给出的综述研究；与模糊集理论相结合，Belohlávek[6-8]提出了模糊形式背景和模糊概念格；与粗糙集理论相结合，Düntsch和Gediga[9]提出了面向属性概念格，类似地，Yao[10]定义了面向对象概念格。与描述不完备信息的区间集理论相结合，马建敏等人[11]引入了区间集概念格。其本质思想是把概念中表示外延与内涵的集合推广到区间集，利用区间集所反映的不确定信息把经典概念扩展到区间集概念。随后，对区间集概念格的构造理论进行了研究[12]。在不完备形式背景上，Yao[13]提出了区间集算子，并对李金海等人[14]提出的近似概念格进行了相应的区间集表示。

已经知道，面向属性概念格是粗糙集与概念格相结合的一种数据分析理论，鉴于粗糙集与区间集更为密切的联系，本文拟将区间集思想引入到面向属性概念格框架之中，给出了面向属性的区间集概念格构造方法及相应的建格算法。

本文组织结构如下：第2章回顾概念格、面向属性概念格和区间集等相关定义；第3章提出一对新的伽罗瓦连接，并在此基础上定义了面向属性的区间集概念及面向属性的区间集概念格；进一步研究面向属性概念格与面向属性的区间集概念格之间的关系，同时给出面向属性的区间集概念格的构造方法及相应的建格算法；第4章进行了总结和展望。

2 基础知识

定义1[1]设(G,M,I)为一形式背景，对象集X⊆G和属性集A⊆M上定义了一对对偶算子如下：

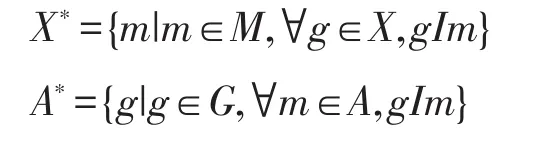
若X∗=A且A*=X，则称(X,A)为形式背景(G,M,I)的一个概念。记形式背景(G,M,I)的所有概念构成的集合为L(G,M,I)，在L(G,M,I)上，定义二元关系“≤”为：

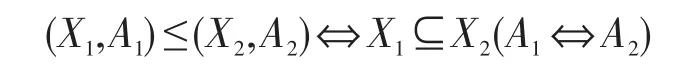
(L(G,M,I),≤)在偏序关系“≤”形成完备格，称(L(G,M,I),≤)为概念格。

定义2[9]设(G,M,I)为一形式背景，↑和↓是2G与2M之间的一对算子，X↑={m∈M|m*⋂X≠∅}A↓={g∈G|g*⊆A}。若X↑=A且A↓=X，则称 (X,A)为面向属性概念。其中，X为面向属性概念的外延，A为面向属性概念的内涵。记形式背景(G,M,I)的所有面向属性概念构成的集合为PL(G,M,I)。在PL(G,M,I)上，定义二元关系 ≤ 为：(X1,A1)≤(X2,A2)⇔X1⊆X2(A1⊆A2)。容易证明“≤”是偏序关系且(PL(G,M,I),≤)在偏序关系“≤”形成完备格，即任意的两个概念(X1,A1),(X2,A2)的上确界和下确界为：

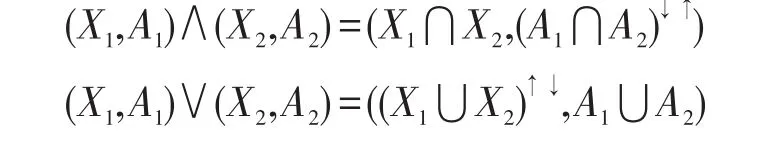
称(PL(G,M,I),≤)为面向属性概念格。

定义3[15]设U是有限论域，2U为U的幂集。定义X=[X1,X2]={XΔ∈2U|X1⊆XΔ⊆X2}，称为U的区间集。对于任意的X∈2U，X可以看成是由区间集[X,X]退化得到的。U上所有的区间集构成的集合记为I(2U)。类似于经典集合之间的运算，Yao给出了区间集间的运算[15]。

定义4[15]设U是有限论域，X,Y是U上的区间集，即X=[X1,X2]，Y=[Y1,Y2]∈I(2U)，定义：

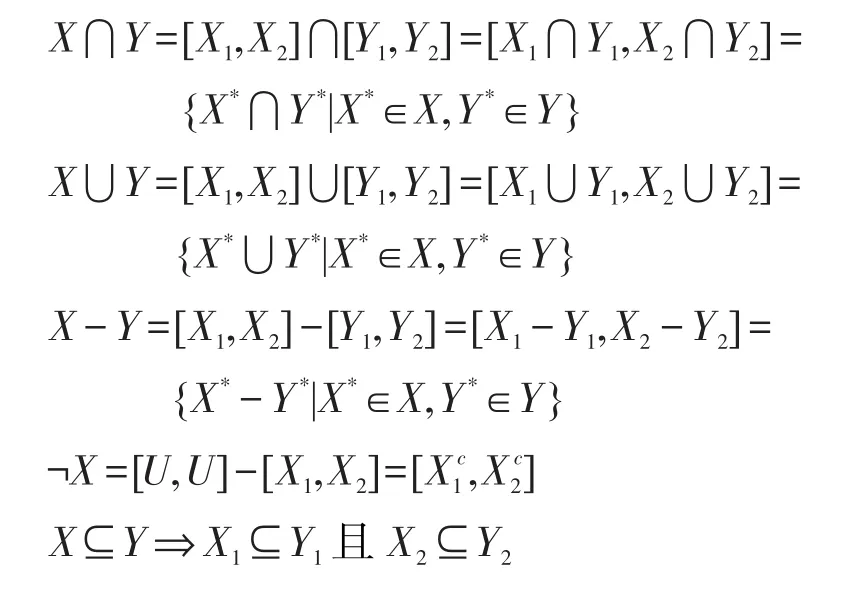
3 面向属性的区间集概念格

3.1 面向属性的区间集概念格的定义

定义5设(G,M,I)为一形式背景，对于任意的X=[X1,X2]∈I(2G)，A=[A1,A2]∈I(2M)，定义I(2G)与I(2M)之间的一对算子⇑:I(2G)→I(2M)和⇓:I(2M)→I(2G)如下：

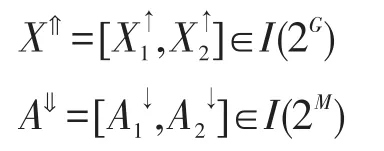
例1(G,M,I)为一个形式背景（如表1所示），其中G={1,2,3}，M={a,b,c}。

取X=[3,13]∈I(2G),A=[c,ac]∈I(2M)，按照定义5，有 [3,13]⇑=[3↑,13↑]=[c,ac]，[c,ac]⇓=[c↓,ac↓]=[3,13]。

Table 1 Formal context(G,M,I)表1 形式背景(G,M,I)

性质1设(G,M,I)为一形式背景，对于任意的X=[X1,X2]∈I(2G)，A=[A1,A2]∈I(2M)，I(2G)与I(2M)之间的一对算子⇑:I(2G)→I(2M)和⇓:I(2M)→I(2G)，则⇑和⇓具有以下性质：

（1）X⊆Y⇒X⇑⊆Y⇑

（2）A⊆B⇒A⇓⊆B⇓

（3）X⊆X⇑⇓,A⇓⇑⊆A

（4）X=X⇑⇓⇑,A⇓⇑⇓=A

（5）(X⋃Y)⇑=X⇑⋃Y⇑,(A⋂B)⇓=A⇓⋃B⇓

证明下面仅证明（5）。

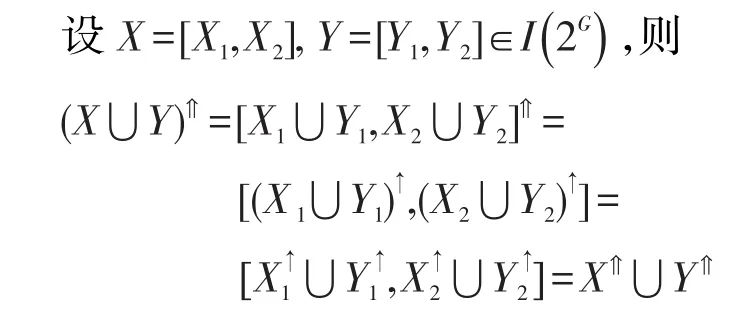
类似可证明(A⋂B)⇓=A⇓⋃B⇓。 □

定义6设(G,M,I)为一形式背景，∀X∈I(2G),A∈I(2M)，若X⇑=A且A⇓=X,则称 (X,A)为面向属性的区间集概念。其中，X称为面向属性的区间集概念的外延，A称为面向属性的区间集概念的内涵。

记形式背景(G,M,I)的所有面向属性的区间集概念构成的集合为PIL(G,M,I)，所有面向属性的区间集概念的外延构成的集合为PILG(G,M,I)，所有面向属性的区间集概念的内涵构成的集合为PILM(G,M,I)，定义PIL(G,M,I)上的二元关系为：(X,A)≤(Y,B)⇔X⊆Y(A⊆B)。

很容易证明上述的二元关系“≤”是偏序关系且在此偏序关系下，PIL(G,M,I)形成完备格，即对任意的两个概念(X,A)、(Y,B)的下确界和上确界分别如下所示：

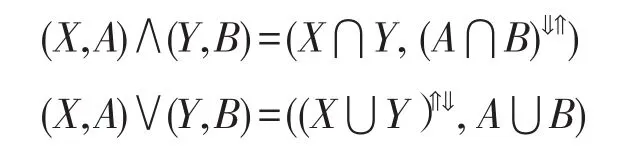
例2（续例1） 因为X=[3,13],A=[c,ac]，由例1知X⇑=[c,ac]=A,A⇓=[3,13]=X，所以由定义6知 (X,A)是面向属性的区间集概念。类似地，可以求出此形式背景的所有面向属性的区间集概念及其相应的面向属性的区间集概念格PIL(G,M,I)。格图如图1所示。

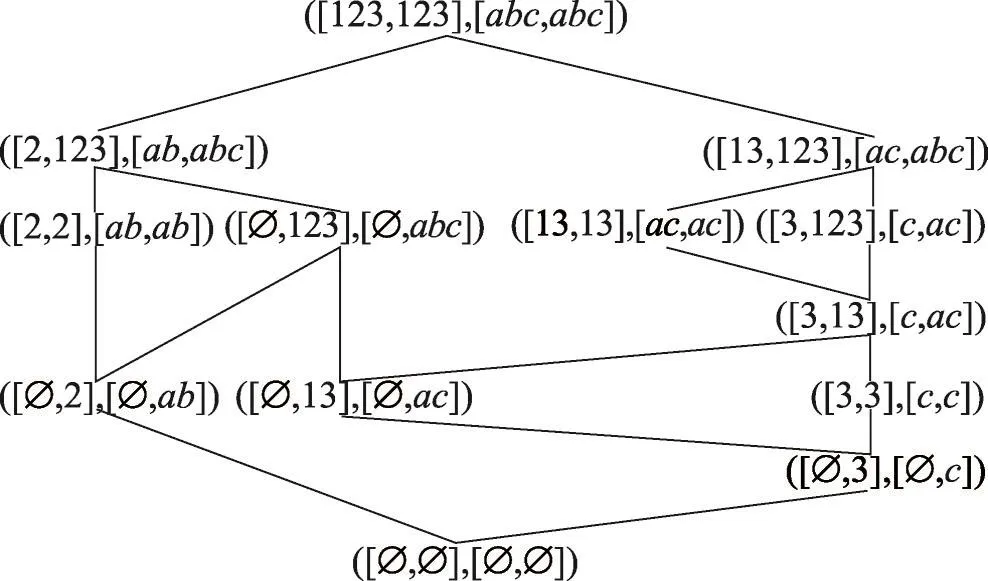
Fig.1 Property oriented interval-set concept lattice of Table 1图1 表1的面向属性的区间集概念格

3.2 面向属性概念格与面向属性的区间集概念格的关系

本节从元素、集合及代数结构的角度研究面向属性概念格与面向属性的区间集概念格之间的关系。

为了研究集合PIL(G,M,I)与集合PL(G,M,I)之间的关系，记：

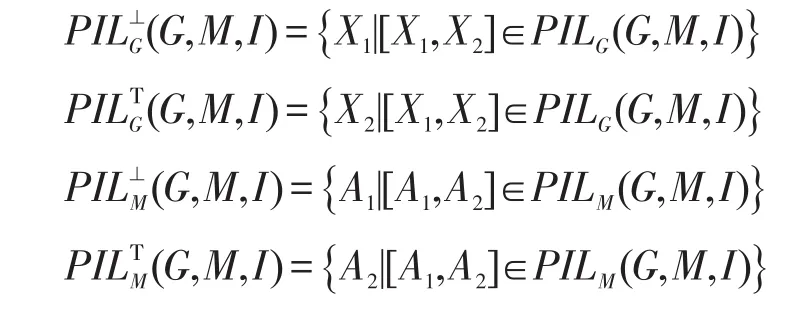
定理3设(G,M,I)为一个形式背景，PL(G,M,I)为其相应的面向属性概念格，PIL(G,M,I)为其相应的面向属性的区间集概念格，则下列式子成立：

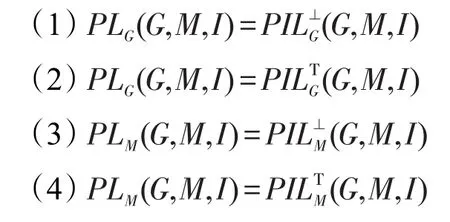
上面定理1及定理2从元素上研究了面向属性概念格与面向属性的区间集概念格间的关系，而定理3从集合整体上进一步研究了两者之间的关系。下面将从代数结构上探讨两者之间的关系。

定理4设(G,M,I)为一个形式背景，PL(G,M,I)为其相应的面向属性概念格，PIL(G,M,I)为其相应的面向属性的区间集概念格，则存在一个映射f:PL(G,M,I)→PIL(G,M,I)使得f(PL(G,M,I))是PIL(G,M,I)的一个子格。

证明对于任意的(X,A)∈PL(G,M,I)，定义f(X,A)=([X,X],[A,A])。由定理1知 ([X,X],[A,A])∈PIL(G,M,I)，故f是从PL(G,M,I)到PIL(G,M,I)的一个映射。从而f(PL(G,M,I))是PIL(G,M,I)的一个非空子集。下面证明f(PL(G,M,I))对∧，∨封闭。

（1）对于任意的 ℜ1,ℜ2∈f(PL(G,M,I))，存在 (X,A)，(Y,B)∈PL(G,M,I)，使得：

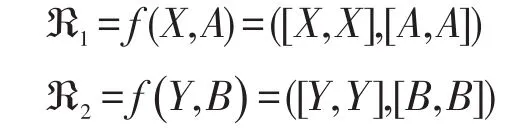
由定义6知：

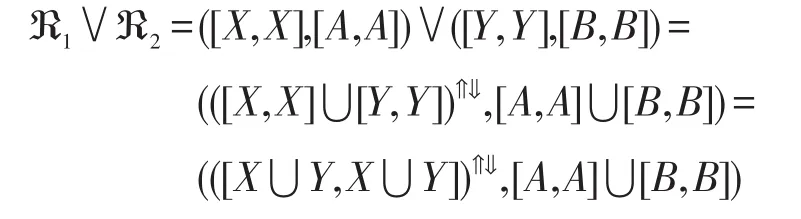
由面向属性概念格中的上确界定义知，对于上述的 (X,A),(Y,B)∈PL(G,M,I)，则 (X,A)∨(Y,B)=((X⋃Y)↑↓,A⋃B)∈PL(G,M,I)，由f的定义知：

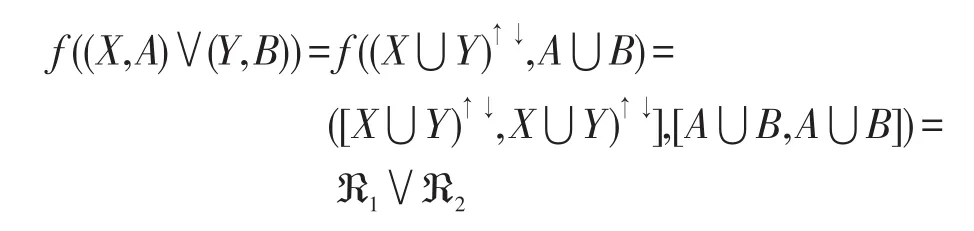
因此ℜ1∨ℜ2∈f(PL(G,M,I))。

（2）对于任意的 ℜ1,ℜ2∈f(PL(G,M,I))，存在(X,A),(Y,B)∈PL(G,M,I)，使得：

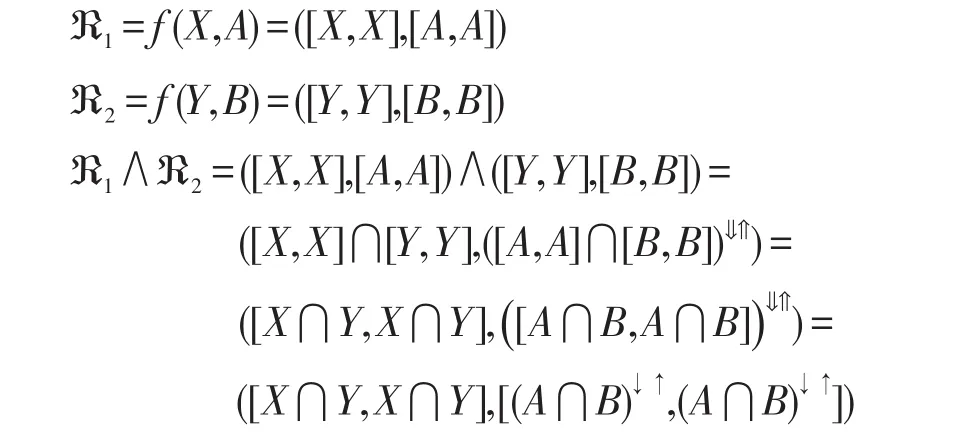
由面向属性概念格中下确界的定义知，对于(X,A),(Y,B)∈PL(G,M,I)，则：

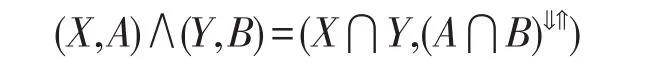
因此，由f的定义知：

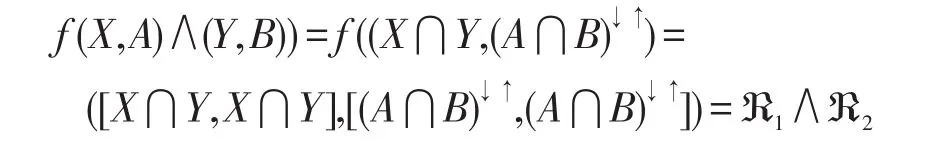
从而，ℜ1∧ℜ2∈PIL(G,M,I)。故f对∧封闭。

综上所述f(PL(G,M,I))是PIL(G,M,I)的一个子格。 □

定理5设(G,M,I)为一个形式背景，PL(G,M,I)为相应背景的面向属性概念格，若对于任意的(X1,A1)，(X2,A2)∈PL(G,M,I)且X1⊆X2，则：

因此(X,A)∈PIL(G,M,I)。 □

3.3 面向属性的区间集概念格的构造

基于上述二者之间的关系，给出面向属性的区间集概念格的构造方法。

定理6设(G,M,I)为一个形式背景，PL(G,M,I)为其相应的面向属性概念格，PIL(G,M,I)为其相应的面向属性的区间集概念格，则：

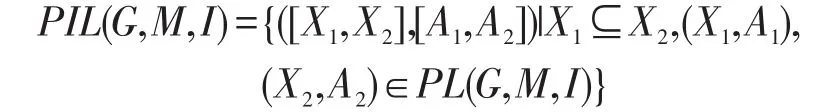
证明记 ℜ ={([X1,X2]，[A1,A2])|X1⊆X2,(X1,A1),(X2,A2)∈PL(G,M,I)}，由定理2知，PIL(G,M,I)⊆ℜ，又由于定理5知ℜ⊆PIL(G,M,I)，故ℜ=PIL(G,M,I)。 □

例3（续例1）利用定理6构造表1的面向属性的区间集概念格。通过定义2可计算出面向属性概念的外延为：并由上述外延构成的区间集有：[∅ ,∅ ],[∅ ,2],[∅ ,3]，[∅ ,13]，[∅ ,123]，[2,2]，[2,123][3,3],[3,13],[3,123]，[13,13]，[13,123]，[123,123]。由定理6知，面向属性的区间集概念有([∅,∅],[∅,∅ ]),([∅ ,2],[∅ ,ab]),([∅ ,3],[∅ ,c]),([∅ ,13],[∅ ,ac]),([∅ ,123],

利用图1，可验证上述所求的面向属性概念正确。依据定理6，给出相应的算法。

算法1面向属性的区间集概念格构造的算法

输入：形式背景(G,M,I)。

输出：面向属性的区间集概念格PIL(G,M,I)。

1.PIL(G,M,I)=∅ ，PL(G,M,I)=∅

2.调用求面向属性概念格的算法[16]计算PL(G,M,I).

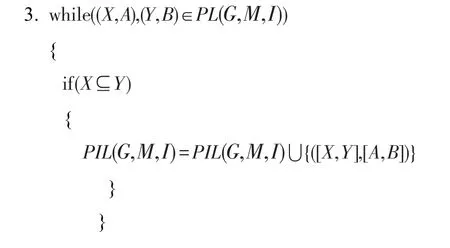
4 总结与展望

本文主要给出了面向属性的区间集概念格的定义，并研究了面向属性的区间集概念格与面向属性概念格之间的关系，最后给出了面向属性概念格的构造方法及其相应的算法。对于本文所提的研究对象，将研究其相应的属性约简及压缩问题，对所获知识进行凝练提取。另外，还可以将此思想引入到其他理论框架中，例如引入到面向对象概念格并研究新型概念格之间的关系。