使用混合差异性度量的分类器选择方法*

米爱中，陆 瑶

河南理工大学 计算机科学与技术学院，河南 焦作 454000

1 引言

多分类器集成的目的是为了获得更好的识别性能，在该项技术的研究过程中，可以很轻松地获取大量分类器集合并通过某种手段进行融合。但是这种做法存在一些弊端：首先随着分类器数量的增加势必会加大存储空间与运行时间的消耗；其次是经过研究发现，当分类器数量过大时，反而会由于分类器间差异度的减小而降低识别率[1]。因此分类器的选择成为集成学习的重要研究方向之一，即从大量的分类器集合中挑选出具有一定差异度与准确率的分类器参与集成。

通常研究人员认为集成若干完全一致的分类器是无意义的，所选择的分类器需要具有一定的差异性、独立性与互补性[2]。目前比较流行的集成学习算法Bagging采用Bootstrap方法扰动训练集，导致生成的分类器集合具有一定的差异。而另一种适用较为广泛的集成学习算法Adaboost则采用一种权重分配机制串行生成具有一定差异度的分类器集合。诸多理论与实验证明集成算法相较于单分类器能够体现出更优的分类性能，这是由于基分类器的差异导致在目标判别时可进行互补，进而提升识别率[3]。然而缺点是随着分类器数量的增多，Adaboost会产生更大的时间开销，而Bagging则会产生部分冗余的分类器导致不必要的空间开销。因此一些学者开始进行基于差异性度量的分类器选择研究，即在保障分类精度的基础上去除冗余分类器，节约存储空间。目前基于差异性度量的分类器选择研究主要有两个方向：

（1）以一种成对差异性度量方法作为标准的分类器选择，如Li等人[4]提出的DREP（diversity regularized ensemble pruning）算法是根据分类器两两之间的差异度进行排序后选择差异度较大的若干个分类器参与集成。该方法虽然在一些数据集上得到了证明并且有效地降低了集成规模，但是仍有一些不足的地方：首先是仅考虑一种差异性度量方法，并且该方法的选择会影响排序结果；其次是排序时起始分类器的选择问题，不同的起始分类器会产生不同的排序；最后是该算法需要人为指定选择分类器的个数。

（2）以一类的差异性度量方法作为选择标准，如Cavalcanti等人[5]提出的DivP方法是将5种成对差异性度量方法加权组合后作为分类器选择标准，依据该标准将分类器集合分为若干组，并从中选择准确率最高的一组参与集成。该算法虽然有效度量了分类器的差异度，但是仍然局限于一类的差异性度量方法，并且将分类器分组后仅以准确率作为各组分类器的筛选标准，并未考虑各组的整体差异度，因此可能会导致所选择的分类器集合并不是最佳的一组。

针对以上问题，本文将成对与非成对差异性度量方法结合考虑，提出一种新的分类器选择方法。本文方法主要由两部分组成：（1）基于成对差异性度量的分类器分组。首先基于成对差异性度量公式计算得差异度矩阵，将差异度矩阵以一定方式转换为邻接矩阵后通过图的形式表示分类器的关系，即将分类器分组问题转换为图着色问题，然后运用基于遗传算法的图着色方法将图的顶点（分类器）进行动态着色分组。（2）以5种非成对差异性度量方法作为评价指标，建立基于信息熵[6]的评价体系。计算各组分类器集合的权值，并选择最佳的一组分类器集合参与最终的集成。通过实验分析本文方法与差异性度量、分类器规模的关系，并与目前流行的分类器集成方法进行对比。

本文组织结构如下：第2章介绍成对差异性度量的相关知识，并给出一种基于遗传算法的分类器分组方法；第3章建立一个基于信息熵的评价体系；第4章进行算法的收敛性分析；第5章给出实验结果与性能分析；第6章总结全文并展望未来的工作。

2 基于成对差异度的分类器分组

2.1 成对差异性度量

本文采用同质类型的（homogeneous）[7]基分类器，基于Bagging技术，通过Bootstrap方法扰动训练集，生成规模为L的分类器集合。为了度量L个分类器间的差异性采用成对差异性度量方法，并通过整体取均值得到分类器集合的差异度。

目前常用的成对差异性度量方法有Q统计法（Q-statistic）、相关系数法（correlation coefficient）、双错法（double-fault）、不一致度量（disagreement）等[8]。

（1）Q统计法

（2）相关系数法

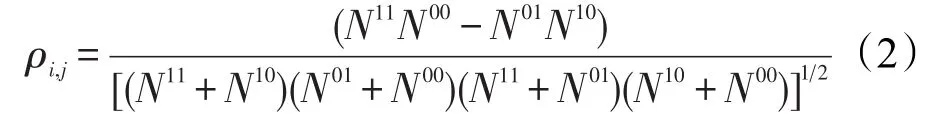
（3）双错法

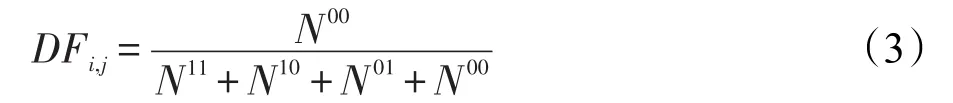
（4）不一致度量

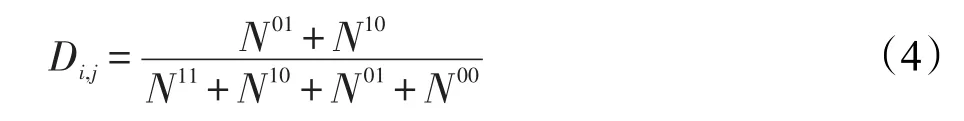
其中，Nij表示第i个分类器与第j个分类器的共同分类结果；N11与N00表示分类器ij均分类正确或错误；N10表示分类器i正确，分类器j错误；N01表示分类器i错误，分类器j正确。

结合成对差异性度量公式进行基分类器两两之间的差异度计算，生成L×L的成对差异度矩阵，如式（5）所示：

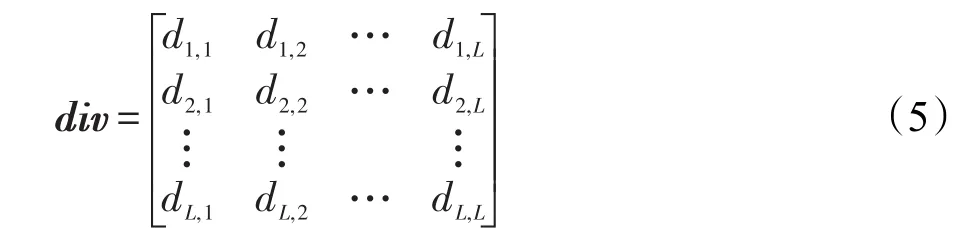
其中，div是对称矩阵，主对角线di,j(i=j)表示分类器与自身的差异度，由于分类器与自身的差异度最小，因此在计算分类器集合整体差异度时并不将此考虑在内。

2.2 差异度矩阵的转换

本文方法给出的差异度矩阵的转换方式分两步进行，其中转换阈值设置为集合的整体差异度：

（1）根据L个分类器的差异度矩阵div，计算得L个分类器集合的整体差异度为：

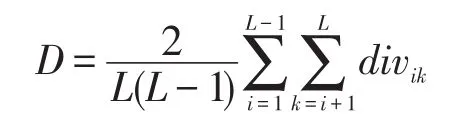
（2）根据整体差异度D，构造一个L×L的邻接矩阵H，其中：

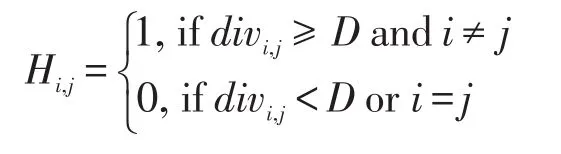
以6个分类器为例，假设式（6）为根据Q统计法计算得到的6个分类器集合的成对差异度矩阵，差异度的范围是[0,1]，差异度值越接近0代表差异度越大。通过计算得到该集合整体差异度为D=0.5。

将该成对差异度矩阵转换为邻接矩阵后如式（7）所示，需要注意的是主对角线元素为0，因为分类器自身不能与自身相连接。

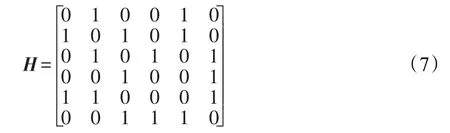
根据该邻接矩阵H可以画出如图1所示的无向图G。

Fig.1 Undirected graph G created from adjacency matrix图1 邻接矩阵转换为无向图G

图1中圆圈内标号表示1～6号分类器，由此将分类器以无向图中的一个节点表示，通过边连接的分类器差异度较小。为了尽可能多地选择出差异度较大的分类器集合，并比较其各自的集成性能，引入了图论中的着色算法。

2.3 遗传算法求解图的着色问题

图的着色问题（graph coloring problem，GCP）[9-10]是图论研究中的经典问题之一。图G=(V,E)的一个v顶点着色是指用v种颜色对图G进行着色的一种分配方案，若该方案使相邻顶点颜色不同，则称着色正常，满足此方案的最小颜色数称为图G的色数。如图2所示，即为图1中无向图G的一种着色方案，该无向图的色数为3。

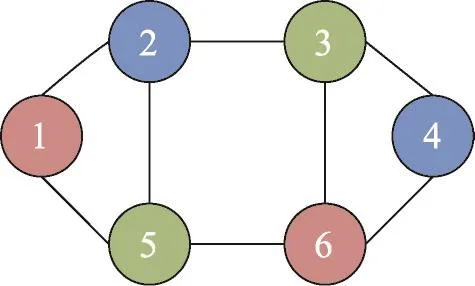
Fig.2 One coloring scheme for graph G图2 图G的一种着色方案

但是显然图2并不是唯一的着色方案，假设依旧以 Red、Blue、Green 3种颜色进行着色，Red（1,3）、Blue（2,6）、Green（4,5）同样也满足着色条件，即分类器1、3一组着红色，分类器2、6一组着蓝色，分类器4、5一组着绿色。为了得到满足要求的不同的着色方案（即得到不同的分类器分组方式），本文基于遗传算法给出了解决方式，之所以选择遗传算法是由于该算法具有良好的鲁棒性、并行性，并且随着该算法理论的不断完善，利用遗传算法解决图着色问题是当前的一个热点[11-12]。

假设集合中的分类器个数为L，每个分类器代表无向图G的一个顶点，对于每种着色方案x，对应一条染色体x1,x2,…,xL，其中xi(xi=1,2,…,k)代表所着的颜色，k为最小的着色个数。

2.3.1 适应度函数

由于k种颜色且长度为L的染色体子空间规模为kL，当集合中分类器个数较多时会使得算法效率较低，因此本文将随机产生染色体的编码方案。根据图G中节点的排列给出一种着色方案，并更新节点排序，更新规则是同颜色的节点按颜色编号依次排列。更新后序列的着色数小于等于原序列，从而找到该节点序列中的局部极小的次优解。最终根据遗传算法在次优解空间中寻找最优解。

本文方法不指定颜色数k，希望分类器集合动态分组，即自适应地找到最小颜色数k。若k种颜色下有M种着色方案，则将分类器分为kM组。因此适应度函数的设计为：

其中，wi为每个节点的权值，没有特殊情况均设为是着色序列的最大颜色数，采用该适应度函数得出的就是无向图G的颜色数k。

2.3.2 交叉算子

本文交叉算子采用部分匹配交叉法[13]，假设染色体x=(x1,x2,…,xL)与y=(y1,y2,…,yL)是参与杂交的父代个体。随机产生交叉区域[m,n]，使其变成x=(x1…ym…yn…xL)与y=(y1…xm…xn…yL)。然后确定xm～xn与ym～yn之间的映射关系xm→xm′,xm→xn′,ym→ym′,yn→yn′。利用映射得到新的合法染色体x=(x1′…ym…yn…xL′)与y=(y1′…xm…xn…yL′)，即包括图中所有顶点且不重复。如父代染色体（1,2,3,4,5,6）与（5,3,6,1,2,4）的交叉过程如图3所示。

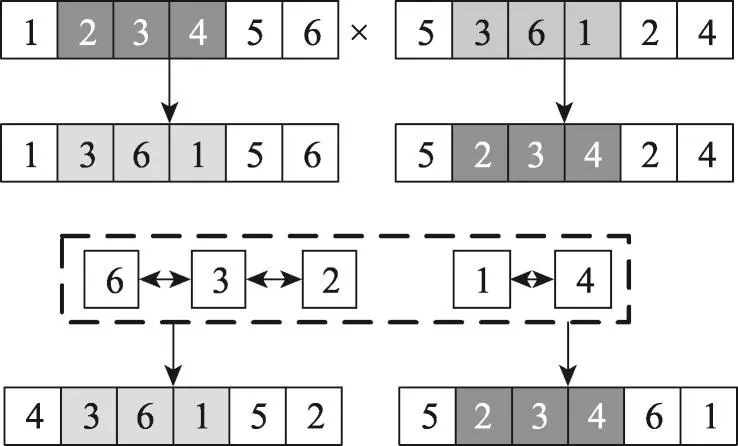
Fig.3 Process of chromosome crossing图3 染色体交叉流程

2.3.3 变异算子

x=(x1…xm…xn…xL)以等概率随机选取两个基因位m和n，然后交换该位置的基因值，交换后的染色体记为x′=(x1…xn…xm…xL)。如染色体（1,2,4,3,5,6）选取两个变异位2和5，变异结果为（1,5,4,3,2,6）。

通过该手段避免算法陷入局部最优解，并且这种换位变异执行简单，有利于种群多样性。

3 基于信息熵的分类器选择

根据着色结果得到了不同的分类器分组方式，为了从中选出最佳的一组作为最终参与集成的分类器集合，针对基分类器子集建立了一个基于信息熵的评价体系，并将非成对差异性度量作为本次评价的重要指标。

常用的非成对差异性度量方法有KW方差(M1)、Kappa度量(M2)、熵度量(M3)、难度度量(M4)、广义多样性度量(M5)[14]。将其作为评价的5项指标，分别针对不同子集进行度量计算，并建立一个非成对度量矩阵Ndiv。基分类器子集w1,w2,…,wk的非成对度量矩阵如式（8）所示。

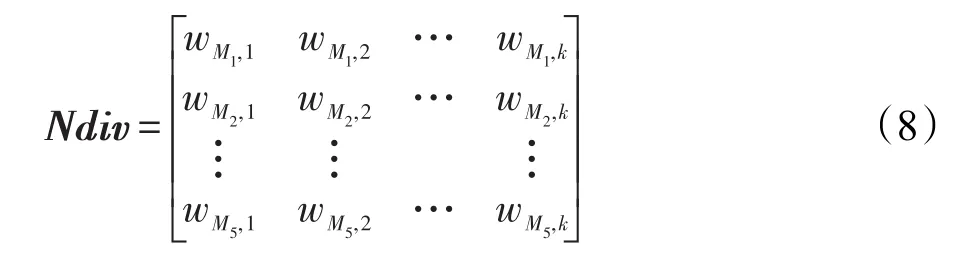
由于不同差异性度量方法的计算不同并且正负值的含义不同，因此接下来要对该矩阵进行标准化处理，即Ndiv=|Ndiv|，将差异性度量计算的绝对值转换为相对值。并对正负指标分别进行标准化处理：

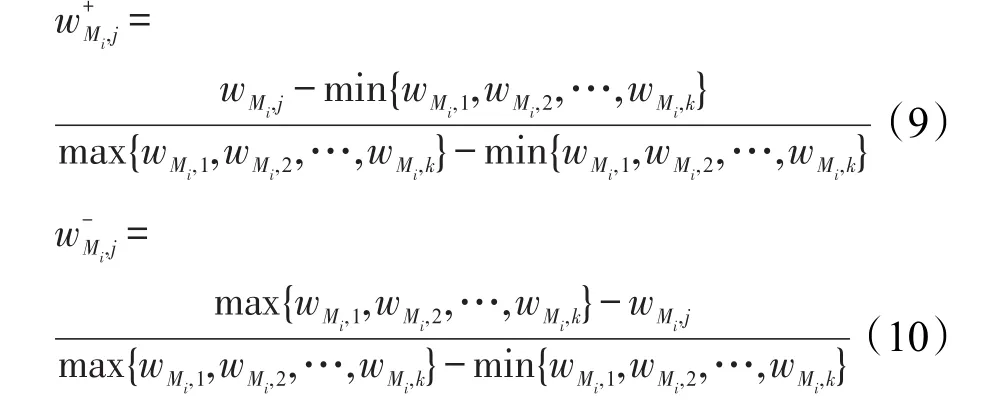
然后根据标准化后的差异度矩阵，计算各指标下第j个子集所占的比重：

其中，i=1,2,…,5，j=1,2,…,k。

接下来计算各非成对差异性度量方法的熵值：

其中λ=1/ln(k)＞0，满足

最终根据权重计算各分类器子集的综合得分：

根据最终评分选出最佳的一组分类器子集作为最终的集成对象。

4 算法收敛性分析

由于本文方法是基于遗传算法的着色分组，因此需要进行收敛性分析。

定义1若任意两个个体x和y，并且其关系为P{M∘C(x)=y}＞0，其中M∘C(x)表示染色体x经过交叉和变异产生的个体，则称x和y是可达的。

引理1当遗传算法的可行域中任意两个个体是相互可达时，且种群序列P(0),P(1),…,P(t)单调，则遗传算法以概率1收敛到全局最优解。

证明假设染色体x参与杂交的概率Pa，染色体a是x杂交变异产生的任一后代，b是a局部搜索得到的新后代，b被选上参与变异的概率为Pc。

则由x杂交变异得到y的概率为P{M∘C(x)=是从xi产生yi的概率，因此得到y由x变异可达，因此该算法是收敛的。 □

5 实验

5.1 实验方法与数据

本次实验从UCI数据库中选取了样本数范围为32～6 435的8组数据集，如表1所示。分类器的学习算法选用了不稳定的决策树（decision tree）15]，该算法会由于训练集的微小变化而改变。然后基于Bagging技术扰动训练集生成50～150个分类器集合。并且实验采用5重交叉验证，以3∶1∶1的比例分为训练集、验证集和测试集，验证集的存在是为了分析基于信息熵的评价体系。最后本次所选用的集成规则为投票法，其主要原因是这一规则无需训练，并且也是目前多数文献研究中所采用的方法[16]。

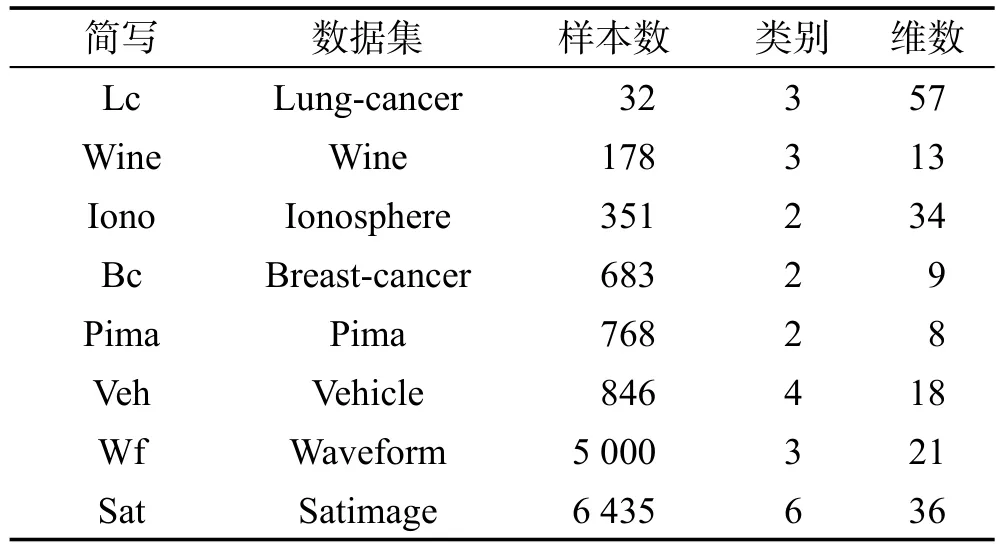
Table 1 Experimental data information表1 实验数据信息

本次实验平台为Matlab R2014a，所用的基分类器均来自PRTools（http://www.prtools.org）工具箱。

5.2 实验结果与分析

本次实验结合控制变量法分4步进行。首先分别分析影响集成效果的因素，然后给出合理化建议，最后与当前流行的集成方法进行对比。

5.2.1 分析成对差异性度量方法

当使用不同成对差异性度量方法时得到不同的差异度矩阵，因此转换的邻接矩阵有所区别，再利用遗传算法进行图着色时可能会得到不同的结果。

本次实验以目前流行的4种成对差异性度量方法(Q统计法、相关系数法、双错法、不一致度量)为标准，结果如表2所示，准确率最高的数值用加粗标记。

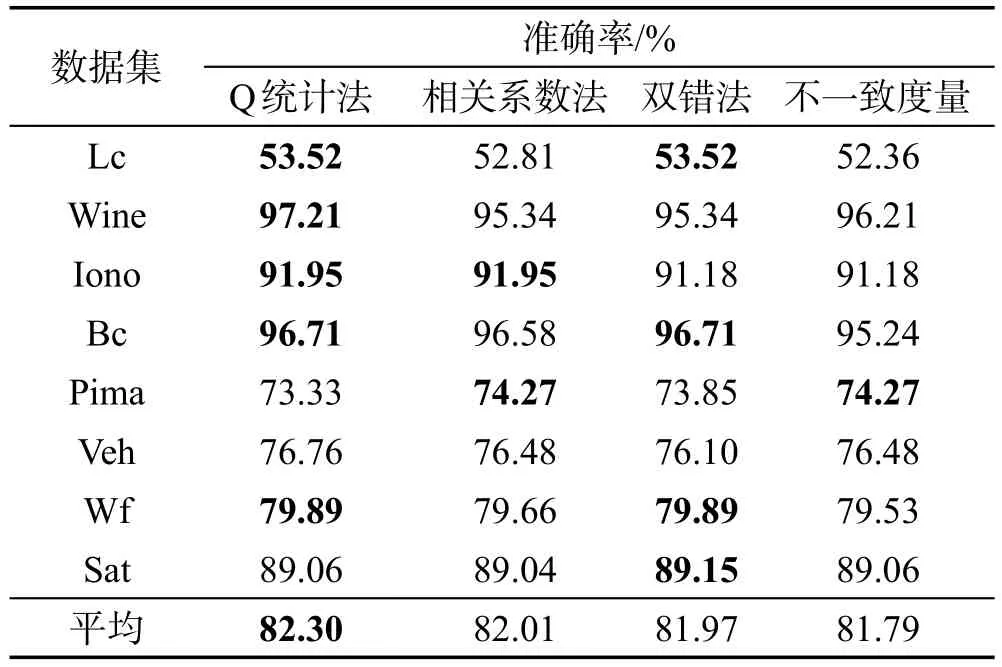
Table 2 Ensemble results of different diversity measures表2 不同差异性度量方法的集成结果

本次实验的参数：初始基分类器规模为100。

从表2可以看出，本文方法虽然在不同差异性度量标准下均可以获得较好的分类效果，但是在大多数数据集下，以Q统计法作为度量标准时可以获得相对更好的集成准确率。其次是双错法、相关系数法与不一致度量。

为了更好地比较这几种度量方法，分别计算不同度量方法选择出的分类器个数，以10次实验的平均值为最终结果，如图4所示。

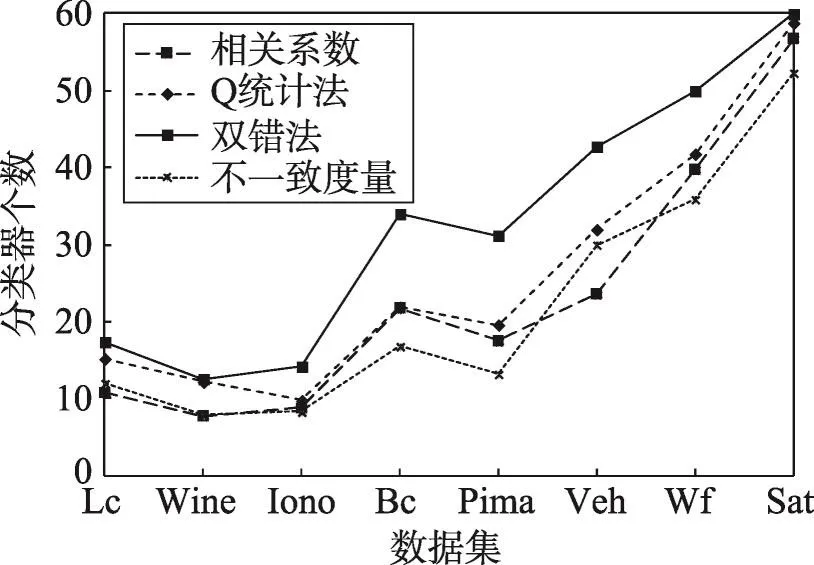
Fig.4 Number of classifiers in different datasets图4 数据集的分类器个数

由图4可以看出，无论使用哪种差异性度量方法，选择出分类器的个数都随着数据集样本数的增加而增加。通过纵向对比可以看出，这4种度量方法中双错法相较于其他方法选择出的分类器个数较多，其次是Q统计法、相关系数法、不一致度量。结合表2的集成准确率可以看出，Q统计法能在保障集成精度的同时，尽可能地相对减小集成规模，因此可以优先以Q统计法作为成对差异性度量标准。

5.2.2 分析集成规模与结果

分类器的规模是影响集成效果的因素之一。为了分析当分类器规模发生变化时，本文方法对集成结果产生的影响，本次实验首先基于Bagging生成了3种规模（50,100,150）大小的基分类器集合，并使用本文方法进行选择性集成，将最终集成结果与Bagging（Bag）直接集成进行对比，如表3所示。

本次实验参数：成对差异性度量方法为Q统计法。

由表3可以看出，当分类器规模为50、100、150的情况下，在8组数据集中本文方法相较于Bagging的集成准确率平均提升1.57%、1.98%、1.62%，其中分类器规模为100时的提升效果最高。

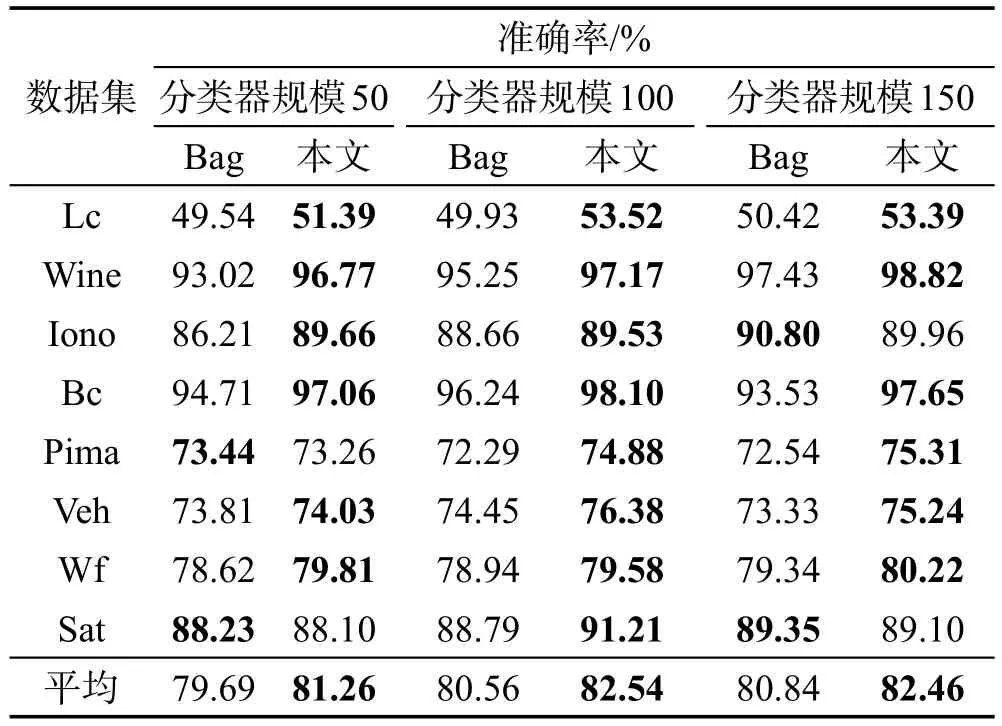
Table 3 Ensemble results on different scales表3 不同规模时的集成结果

5.2.3 分析基于信息熵的评价体系

本文提出的基于信息熵的评价体系是将5种非成对差异性度量方法动态加权，计算各组分类器综合得分，并根据评分情况进行挑选。为详细分析该评价体系，首先分别以每种非成对差异性度量方法为标准进行分类器集合的选择，结果如表4所示。

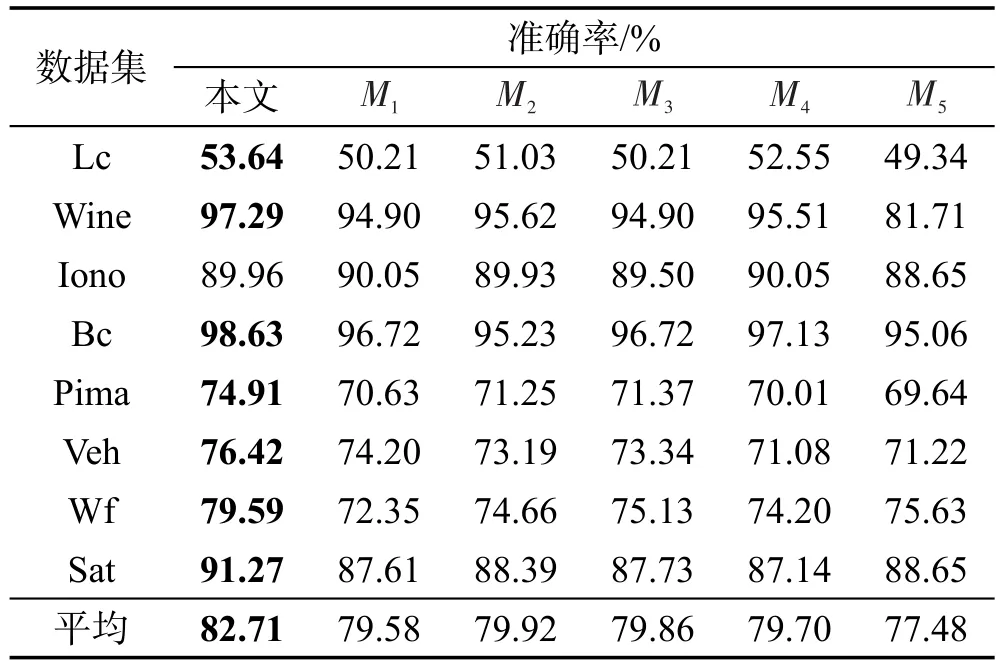
Table 4 Ensemble results of different non-pairwise diversity measures表4 不同非成对差异性度量方法的集成结果

本次实验参数：集成规模为100，成对差异性度量方法为Q统计法。

由表4可以看出，除Ionosphere数据集，由本文方法所选出的分类器集合的集成效果均好于以单个非成对差异性度量方法为标准进行挑选的分类器集合。

但是目前仅是从分类器差异性的角度进行考虑，接下来要从准确率的角度进行实验。首先将着色分组后的各集合分别对验证集进行识别，将准确率最高的一组分类器集合与通过评价体系选出的分类器集合针对测试集进行识别。实验结果如图5所示。

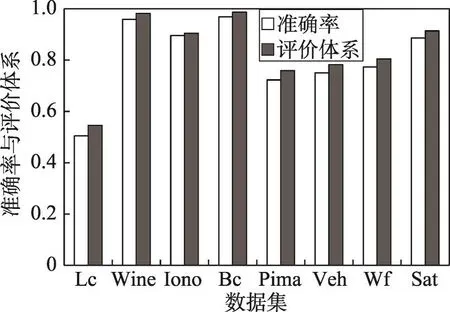
Fig.5 Accuracy and evaluation system图5 准确率与评价体系

由图5可以看出，两种分类器集合的选择方法均拥有较高的识别精度，这是由于本文方法中的基于遗传算法的着色分组合理地将差异性较大的分类器挑选出来。通过评价体系选出的集合与直接选出针对验证集准确率最高的集合在最终集成效果上非常相似，这是由于在实验过程中，两种选择方法有时选出的分类器集合是相同的。但是通过评价体系选出的分类器集成效果仍有一定的提升，因此也证明了针对验证集分类效果良好的分类器集合不一定对测试集分类效果最好。通过差异性与准确率两个角度进行的实验均证明本文提出的基于信息熵的评价体系具有一定可行性。

5.2.4 分析集成方法

上述实验中已经针对影响集成效果的因素分别进行了分析，接下来将本文方法与目前比较流行的4种集成方法Bagging（Bag）、Adaboost（Ada）、DREP[3]、DivP[4]进行比较。

本次实验的参数：集成规模为100，本文方法与DREP算法的成对差异性度量方法选择为Q统计法，DivP算法为默认参数，集成规则均为投票法。实验结果如图6所示。

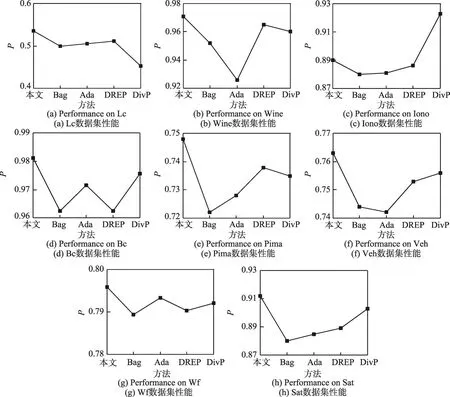
Fig.6 Performance comparison of ensemble methods图6 集成方法的性能比较

由图6可以看出，除Ionosphere数据集下本文方法的表现力略逊色于DivP算法，大多数数据集下本文方法与目前流行的集成算法相比，均接近或者超过其识别精度。本文方法与DivP算法的主要区别在于DivP算法以准确率作为各组分类器的筛选标准，而本文方法则是以准确率与差异度建立了一种评价体系作为各组分类器集合的筛选标准。事实证明大多数数据集下本文提出的方法具有一定的可行性。

6 结束语

选择出具有一定差异度的分类器集合是获得良好集成效果的前提之一。本文将成对与非成对差异性度量方法结合提出了一种新的分类器选择方法，并分析该方法以不同成对差异性度量作为标准、不同分类器规模下的集成效果，将该方法与目前流行的若干种集成方法进行对比分析，最终得到了有一定指导意义的结论。

此外本文方法有待改进的地方主要有两点：（1）分类器着色分组过程中，差异度矩阵转换邻接矩阵时的阈值设置可以进行改进，本文的阈值是采用整体差异度的平均值，后续研究也可尝试其他设置方式。（2）本文的图着色方法是基于遗传算法提出的，后续也可以尝试模拟退火或蚁群算法等启发式算法。因此拟将算法根据这两部分进行分析与改进，以提升分类器集成精度。