考虑区间元素个数的区间犹豫模糊决策方法*

阮传扬，韩莉娜

1.广东财经大学 工商管理学院，广州 510320

2.上海交通大学 安泰经济与管理学院，上海 200030

3.广东省生产力促进中心，广州 510070

1 引言

近年来，由于决策环境的不确定性以及人类认知的局限性，传统的决策方法很难适应时代潮流，已然无法解决现实中的很多决策问题，相应的模糊决策理论应运而生。自文献[1]提出能够刻画模糊现象和解决模糊问题的模糊集以来，随着时代的进步，相关学者对其进行了扩展[2-3]，目前模糊集及其扩展理论广泛应用于模式识别、智能控制、项目投资、人事评估等实际决策问题中[4]。传统的模糊集及其扩展形式因不能有效刻画犹豫信息而受到约束，文献[5-6]提出了一种能够有效反映犹豫信息的犹豫模糊集理论，其最大特点是允许一个属性同时出现不同的评估值，可以有效避免决策信息的缺失。然而，大多实际决策问题中，犹豫信息往往很难用精确的评估值来表达，因而文献[7]将区间数与犹豫模糊信息相结合提出了区间犹豫模糊集，即用多个区间数表示出现的可能隶属度。

目前有关区间犹豫模糊集的信息集成、距离测度、相关系数等已被应用到诸多领域，例如工厂选址、杰出人才评估、水库运营模式选择、云计算安全评估、应急预案评估、能源项目评估等[8-15]。距离测度是运用区间犹豫模糊信息进行多属性决策的一项关键方法，文献[16]定义了区间犹豫模糊距离公式，并在此基础上构造了区间犹豫模糊标准化公式，之后提出一种区间犹豫模糊灰色妥协关联决策方法，并将其有效应用于云计算安全评估的实例中。文献[17]将熵值引入到区间犹豫模糊集中，提出了基于熵值的区间犹豫模糊距离测度和相似度公式，并将其应用于软件评价问题中。文献[18]提出了基于区间犹豫模糊信息的汉明距离、欧氏距离以及豪斯道夫距离的具体表达式，并将其有效应用于多属性决策问题中。在上述区间犹豫模糊距离测度中，不同的区间犹豫模糊元所含区间元素个数可能存在差异，目前采用的一种方法就是在含有区间元素较少的区间犹豫模糊元中人为添加区间元素，缺点就是主观随意性过大，随着决策者风险态度的不同，备选方案排序也会随着发生变化，很难做到备选方案排序的最终统一。针对人为添加元素的问题，文献[19]首先给出了犹豫模糊集犹豫度的概念，之后在此基础上给出了符号距离的定义，有效解决了这个问题，但是该种方法未将犹豫模糊元中元素个数的影响考虑进去，在某些情况下决策结果不理想，具有一定程度的局限性。文献[20]经过深入分析，发现上述区间犹豫模糊距离测度定义中仅考虑了不同区间犹豫模糊元之间的差异，忽视了区间犹豫模糊元的个数之间的差异，这一缺陷将会直接影响实际决策问题中的决策效果。文献[21]考虑到了决策者分歧程度以及元素个数的双重影响，提出了基于犹豫模糊信息的改进犹豫度的概念，并以此为基础给出了犹豫模糊集的改进符号距离的定义，做到了一定程度的应对，但是元素个数的影响过大，甚至超过了元素本身数值及其离散程度的影响，在元素个数偏少或相差不大的情况下会导致决策结果与直观认识情况不符的现象。

鉴于此，本文首先给出一种基于区间犹豫模糊信息的改进犹豫度与改进符号距离的概念。其次，针对区间犹豫模糊元中的区间元素个数和方差构造一种区间犹豫度，基于区间犹豫度提出相应的区间符号距离，可以很好地反映决策群体的分歧程度且区别度明显。最后，给出了一种具有属性优先级的区间犹豫模糊决策方法，并将其应用于项目投资的实际决策问题中，以此验证本文所提方法的有效性和合理性。

2 基础理论

为了解决同一属性中同时出现不同区间评估值的现象，文献[7]在犹豫模糊集的基础上给出了区间犹豫模糊集的概念。

定义1[7]设X={x1,x2,…,xn}是一个非空集合，则称：

区间犹豫模糊元的运算法则如下：

定义 2[7]设为3个区间犹豫模糊元，且λ≥0，则它们之间的运算法则如下：

基于区间数的定义，文献[22]给出了区间数之间的相关运算法则如下：

定义3[22]设为一组区间数，且λ≥0，则它们之间的运算法则如下：

另外，均值以及方差如下：

犹豫模糊元中的元素反映了决策者的分歧或犹豫程度，元素之间偏差越大，犹豫程度越高。为了反映决策者的犹豫程度，文献[19]定义了犹豫模糊元的犹豫度。

定义4[19]设h={γi|i=1,2,…,lh}为一个犹豫模糊元，γi为h中第i小的元素，lh为h的元素个数，则h的犹豫度如下：

基于定义4的犹豫度，文献[19]定义了犹豫模糊符号距离，定义如下：

定义5[19]设h={γi|i=1,2,…,lh}为一个犹豫模糊元，γi为h中第i小的元素，lh为h的元素个数，采用犹豫模糊元最大值1ˉ为理想点犹豫模糊元，则由h到1ˉ的符号距离如下：

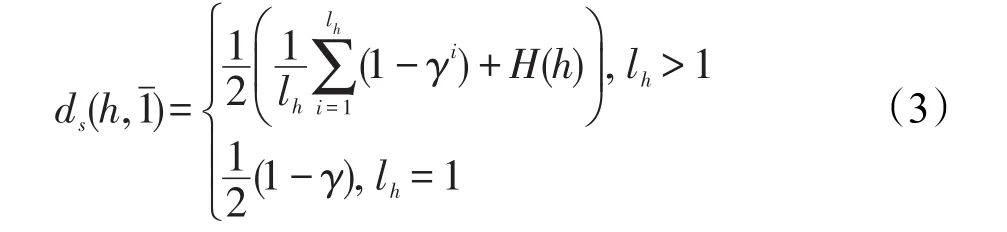
犹豫模糊信息体现的是决策者的不同意见，犹豫模糊元中在“重复决策数据仅保留一个”的情况下元素越少，表示意见越统一，为了考虑犹豫模糊元中的元素个数对决策结果的影响，文献[21]提出了一类改进的犹豫度和符号距离。

定义6[21]设h={γi|i=1,2,…,lh}为一个犹豫模糊元，γi为h中第i小的元素，lh为h的元素个数，则h的改进犹豫度如下：

定义7[21]设h={γi|i=1,2,…,lh}为一个犹豫模糊元，γi为h中第i小的元素，lh为h的元素个数，1~为理想点犹豫模糊元，则称:

为h到͂的改进符号距离。

3 基于区间犹豫模糊信息的多属性决策方法

犹豫模糊信息揭示的是决策者的不同意见，具有很大的不确定性，这种不确定性加大了决策的难度，为了有效测度这种分歧度，决策者进行决策时通常给出的是区间犹豫模糊信息，鉴于此，本文给出一种基于区间犹豫模糊信息的区间犹豫度的概念，并在此基础上给出基于区间犹豫模糊信息的区间符号距离的定义，之后将其应用于属性之间具有优先级关系的犹豫模糊决策问题中。

3.1 基于区间犹豫模糊信息的符号距离

为了对决策信息进行有效处理，距离测度近年来被有效应用于多属性决策中，文献[21]考虑到了决策者分歧程度以及元素个数的双重影响，给出了改进的犹豫度和符号距离的概念，本文基于此给出了一种基于区间犹豫模糊信息的改进犹豫度和符号距离的定义。

定义 8设为一区间犹豫模糊元，͂的区间元素个数，则͂的改进犹豫度如下：

表示区间犹豫模糊元的方差。

定义 9设为一区间犹豫模糊元，͂的区间元素个数̂为理想点犹豫模糊元，则͂的改进符号距离如下：

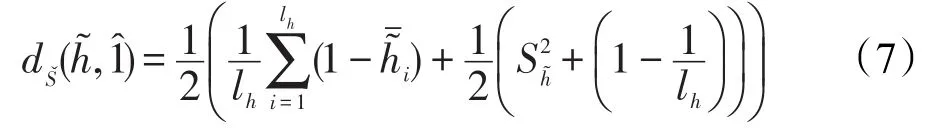
然而，定义8和定义9对元素个数的处理上并未完全到位，例如，若存在3个元素数量不等的区间犹豫模糊元改进犹豫度为改进符号距离为通 过 分 析以上结果可知：在元素个数偏少且大于1的情况下，区间犹豫模糊集中区间元素个数的影响过大，甚至超过了区间元素本身数值及其离散程度的影响，极有可能导致最终决策结果与直观认识情况不符的现象。

为解决这类问题，本文引入对数变换的概念，主要是由于对数变换是数据变换的一种常用方式，其目的在于使数据的呈现方式接近所希望的前提假设，从而可以更平滑地进行统计推断。例如：经济数据大多数都是偏态分布，比如收入GDP之类的，而且大多是右偏的，取对数后不会改变数据的性质和相关关系，但压缩了变量的尺度，从而形成正态分布的数据，这样数据更加平稳，也削弱了模型的共线性、异方差性等。因此，本文给出一种基于区间犹豫模糊信息且含有对数变换的区间犹豫度的概念，之后在此基础上给出基于区间犹豫模糊信息的区间符号距离的定义，并讨论其基本性质。

定义 10设为一区间犹豫模糊元，͂的区间元素个数，则͂的区间犹豫度如下：

表示区间犹豫模糊元的方差。

式（8）为基于区间犹豫模糊元中区间元素的方差以及个数定义的区间犹豫度，偏差越大，区间元素个数越多，所对应的区间犹豫度也越大。

区间犹豫度满足如下性质[19,21]：

性质 1设为一区间犹豫模糊元，其对应的补集为

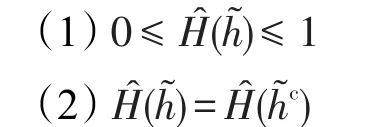
易于验证式（8）满足性质1。

证明（1）由于方差的取值范围为[0,1]，则

（2）由补集的方差：

而区间犹豫模糊元中的区间元素数量lh恒定，则恒成立。 □

基于区间犹豫模糊信息的区间犹豫度，可以得到一种相应的区间符号距离。

定义11设为一区间犹豫模糊元，͂的区间元素个数，1̂为理想点犹豫模糊元，则͂的区间符号距离如下：

区间符号距离满足如下性质[19,21]：

性质 2设为 3 个区间犹豫模糊元，1̂为理想点犹豫模糊元，则：

3.2 考虑属性优先级的属性权重确定方法

本文给出一种考虑属性优先级的混合加权方法，保证该方法既能考虑属性优先级，又能包含属性信息的离散程度。详细步骤如下[23]：

（1）决策专家组给出属性优先级信息。

（2）通过计算第j项属性的基于区间犹豫模糊信息的区间符号距离方差ej来确定相邻优先级属性xj与xj+1重要性程度之比rj。

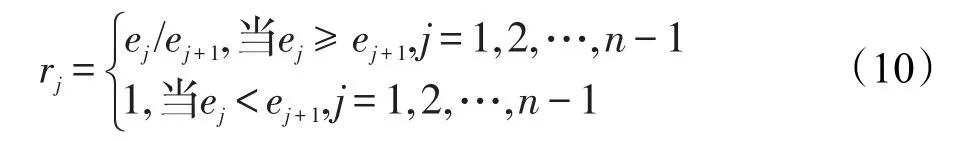
其中，令rn=1。

（3）根据给出的rj值，按照属性优先级从高到低的顺序计算优先级排序在第k个属性的权重tk为：

3.3 区间犹豫模糊多属性决策步骤

基于式（9）的区间符号距离以及式（11）属性权重确定方法，给出一种属性具有优先级关系的区间犹豫模糊多属性决策方法。假设方案集为A={A1,A2,…,Am}，属性集为G={G1,G2,…,Gn}，其对应的权重向量为专家组E={e1,e2,…,ep}中每位专家在进行匿名评价时给出每个方案Ai∈A关于每个属性Gj∈G的区间评价值，去掉完全重复的区间元素，就组成了一个区间犹豫模糊决策矩阵是一个区间犹豫模糊元。

基于区间符号距离和属性优先级的区间犹豫模糊多属性决策步骤如下：

步骤1专家组给出每个方案Ai∈A关于每个属性Gj∈G的区间评价值，得到区间犹豫模糊决策矩阵H=(hij)m×n。

步骤2首先利用式（9）计算区间符号距离，其次依据式（11）得出具有属性优先级的权重信息W=(ω1,ω2,…,ωn)T。

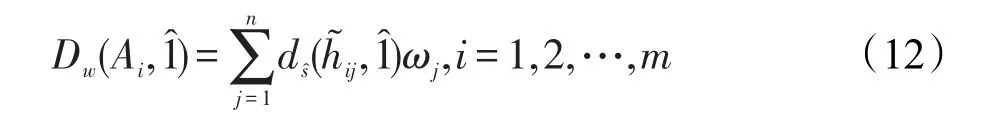
步骤3利用式（12）中的加权符号距离公式：得出各方案A={A1,A2,…,Am}的加权符号距离并根据的大小对各方案进行排序，加权符号距离̂越小，相应的方案Ai越优。

4 数值算例分析

深圳一国际投资银行准备将一笔资金用于市场投资，假设目前备选方案为：软件公司A1、旅游公司A2、食品公司A3、汽车公司A4和建筑公司A5。为了客观科学进行决策，该投资银行的领导层邀请相关专家进行决策，专家组决定在发展潜力G1、投资安全系数G2、收益率G3以及产品替代性G4这4个属性下进行综合评估，并且属性权重向量未知，但决策小组事先给出了属性优先级关系G4≻G1≻G2≻G3，专家小组给出每个方案Ai∈A关于每个属性Gj∈G的评价区间值，去掉完全重复的区间数据，就组成了一个基于区间犹豫模糊信息的决策矩阵{[0.3,0.4],[0.5,0.6]}表示第2个公司（即旅游公司）在第1个属性（即发展潜力）方面专家小组有两种不同观点，即方案A2关于属性G1的评价区间值有[0.3,0.4]和[0.5,0.6]两种。

为了获得最佳投资公司，基于区间符号距离的多属性决策步骤如下：

步骤1专家组给出每个方案Ai∈A关于每个属性Gj∈G的区间犹豫模糊决策矩阵，见表1所示。

步骤2首先利用式（9）计算区间符号距离，见表2。其次依据式（11）得出属性权重：

W=(0.305 1,0.215 9,0.173 9,0.305 1)T

步骤3利用式（12）中的加权符号距离公式得出各方案A={A1,A2,…,Am}的加权符号距离

Table 1 Interval-valued hesitant fuzzy decision making matrix表1 区间犹豫模糊决策矩阵

Table 2 Interval-valued signed distance matrix表2 区间符号距离

为了获得最佳投资公司，若采用定义9改进符号距离的话，具体多属性决策步骤如下：

步骤1′同步骤1。

步骤2′首先利用定义9计算改进符号距离，见表3。其次依据式（11）得出属性权重：

W=(0.317 8,0.182 2,0.182 2,0.317 8)T

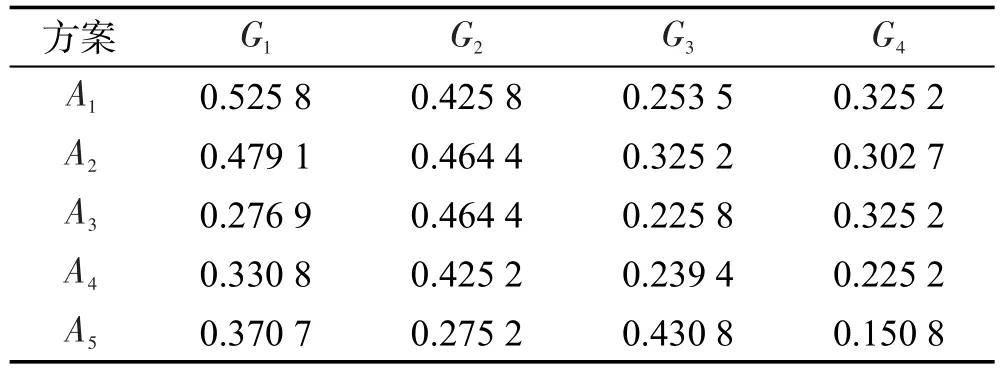
Table 3 Improved signed distance matrix表3 改进符号距离

步骤3′利用式（12）中的加权符号距离公式得出各方案A={A1,A2,…,Am}的加权符号距离

由以上结果可知，本文所述方法主要优势以及适用条件如下：

（1）采用基于区间犹豫模糊信息的区间符号距离法进行决策时不仅考虑了区间犹豫模糊元中区间元素的均值大小以及离散程度等影响，还考虑了区间犹豫模糊元素个数的影响，包含的范围比较广，所得决策结果具有较好的区分度和稳定性，有效性也更高。

（2）本文基于属性优先级和区间犹豫模糊符号距离建立的属性权重确定方法属于主客观组合赋权方法，既能保持属性优先级恒定，又能有效利用已有区间评价信息科学合理地确定出属性权重，数值案例表明该方法所得决策结果合理、可靠。

（3）由数值案例可知，在区间犹豫模糊决策矩阵中区间元素较少的情况下，区间符号距离适用范围比较广，所得决策结果合理、有效。不过，当决策矩阵中区间犹豫模糊集中区间元素较多时，由于定义11中有关区间犹豫模糊元素个数的计算公式部分随着区间元素个数的增大而趋向于1，则区间元素个数对决策结果的影响不大且计算复杂度较高。因此，这种情况下采用文献[17-19]等经典算法比较合适。

5 结束语

本文基于区间犹豫模糊元中区间元素的方差与个数提出了一类区间犹豫模糊符号距离，并在此基础上研究了属性具有优先级关系的多属性决策问题。主要工作如下：

（1）为了考虑元素个数的影响，利用文献[21]中基于犹豫模糊信息的改进犹豫度和改进符号距离，给出了基于区间犹豫模糊信息的改进犹豫度和改进符号距离的定义。

（2）基于区间犹豫模糊元中区间元素的方差与个数定义了一种含有对数函数的区间犹豫度，以便合理反映决策者的分歧程度。

（3）基于区间犹豫度定义了一种同时考虑区间犹豫模糊元中区间元素大小、数量和方差的区间犹豫模糊符号距离，通过数值案例可知区间犹豫模糊符号距离具有区分度明显，决策结果更加合理、可靠的特点。

（4）针对属性具有优先级的多属性决策问题，本文基于区间犹豫模糊符号距离和属性优先级提出了一种属性权重确定方法，之后利用加权符号距离对备选方案进行排序。

采用本文方法进行决策时同时考虑了区间犹豫模糊元中区间元素的大小、数量、离散程度等多重影响，因而决策结果具有较好的区分度和稳定性。