让数学核心素养在教学中落地生根——以《用坐标表示平移》一课为例

吉林省延边地区延吉市第十三中学 金香丹

数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六个方面。数学学科核心素养的培养，要通过学科教学和综合实践活动课程来具体实施，数学学科教学活动是数学学科素养培养的主要途径。下面我就以《用坐标表示平移》教学中体现数学核心素养的方法谈一谈自己的体会。

一、教学片段检录及评析

情境再现一：这堂课第一个环节：导入部分采用了类比导入法

一辆车在数轴上跑（如图1），车从数轴上的A点(表示的数为-1)出发。求：（1）向右平移3个单位长度后表示的数；（2）向右平移a个单位长度后表示的数；（3）向左平移4个单位长度后表示的数；（4）向左平移a个单位长度后表示的数。

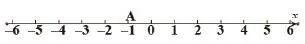
图1

评析：这里（1）（3）题用多媒体展示很直观地就求出来了，但是（2）（4）题就很抽象了，这就体现了数学核心素养的数学抽象，学生可以从-1+3=2和-1-4=-5的感性认识升华到-1+a和-1-a的理性认识。这就说明一个点在数轴上平移时，向右平移加平移距离，向左平移减平移距离的规律，这为下一步学生们自行得出平面直角坐标系内点的平移规律做了一个铺垫，并且渗透了类比思想。这也是学生们的数学思维从一维到二维的转变，即从简单的左右平移到平面直角坐标系内上下左右的平移。

情境再现二：这堂课第二个环节：探究坐标平面内点的平移和坐标变化规律

导学案第一个活动设置了一个探究栏目（如图2）：探究：将点A（-2,-3）向右平移5个单位长度，得到点A1,在图上标出这个点，并写出它的坐标。把点A 向左平移4个单位长度，向上平移5个单位长度，向下2个单位长度之后的点分别在图中标出来，并写出它的坐标。观察坐标的变化，你能从中发现什么规律吗？

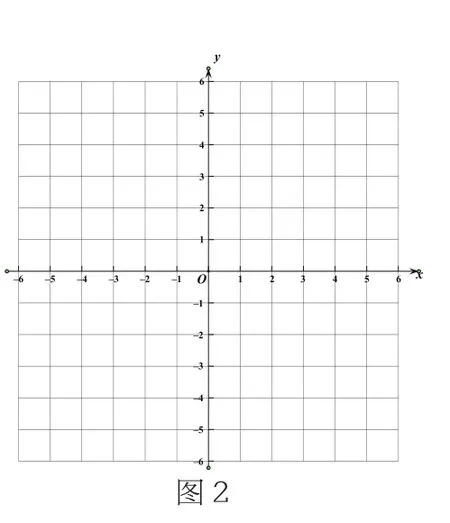
评析：在这里我让学生先独立思考，然后通过小组讨论得出坐标变化规律。此过程中，在坐标系中找出点并写出坐标，学生就很直观地得出了答案。但是得出变化规律就很抽象，也是这节课的难点了。之所以难，不仅觉得抽象，而且还要分类，即左右平移和上下平移的分类，横坐标与纵坐标的分类。在做题中学生经常出现错误的原因之一就是考虑不全面，这就说明分类思想在解决问题中的重要性。所以，教学中尽可能地给学生渗透这些数学思想，通过学生充分的讨论还有导入部分的总结规律就很顺利地总结出点在平面直角坐标系中的变化规律了，从而达到了分散难点的目的。在这个过程中渗透了数形结合思想和分类思想，并培养了学生的概括能力。

情境再现三：验证环节

学生先按着刚才得出的规律，自己试着写出点（1,2）进行左右上下平移后的坐标，此过程有助于学生进一步熟悉坐标变化规律，然后在平面直角坐标系中找出点并和刚才写出的坐标进行比较，从而达到了验证的目的。

接着给出这样的题：（1）求出点（1,2）左右平移a个单位长度和上下平移b个单位长度之后的点的坐标；（2）求出点（x,y）左右平移a个单位长度和上下平移b个单位长度之后的点的坐标。（如图3）

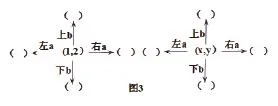
图3

评析：这个过程跟导入部分用-1+a和-1-a来归纳平移当中数的变化规律很相似，差别在于数学思维从一维到二维的转变。用字母概括规律是归纳问题当中发现规律很有效的方法，而且体现了类比思想，用类比思想解决问题是近几年中考的热点问题，所以，教学中尽可能地渗透这些数学思想是很有必要的。这个过程从数和数转化成数和字母、字母和字母，体现由易到难，分散难点，概括规律很顺利。这个过程也是从直观到数学抽象的，还体现了数学建模思想，从而落实了这堂课的重点——理解平移与坐标变化的关系。

情境再现四：出练习题，进一步巩固点的平移与坐标变化规律

评析：练习题的安排循序渐进，按照数和数数和字母以及点的两次平移的顺序来安排，既符合学生的认知规律，又体现了因材施教。

二、教学思考

从平常的初中教学中我们可以发现，很多学生上课能听懂，但是遇到问题自己却解决不了。这种情况的出现就是因为学生没有能够把握住本质，其思维还没有发散开来。这堂课提倡思维的探究性、渐进性，所体现出的数学思想和数学素养有助于进一步发展学生的数学思维，不仅有效完成了这堂课的教学目的，而且更有利于提高学生解决问题的能力和创新能力，这对于学生的长远发展来说是非常有益的。