微运动柔性并联平台的仿真分析与设计*

高兆康, 候富龙

(1.中南大学 机电工程学院, 湖南 长沙 410083; 2.中南大学 高性能复杂制造国家重点实验室, 湖南 长沙 410083)

0 引 言

相对于传统运动副,柔性铰链具有无摩擦、无间隙、高精度等特点[1]。由于在光电子封装[2]中空间较小,因此,需要在满足柔性并联平台行程的条件下,实现平台结构的最优化。柔性铰链的变形对平台行程有重要的影响,为了满足平台性能的要求,柔性铰链的材料选择为铍青铜[3],外形选择为哑铃状[4]。由于六轴并联平台的刚性高,在光电子封装中受力较小,因此,本文忽略支链结构对平台刚度的影响,主要分析支链结构对平台行程的影响。

国内外关于柔性并联平台行程计算主要是依靠其运动学的计算[5]。董为通过对平台的铰链、连杆进行建模,并利用神经网络的方法进行迭代得到运动模型,计算精确,但前期的结构设计过于复杂[6,7]。矫杰利用MATLAB建模仿真得到平台的行程,用刚性球铰代替柔性铰链,忽略了柔性铰链在运动中的变形,会产生近20 %的误差[8]。

上述研究中,大部分未考虑支链角度与平台行程的对应关系。为此本文提出了一种联合仿真的方法,通过在ADAMS软件中施加力,得到各支链协调运动数据,并将数据导入ANSYS软件中,判断运动过程中柔性铰链的应力是否达到极限,以获得平台的最大行程。并通过此方法,在建模仿真中改变支链的角度,实现结构最优化。

1 柔性并联平台行程分析

1.1 柔性并联平台结构

设计的六自由度柔性并联平台结构如图1所示。

图1 柔性并联平台的结构示意

平台有6个支链,每个支链由上下2个柔性铰链和中间的连杆组成,底部有6个电机通过导轨分别与柔性铰链相连,其中电机3,6位于y轴方向上,电机1,2,4,5平行于x轴。电机只直线运动,拟选用的电机为Nanomotion公司的HR4系列压电陶瓷电机,最大的连续推力为16 N。柔性并联平台的结构参数和材料如表1所示。

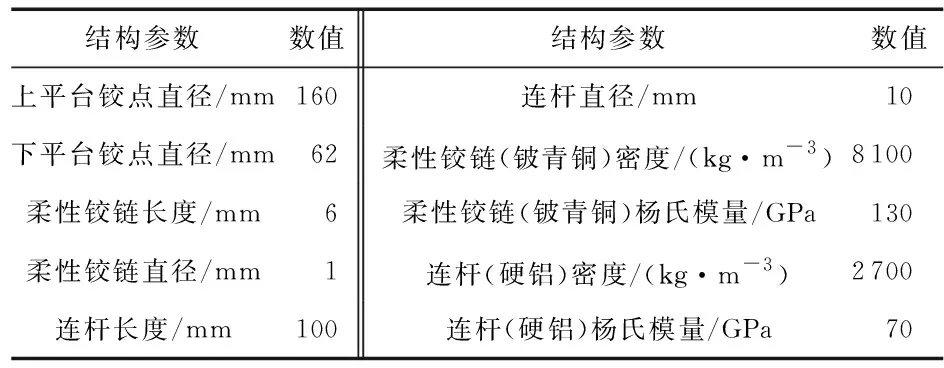
表1 柔性并联平台结构参数

1.2 柔性并联平台的动力学仿真

参考对Stewart并联机器人的控制[9],对平台模型中支链3,6的电机均施加水平y轴方向16 N力,时间为0.002 s,其余的电机不施加力,可以在x轴方向自由运动。通过ADAMS仿真,可以得到各个电机在0.002 s内的运动情况,如图2所示。

图2 并联平台各电机协调运动位移

1.3 柔性并联平台的力学仿真

在ADAMS中施加电机最大推力,将平台的运动数据导入到ANSYS中,获得铰链的最大应力σmax,通过判断柔性铰链所受应力是否达到铍青铜的屈服强度σs(1 035 MPa),得到动平台的最大行程:若σmax>σs,代入下一时刻数据；否则,取上一时刻位移为最大行程。

在ANSYS仿真中,柔性铰链的应力随着时间的增大而增大。在1.080 ms时,应力接近最大值1 034.9 MPa,动平台在y轴方向达到的最大行程为0.725 7 mm,各个电机的运动情况如表2所示。

表2 1.080 ms时各个电机的位移 mm

同理,对支链1,2,4,5的滑块施加水平平行于x轴的16 N的力,电机3,6不施加力,时间为0.002 s。按照上述步骤,得到动平台在x轴方向的最大行程为0.791 0 mm。

2 支链夹角对动平台行程的影响分析

支链的角度对并联机器人工作空间有较大的影响,本文通过改变支链夹角来验证其与动平台行程的关系,由于支链夹角不易测量,采用与其正相关的支链在定平台投影的夹角α代替,如图3所示。为了避免装配时电机、光栅尺的干涉,只对支链投影夹角分别取40°,45°,50°,55°,60°进行建模[10]。

将ADAMS中得到的10个电机协调运动的数据导入ANSYS中进行力学分析,判断在柔性铰链的弹性允许的范围内的y轴方向的最大行程,同理得到x轴方向,其结果如图4所示。动平台的最大行程随着角度的增大而减小,电机1,2,4,5的位移绝对值随着角度的增大而增大,电机3,6的位移绝对值随着角度的增大而减小。相对于y轴方向,角度的变化对x轴方向的最大行程影响很小。综合考虑平台模型支链投影夹角选择为40°。

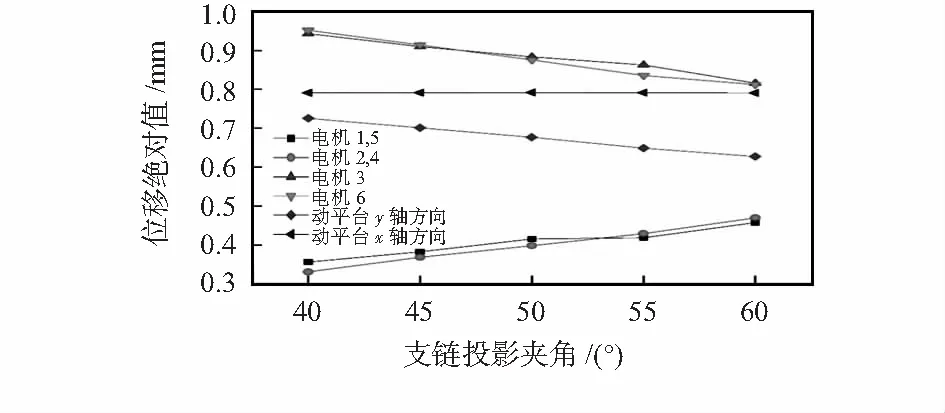
图4 支链投影夹角与最大行程的关系

3 支链与定平台夹角对动平台位移的影响分析

类似地,通过改变支链与定平台的夹角,进行建模仿真分析得到动平台行程与其夹度的关系。为了避免电机装配的干涉和并联平台的尺寸过大,只对夹角分别取50°,55°,60°,65°,70°进行建模[8],支链与定平台的夹角β如图3所示。

通过仿真分析可知动平台在y轴的方向的最大行程随角度的增大而减小,x轴方向的行程相对变化很小,如图5所示,综合考虑平台模型支链与定平台的夹角选择为50°。

图5 支链与定平台的夹角与最大行程的关系

4 结 论

针对柔性并联平台的行程分析,本文提出了一种ADAMS和ANSYS联合仿真的方法,充分考虑了柔性铰链变形对行程的影响。并通过分别改变支链之间夹角和支链与定平台的夹角进行建模仿真分析,得到支链角度与平台行程的关系。当支链投影夹角为40°,支链与定平台夹角为50°时,柔性并联平台的结构为最优化。