基于平行螺旋传输线的拉伸形变传感器研究*
王茂杰, 童仁园, 李 青
(中国计量大学 机电工程学院,浙江 杭州 310018)
0 引 言
位移形变量是地质灾害实时监测中重要的物理量之一。位移形变量的监测主要使用的传感技术有:全球定位系统(global positioning system,GPS)定位技术[1]、全站仪[2]、拉绳式位移传感器、基于同轴电缆的形变传感器[3]、基于光纤的形变传感器[4,5]和基于平行螺旋传输线的拉伸形变传感器。其中,基于平行螺旋传输线的形变传感器可实现较大拉伸形变的连续分布式测量,但目前精度较低,对平行螺旋传输线特性阻抗与拉伸形变量之间关系的理论分析存在较大误差。因此,为了能够更加准确地对拉伸形变进行分布式测量,有必要从电磁场原理及有限元仿真的角度,对特性阻抗与拉伸形变量的关系进行进一步研究。
1 平行螺旋传输线结构和测量原理
平行螺旋传输线的结构如图1所示,主要由中心硅胶条、硅胶外皮的平行铜导线和外层硅胶保护套组成[6]。

图1 平行螺旋传输线结构示意
特性阻抗是表征平行螺旋传输线典型特性的参数,对于无损耗传输线(R=0,G=0)或低损耗传输线(R≪jωL,G≪jωC),特性阻抗Z可以进一步简化为分布电容与分布电感的关系[7]
(1)
式中R为单位长度的电阻值,Ω/m;L为单位长度的电感量,H/m;G为单位长度的电导,S/m;C为单位长度的电容值,F/m。
时域反射法(time domain reflectometry,TDR)是一种基于电磁波时域反射原理的测试技术[8],其在平行螺旋传输线的一端施加一个阶跃信号,并采集反射的电压信号,通过反射系数计算出每一点的特性阻抗。特性阻抗变化的位置就是平行螺旋传输线发生形变的位置,特性阻抗变化的大小反映了形变量的大小,即根据平行螺旋传输线的特性阻抗来实现形变分布式测量。
2 平行螺旋传输线特性阻抗的有限元仿真分析
2.1 分布电感分析
使用Maxwell16软件创建3D仿真设计,选择求解类型为静磁场,绘制出平行螺旋传输线的模型如图2(a)所示,图2(b)为拉伸形变后的平行螺旋传输线模型,考虑计算机性能及速度,选择仿真圈数为3。平行导线材料配置为铜,半径0.5 mm,平行导线之间的距离为1.6 mm,螺旋导程初始值为3.2 mm,包裹材质为硅胶,相对磁导率为1。创建包含整个几何体的仿真域,将平行导线末端短路,配置电流激励为0.02 A,类型为标准型,即不考虑趋肤效应,设置收敛条件后进行设计检查,确认无误后开始分析求解,求解需要一定时间,完成后查看平行螺旋传输线的电感仿真结果。

图2 平行螺旋传输线模型
由于平行导线的长度不变,当平行螺旋传输线被拉伸时,导程值变大,螺旋半径减小,计算得螺旋半径、拉伸量与导程的关系如表1所示。

表1 螺旋半径、拉伸量与导程的关系(圈数为3)
导程值越大代表拉伸形变量越大,修改导程值和螺旋半径,仿真得到的电感量变化曲线如图3所示,由于两导线不满足密绕的条件,导线之间存在漏磁,因此电感量不为0 pH,且随着拉伸量的变大,漏磁增加,电感量会随之变大。
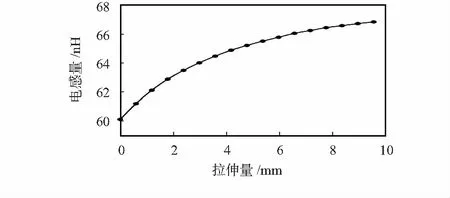
图3 分布电感量随拉伸量形变的变化曲线
2.2 分布电容分析
使用与分布电感相同的平行螺旋传输线3D模型,末端改为开路,将求解类型改为静电场,硅胶的相对介电常数为7,两导线分别配置电压激励为0 V和0.5 V,类型为标准型,设置收敛条件和求解矩阵后进行设计检查,确认无误后开始分析求解,完成后查看电容值矩阵,得到平行螺旋传输线的电容仿真结果。
根据表1的参数大小进行仿真,导程值越大代表拉伸形变量越大,修改导程值和螺旋半径,仿真得到的电容值变化曲线如图4所示,随着拉伸量的变大,导线之间的距离变大,电容值变小。
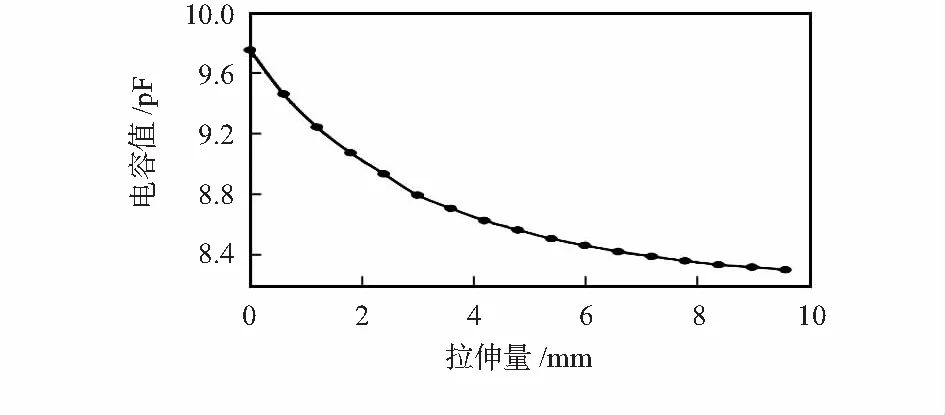
图4 分布电容值随拉伸形变量的变化曲线
2.3 特性阻抗分析
根据仿真得到的分布电感与分布电容,结合式(1)得到平行螺旋传输线的特性阻抗与导程的关系,如图5所示。

图5 特性阻抗随拉伸形变量的变化曲线
可以看出,平行螺旋传输线的特性阻抗随着拉伸形变量的变大而增大,且特性阻抗与拉伸形变量并不是简单的线性关系,而更接近于一种指数关系。将仿真得到的的特性阻抗数据拟合为指数函数Z=a×eb/x+c,其中,Z为特性阻抗,x为导程,a,b,c为待定系数,拟合结果分别为-2.3,6.431,92.59, 拟合函数的误差平方和(sum of squared error,SSE)为0.028 14,均方根误差(root-mean-square error,RMSE)为0.044 83,确定系数(R-square)为0.999 8。
3 平行螺旋传输线拉伸测量实验
实物实验前,首先要确定实验材料的参数,然后进行校准建模,以提高测量的准确性。如图6所示为有限元仿真得到的分布电容值与硅胶的相对介电常数的关系曲线,相对介电常数越大,分布电容值越大,特性阻抗就越小。
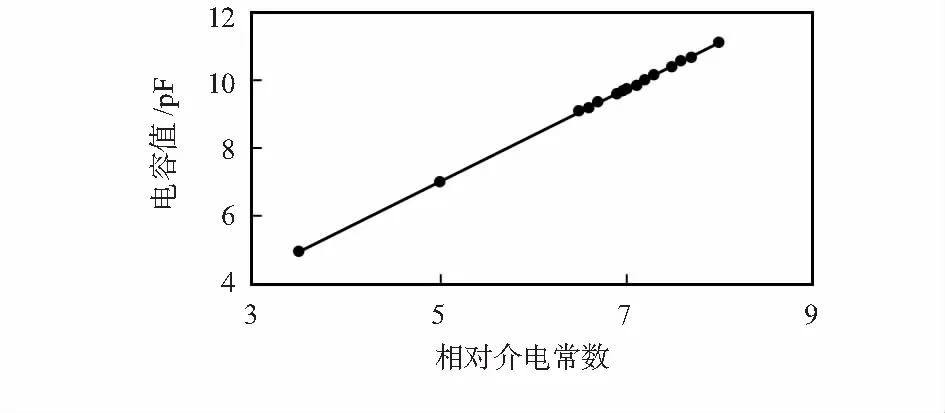
图6 分布电容随介电常数的变化曲线
图7为平行螺旋传输线拉伸形变的测量实验示意,实验的平台主要由3部分构成:拉伸平台、时域反射仪和上位机。拉伸平台用于实现平行螺旋传输线的局部拉伸,时域反射仪用于发射阶跃信号和高频采样并将采样数据上传至上位机,上位机用于对反射信号进行分析计算,得出拉伸形变的位置和大小。
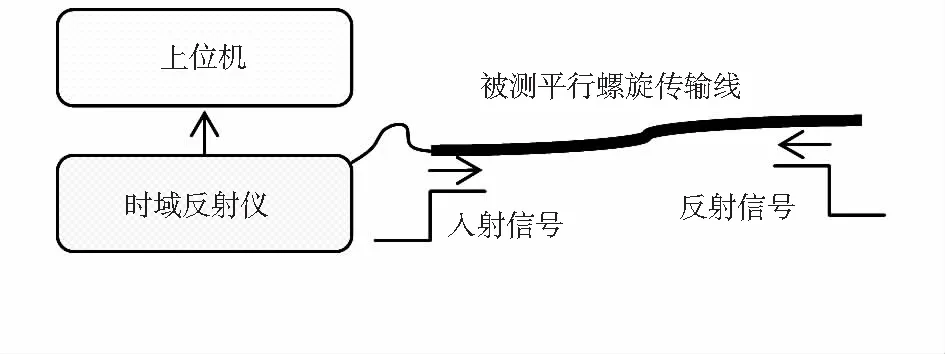
图7 拉伸测量实验示意
室温下,对一根3.6 m长平行螺旋传输线进行校准拟合实验,得到待定系数a,b,c拟合结果分别为-1.983,8.073,103, 拟合结果SSE为 0.011 86,RMSE为0.054 45,R-square为0.999 8。
对该平行螺旋传输线进行局部拉伸测量,在70~85 cm范围进行了4组不同程度的拉伸形变测量,图8为时域反射仪将测得的平行螺旋传输线被拉伸位置的特性阻抗曲线,可以看出,随着拉伸形变增大,该处特性阻抗也逐渐增大。

图8 被拉伸位置采样曲线
上位机根据拟合的指数函数模型计算出的形变量结果如表2所示。时域反射仪产生的阶越信号的上升时间和高频采样模块的采样频率是影响形变测量精度的主要因素。

表2 平行螺旋传输线拉伸形变测量结果
4 结束语
针对平行螺旋传输线的分布参数与拉伸形变量之间理论分析误差较大的问题,本文从测量方法、有限元仿真和实物实验3个方面进行了分析,得到了平行螺旋传输线的拉伸形变量与特性阻抗之间存在的指数关系,并且对实物建立了数学模型。实验结果表明:基于平行螺旋传输线的拉伸形变传感器可以应用于较大拉伸形变的分布式测量场合,且相对误差较小。

