巷道无线信道多普勒扩展及其影响因素
成凌飞, 杨 蒙, 贺 扬, 李 俊, 李飞腾
(1.河南理工大学 物理与电子信息学院, 河南 焦作 454000; 2.河南理工大学 电气工程与自动化学院, 河南 焦作 454000)
0 引 言
矿井巷道中矿井机车的使用给矿井无线通信系统带来了严重的多普勒频移问题,使接收信号的频谱结构产生不同的多普勒频移,造成多普勒扩展,增加了无线信道的衰减和接收信号的误码率,对接收机的解调性能产生较大影响。因此,有必要对多普勒频移及其影响因素进行研究来降低误码率,减小其对接收系统的性能影响。文献[1]在考虑包括井下移动平台的多普勒频移等因素的基础上,对时变多径无线信道进行仿真,得出多入多出—正交频分复用(MIMO-OFDM)技术适用于矿井巷道无线通信;文献[2]研究了当发送端移动时多普勒频移对室内定位的影响,提出了单次反射时多普勒频移公式;文献[3]在分析移动多径信道的基础上,对不同信道多普勒效应进行仿真;文献[4]利用射线分析法和无线电统计理论分析了地铁隧道环境下的无线多径信道的多普勒扩展;文献[5]在考虑到井下移动平台的造成的多普勒频移效应基础上,对2G无线电波在煤矿井下隧道传播情况进行了研究。但对于矿井巷道无线信道多普勒扩展的相关影响因素研究仍然相当缺乏。
本文在三维模型的基础上利用软件仿真对煤矿巷道无线信道的多普勒扩展进行研究,分别就移动台移动速度,载波频率以及巷道截面尺寸等对多普勒扩展的影响进行研究。
1 多普勒频移
由于移动台和基站的相对运动,引起的接收信号的频率移动称为多普勒频移。假设S为信号源,移动台正以速度v沿距离为d的路程XY运动,移动台接收信号源S发出的信号。假设信号源离得很远,来自S的电波到达目标点X和Y所产生的路径差为Δl≈dcosθ=vΔtcosθ,其中,Δt是移动台从X到Y所需要的时间。同理,在此条件下,点X和Y的到达角θ相同,则由路径差引起的信号相位变化为
(1)
式中λ为波长。则频率的视在变化即多普勒频移为
(2)
式(2)说明,移动台的移动速度和方向分别决定多普勒频移的大小和正负。移动台按照图1所示方向运动,多普勒频移为正,反之,多普勒频移为负。
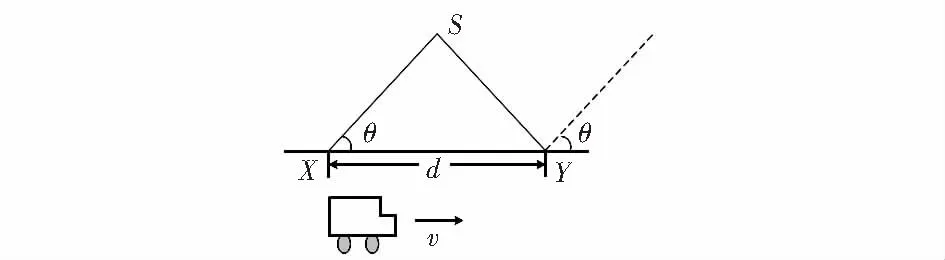
图1 多普勒效应
2 靠近基站下的多普勒频移
基站下的多普勒频移的快速变化在一定程度上容易导致设备接收信号跟不上频移变化,使得接收误差增加,最终导致误码率增加[6,7]。图2为本文研究所涉及的巷道内基站安装示意。

图2 巷道内基站安装示意
S为基站安装点,S′为基站在巷底的投影点,基站安装在巷道侧壁与巷顶的夹角处,D在Z轴上,且S′D垂直于Z轴。d为移动台相对于基站在Z轴上投影D点的直线距离,a为基站的安装高度,b为入射角θ为90°时基站在巷底的投影点S′距移动台的垂直距离(即线段S′D),其中巷道宽为w,高为h。基站下直射路径多普勒频移与移动台速度、基站到巷底的垂直距离以及基站高度的关系为
(3)
可知在移动台移动速度v为匀速的情况下,直射路径多普勒频移仅与入射角有关。而影响入射角的因素主要有4个,分别是a,b,d,v。基站投影点S′的入射角θ(t)的变化规律为
(4)
考虑到电磁波在巷道中传播时会来回反射,无线通信会产生多径效应。文献[8]分析了矩形巷道内电磁波的多径传播规律,可知除直射电磁波外,还有水平方向反射电磁波、垂直方向反射电磁波和旋进电磁波。因此,在对移动台的多普勒频移的研究中需要考虑多径传输的情况。
根据图2巷道内基站安装示意,无线信号的多径传输模型可简化为图3(a)和图3(b),巷道左、右壁和上、下顶可由平板波导简化。无线信号在水平面上传播经由左、右壁反射,设反射次数为m,其中m=1,2,3,… ;在垂直面上传播经由上、下壁反射,设反射次数为n,其中n=2,4,6,…。根据帐篷定理和镜面反射原理,经由巷道壁反射的多径信号传输路径为
(5)
式中li为第i条反射路径,当m=0,n=0时,式(5)表示直射路径。由式(2),第i条反射路径多普勒频移与移动台速度、基站到巷底的垂直距离以及基站高度的关系为
(6)

图3 反射简化图
2.1 移动台匀速运动对多普勒频移的影响
仅考虑入射角变化时,假设移动台速度分别为1,3,5 m/s,d=30 m,b=3 m,a=5 m,载波频率为900 MHz,对直射路径的多普勒频移变化进行仿真,多普勒频移变化曲线如图 4 (a)。可知,当移动台刚进入基站范围时(t=0 s,入射角θ≈0°),直射路径的多普勒频移达到正最大;当移动台沿Z轴正方向移动,经过基站至巷底的投影时,θ=90°,直射路径多普勒频移为0 Hz;当移动台继续移动,即将离开基站覆盖范围时(θ≈180°),直射路径的多普勒频移达到负最大值。同时,当多普勒频移大于0 Hz时,可知移动台接近基站;多普勒频移小于0 Hz时,可知移动台远离基站;由此可以得出,多普勒频移在0 Hz值附近变化最快,且当移动台速度越快,多普勒频移变化越快。
反射路径多普勒频移变化曲线如图4(b)所示。本文仿真只考虑有限次反射,反射次数1≤k≤3,k=m+n。

图4 匀速时多普勒频移变化曲线
由图4(b)可知,信号反射次数越多,多普勒频移越小,且每条反射路径的多普勒频移随速度变化规律与直射路径相同。对比两图可知,速度对无线信号多普勒频移的影响大于反射次数对其多普勒频移的影响。
2.2 巷道截面尺寸对多普勒频移的影响
2.2.1 巷道高度对多普勒频移的影响
假设移动台的移动速度为3 m/s,基站在巷底的投影到巷道中心的距离为3 m,即b=3 m,载波频率为900 MHz,天线高度分别为2,5,8 m,在这种假设情况下对巷道高度,也就是基站的安装高度对直射路径多普勒频移的影响进行仿真,如图5(a)所示。巷道高度对反射路径多普勒频移的影响仿真,如图5(b)所示。

图5 巷道高度对多普勒频移的影响
由图5(a)可以看出,在可视范围内直射路径多普勒频移变化与基站高度成反比:基站高度越高,多普勒频移变化越缓慢;反之,基站高度越低,多普勒频移变化越剧烈。由图5(b)可以看出,在反射次数相同的情况下,巷道高度较低时,在垂直面反射次数越多的反射路径多普勒频移较大;巷道高度较高时,在垂直面反射次数较少的反射路径多普勒频移较大。在垂直面反射次数相同的情况下,水平面反射次数越多,多普勒频移越小。同时,每条反射路径的多普勒频移变化规律与直射路径相同。
2.2.2 巷道宽度对多普勒频移的影响
假设移动台始终沿着巷道中心线移动,即b=w/2,巷道高度为5 m,即基站安装高度为5 m,移动台移动速度为3 m/s,载波频率为900 MHz,分别对巷道宽w为4,8,12 m的情况进行仿真,直射路径仿真结果如图6(a)所示。巷道宽度对反射路径多普勒频移的影响仿真,如图6(b)所示。

图6 巷道宽度对多普勒频移的影响
由图 6(a)可以看出,在可视范围内直射路径多普勒频移变化与巷道宽度成反比;巷道越宽,多普勒频移变化越缓慢;反之,巷道越窄,多普勒频移变化越剧烈。由此可以看出截面尺寸越大,多普勒频移越缓慢。反之截面尺寸越小,多普勒频移变化越剧烈。由图6(b)可知,在反射次数相同的情况下,巷道较窄时,在水平面反射次数越多的反射路径多普勒频移较大;巷道较宽时,在水平面反射次数较少的反射路径多普勒频移较大。在水平面反射次数相同的情况下,垂直面反射次数越多,多普勒频移越小。同时,每条反射路径的多普勒频移变化规律与直射路径相同。
2.3 载波频率对多普勒频移的影响
假设移动台始终沿着巷道中心线移动,巷道宽6 m,也就是移动台离巷壁距离为3 m,巷道高度为5 m也就是基站安装高度为5 m,移动台移动速度为3 m/s,对载波频率为600,900,1 200,1 800 MHz的情况进行仿真,直射路径仿真结果如图7(a)所示。载波频率对反射路径路多普勒频移的影响仿真,如图7(b)所示。

图7 载波频率对多普勒频移的影响
由图7(a)可以看出,在可视范围内直射路径多普勒频移变化与载波频率成正比:载波频率越高多普勒频移越大,在接近基站时变化越陡峭。这是因为随着频率的增加时延扩展越小的原因。由图7(b)可知,信号反射次数越多,多普勒频移越小,且每条反射路径的多普勒频移与载波频率的关系与直射路径情况下相同。
3 结 论
在影响多普勒扩展的因素中,移动台的速度和载波频率对多普勒频移影响较大,而巷道截面尺寸、多径传输信号在巷道内的反射次数对多普勒频移影响较小。

