基于摄影测量学和图像光流的三维重建方法*

黄会明, 郭 进， 段康容

(1．西南财经大学 天府学院，四川 绵阳 621000； 2．四川大学 电子信息学院，四川 成都 610065)

0 引 言

传统的三维(3D)测量方式在满足高精度和高质量的要求方面，具有一定的局限性，如不便携带、需要很多辅助设备、无法快速方便获得物体纹理信息等，如Breuckman B等人[1]提出的相位轮廓技术,需要工业相机和投影设备辅助进行；His-Yung Fenga等人[2]提出的基于线激光三维重建方法,也需要工业相机和激光发射设备等。上述方法均只能获取到小范围物体的三维数据，且辅助设备价格昂贵，需要专门的操作技术人员。

基于近景摄影测量学和光流[3]的三维测量方式恰好满足了上述需求。本文采用这种测量方式，只需用一台单反相机对物体从不同角度拍摄多幅图片获取三维信息。使用一些人工的标记点通过自标定的方法标定相机的内参数；拍摄需要重建的物体图像，通过物体自身的特征点，如SIFT特征信息[4]，完成相机的外参数的标定；利用光流检测算法计算出不同角度拍摄的两幅图像中每个像素点的光流值；基于两幅图像光流场的变化值获得像素精度的匹配点，根据匹配点和相机的标定数据重建出物体的三维信息。

1 相机标定

1.1 内参数标定

对内参数的标定采用自标定算法[5]，首先进行射影重建，经过仿射变换后可以将射影重建转换到射影空间下，最后用欧氏变换将仿射空间转换到欧氏空间下从而实现欧氏三维重建[6]。

根据针孔相机模型的成像原理，在理想的情况下拍摄到的图像点与镜头中心和物体三维点具有三点共线性，根据这个特性，可以使用齐次坐标矩阵表示

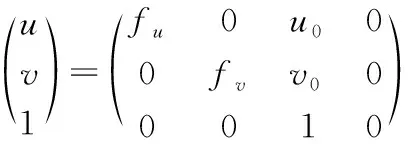
(1)

式中 (u,v)为图像的二维坐标,fu和fv分别为相机在图像的横轴和纵轴上的基于像素的焦距,(u0,v0)为图像的中心点坐标,R和T分别为相机坐标到世界坐标的转换关系，即两个坐标系的旋转和平移向量,(X,Y,Z)为物体在世界坐标系下的三维坐标。

实际上空间三维点到图像二维点的成像过程中存在一定的偏差，可以表示为(Δu,Δv)。另外,相机在生产的过程中是存在一定的加工误差，形成了相机的光学畸变，可以将这种畸变加入到相机的模型中去，将共线方程改写为

(2)

(3)

为避免图像在采集过程中出现误差，采用了基于光束法平差的方法对相机的内参数、外参数和空间三维坐标捆绑一起进行非线性优化[7,8]。根据最小二乘的原理，将优化的目标函数设置为

(4)

利用目标函数，对式(3)使用泰勒公式进行展开，并取其一阶项，结果中图像二维坐标(u,v)在实际成像过程中会存在一定的误差，加入一个改正数(vu,vv)，即

u+vu=(u)+du,v+vv=(v)+dv

(5)

获得摄影测量中的误差方程，其矩阵形式为

(6)

式中 矩阵B和矩阵C分别为图像中的二维点对相机内外参数的偏导数和图像二维点对物体三维点的偏导数；矩阵δp和矩阵δt均为改正数，即相机内外参数的改正数和物体三维点的改正数；矩阵L为图像观测值。通过优化式(6)就可以计算出相机的内参数矩阵。

1.2 外参数标定

在双视图重建中，外参数的标定一般采用基于本质矩阵E进行，假设一对归一化后的相机矩阵P=[I0]和P′=[R′T]，与归一化相机矩阵对应的基础矩阵即为本质矩阵[10]，包括了两个相机之间的相对空间位置信息，具体形式为

E=[T]×R

(7)

式中 [T]×为平移向量的反对称矩阵。E通过奇异值分解(singular value decomposition,SVD)为Udiag(1,1,0)VT，第一个相机投影矩阵为P=[I0]，第二个相机的投影矩阵P′具有如下4种可能选择

P′=[UWVT|u3];[UWVT|-u3];

[UWTVT|u3];[UWTVT|-u3]

(8)

外参数的标定可以使用5点法[9]进行计算，首先在两幅图像上使用SIFT特征提取方法，获取到两张图片大于5个匹配的二维图像点，使用匹配点可以计算出两个相机的外参数。

2 图像光流计算

依据三维物体上的一个点在两幅图像上具有旋转位移不变性[11,12]，将光流定义为从不同角度拍摄的物体产生的矢量场。设一个图像二维点坐标为(x,y),可以表示为空间中某一个三维点(X,Y,Z)在图像上投影的二维坐标，并且该图像点在时刻t对应的图像灰度信息为I(x,y,t)。设在一个很短的时间内即t+Δt时图像点发生了一定的位移，即从(x,y)处运动了(u,v)的距离,到达点(x+u,y+v)处,若在很短的时间Δt内图像点从一点运动到另外一点,认为图像点对应的图像灰度值保存不变。

设I∶Ω⊂R3→R表示图像序列，w=(u,v,1)就是时间t,t+1时刻图像的位移矢量。灰度值不变假设有一个决定性的缺点：对自然场景中的亮度的微小变化很敏感。因此，在灰度值上允许一些小的变化，有助于确定一个标准，在这个标准下当图像之间产生了位移矢量也不会引起其值的变化，即图像梯度

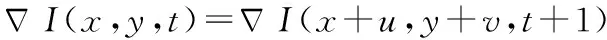
(9)

在计算单个像素的位移矢量时需要考虑到周围像素的贡献值,在估计某个像素的光流场时假设在不同的时刻图像的平滑度一致，且可以采用多分辨率的方法逐步实现。最后使光流场的函数在某一局部位置收敛到最小。

从上述2种假设中可以设置一个能量函数E1(u,v)，包含了图像的灰度信息和梯度信息，即

E1(u,v)=

(10)

式中X=(x,y,t)T,W=(u,v,1)T，λ为假设两者之间的权重。

对于图像多分辨率的光滑数学模型，可以通过定义图像梯度场能量函数E2(u,v)来实现，对二维像素坐标和时间分别求偏导，即

E2(u,v)=

(11)

对于两幅图片求光流矢量(u,v)的应用中，总能量函数是能量函数E1(u,v)和E2(u,v)的加权和

E(u,v)=E1(u,v)+δE2(u,v),δ>0

(12)

使能量函数M达到最小的(u,v)即为所求的两幅图像之间的像素点的位移矢量。

3 三维重建

三维重建主要依据三角测量原理，已知不同位置的两幅图像上的一组对应点m1,m2，其与各自相机的光心连线o1m1,o2m2必定交于空间一点M，此点即为此组对应点的空间物点，如图1所示。

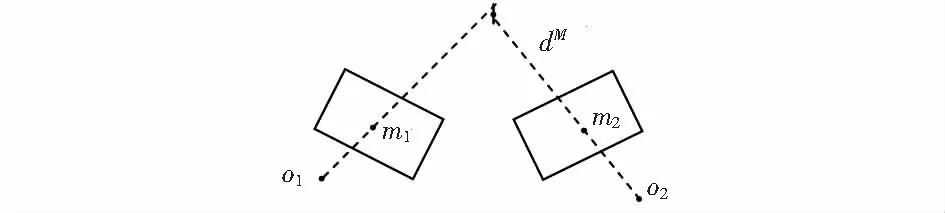
图1 三角测量原理

根据光流计算方法可以很容易地找到两幅图片上的匹配点，如第一副图片上一个像素点为m1=(u1,v1,1)，计算的位移矢量为w=(u,v,1)，则另一幅图片上的匹配点为

m2=(u2,v2,1)=(u1+u,v1+v,1)

(13)

两个相机的投影矩阵分别表示为P1=K1[P1T1],P2=K2[R2T2]，根据透视投影公式可得

(14)

式中λ1，λ2为非零比例因子,消去后，整理为矩阵形式

(15)

依据最小二乘原理即可求出三维点的坐即

X=(ATA)-1ATb

(16)

4 实验结果

实验过程只需要使用一台单反相机，焦距35 mm，相机分辨率1 024×1 280。拍摄距离5 m，视场大小4 m×5 m。

图2 编码标记点

图3 假山图像SIFT点匹配

3)光流计算方法计算两幅图像上的光流场：根据光流场来对像素级别的稠密点进行匹配，可以得到两幅图像上稠密的二维图像匹配点。根据三角测量原理，利用内参和外参以及图像上的匹配点进行三维点的重建，并获取到每个三维点对应的图像颜色值。重建的效果如图4和图5。

图4 假山三维数据

图5 石壁三维数据

5 结 论

本文创新地在摄影测量原理基础上使用光流来替代图像点的匹配，只需采集几张图像即可重建出物体的稠密点三维信息。避免了传统方法使用额外的辅助设备，此方法可以方便地用于3D打印和虚拟现实的三维数据获取中。